Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the full QR decomposition of a matrix
ResourceFunction["FullQRDecomposition"][m] yields the full QR decomposition for a numerical matrix m. The result is a list {q,r}, where q is a unitary matrix and r is an upper‐trapezoidal matrix. |
Compute the full QR decomposition for a 3×2 matrix with exact values:
| In[1]:= |
| Out[1]= |
| In[2]:= |
| Out[2]= | 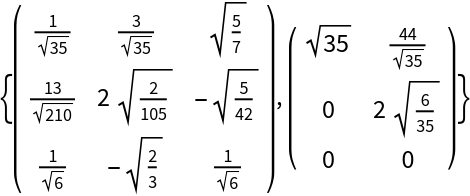 |
Compute the full QR decomposition for a 2×3 matrix with approximate numerical values:
| In[3]:= |
| Out[3]= |
| In[4]:= |
| Out[4]= |
Use a 3×4 matrix:

Full QR decomposition computed with exact arithmetic:
| In[5]:= |
| Out[5]= | 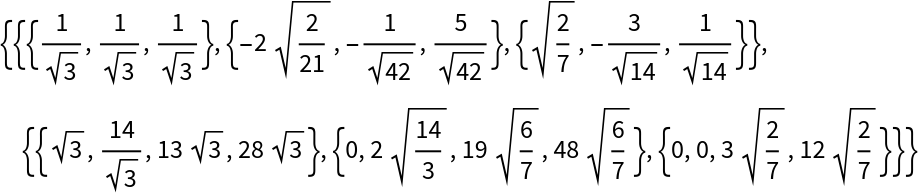 |
Full QR decomposition computed with machine arithmetic:
| In[6]:= |
| Out[6]= |
| In[7]:= |
| Out[7]= |
Full QR decomposition computed with 24-digit arithmetic:
| In[8]:= |
| Out[8]= |  |
Full QR decomposition for a 3×3 matrix with random complex entries:
| In[9]:= |
| Out[9]= |  |
| In[10]:= |
| Out[10]= |  |
Use a 3×4 matrix:

Compute the full QR decomposition using machine arithmetic with pivoting:
| In[11]:= |
| Out[11]= |  |
The elements along the diagonal of r are in order of decreasing magnitude:
| In[12]:= |
| Out[12]= |
The matrix p is a permutation matrix:
| In[13]:= |
| Out[13]= | 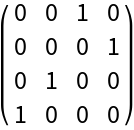 |
FullQRDecomposition satisfies m.p==ConjugateTranspose[q].r:
| In[14]:= |
| Out[14]= |
Here is some data:
| In[15]:= | ![times = {1., 2., 3., 4., .5};
b = {5., 2., 3., 6., 10.};
data = Transpose[{times, b}];](https://www.wolframcloud.com/obj/resourcesystem/images/137/1374d83f-2048-4f09-aec6-e4f812e00f0b/6c48e53b6dc9ac03.png) |
| In[16]:= |
| Out[16]= | 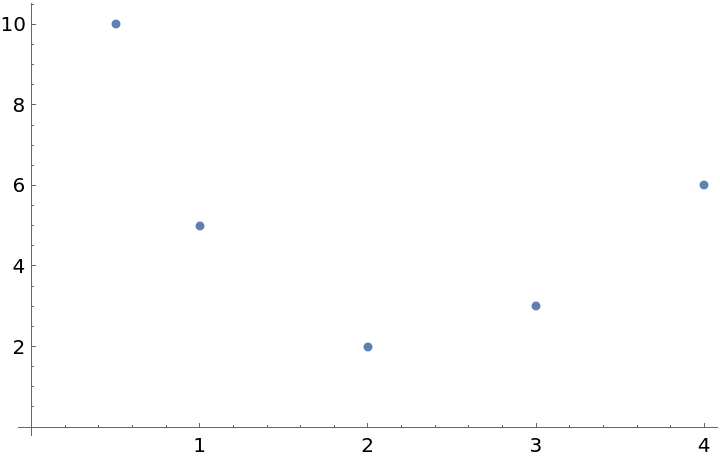 |
Set up a design matrix for fitting with basis functions 1, t, t2:
| In[17]:= |
| Out[17]= |
Find the full QR decomposition of m:
| In[18]:= |
| Out[18]= |  |
This finds a vector x such that ![]() is a minimum:
is a minimum:
| In[19]:= |
| Out[19]= |
These are the coefficients for the least-squares fit:
| In[20]:= |
| Out[20]= |
| In[21]:= |
| Out[21]= | 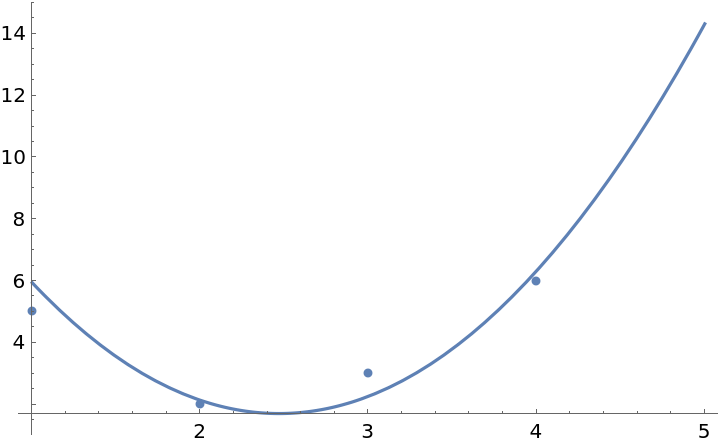 |
Use a 3×4 matrix:
| In[22]:= | ![m = \!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{"1", "2", "3", "4"},
{"1", "4", "9", "16"},
{"1", "8", "27", "64"}
},
GridBoxAlignment->{"Columns" -> {{Left}}, "ColumnsIndexed" -> {}, "Rows" -> {{Baseline}}, "RowsIndexed" -> {}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}, "RowsIndexed" -> {}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\);](https://www.wolframcloud.com/obj/resourcesystem/images/137/1374d83f-2048-4f09-aec6-e4f812e00f0b/72481de52a79d41a.png) |
Compute the full QR decomposition:
| In[23]:= |
The rows and columns of q are orthonormal:
| In[24]:= |
| Out[24]= |
| In[25]:= |
| Out[25]= |
Check that r is upper trapezoidal:
| In[26]:= |
| Out[26]= |
| In[27]:= |
| Out[27]= |
| In[28]:= |
| Out[28]= |
Check that m is equal to ConjugateTranspose[q].r:
| In[29]:= |
| Out[29]= |
This work is licensed under a Creative Commons Attribution 4.0 International License