Wolfram Research

Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 FubiniNumber (1.0.0) current version: 1.0.1 »

Source Notebook

Count the number of ways to partition a set where the order of the subsets matters

Contributed by: George Beck

ResourceFunction["FubiniNumber"][set]

counts the number of ways to partition set into subsets, where the order of the subsets matters.

Examples

Basic Examples

The simplest non-trivial Fubini number:

In[1]:=
ResourceFunction["FubiniNumber"][2]
Out[1]=

Here are the first 10 Fubini numbers:

In[2]:=
ResourceFunction["FubiniNumber"] /@ Range[10]
Out[2]=

Scope

This shows the 13 ordered set partitions of the the set {1,2,3}:

In[3]:=
partitions = Apply[Join, Permutations /@ ResourceFunction["SetPartitions"][{1, 2, 3}]]; % // Column
Out[4]=
In[5]:=
Length@partitions
Out[5]=

This accords with:

In[6]:=
ResourceFunction["FubiniNumber"][3]
Out[6]=

Neat Examples

The Fubini numbers are periodic mod 10:

In[7]:=
ListLinePlot@ Table[Mod[ResourceFunction["FubiniNumber"][n], 10], {n, 20}]
Out[7]=

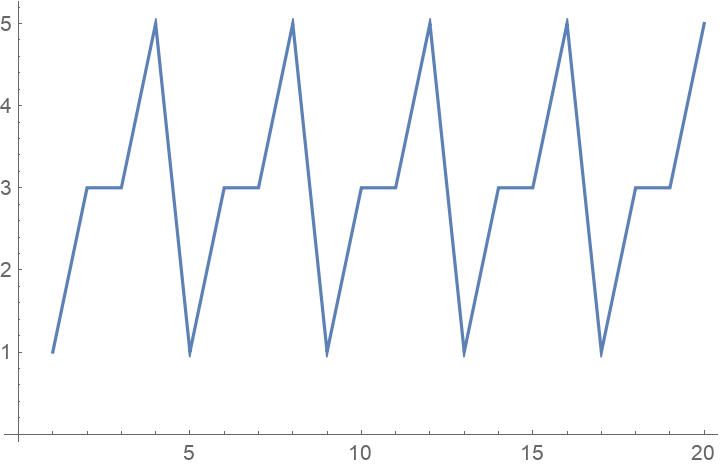
There are many other modular relations:

In[8]:=
ListLinePlot@ Table[Mod[ResourceFunction["FubiniNumber"][n], 11], {n, 20}]
Out[8]=

Requirements

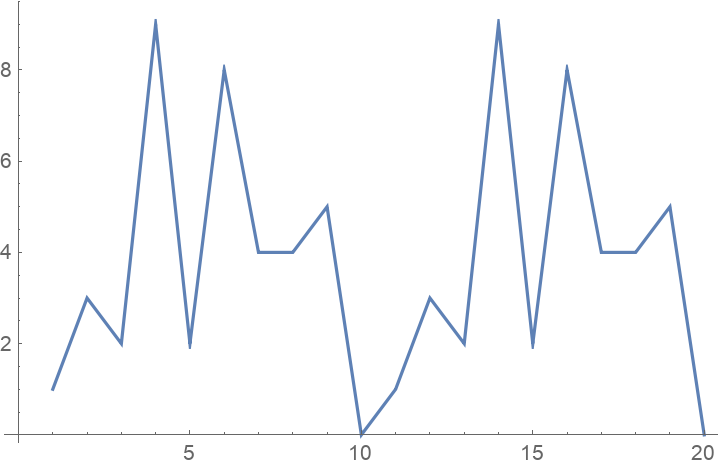
Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.0.1 – 07 February 2022
  • 1.0.0 – 10 May 2019

License Information