Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 FubiniNumber

Source Notebook

Count the number of ways to partition a set where the order of the subsets matters

Contributed by: George Beck

ResourceFunction["FubiniNumber"][n]

counts the number of ways to partition a set of length n into subsets, where the order of the subsets matters.

Examples

Basic Examples (2) 

The simplest non-trivial Fubini number:

In[1]:=
ResourceFunction["FubiniNumber"][2]
Out[1]=

Here are the first 10 Fubini numbers:

In[2]:=
ResourceFunction["FubiniNumber"][Range[10]]
Out[2]=

Scope (2) 

This shows the 13 ordered set partitions of the the set {1,2,3}:

In[3]:=
Column[partitions = Apply[Join, Permutations /@ ResourceFunction["SetPartitions"][{1, 2, 3}]]]
Out[3]=
In[4]:=
Length[partitions]
Out[4]=

Use FubiniNumber to get the same result:

In[5]:=
ResourceFunction["FubiniNumber"][3]
Out[5]=

Neat Examples (2) 

The Fubini numbers are periodic mod 10:

In[6]:=
ListLinePlot[ Table[Mod[ResourceFunction["FubiniNumber"][n], 10], {n, 20}]]
Out[6]=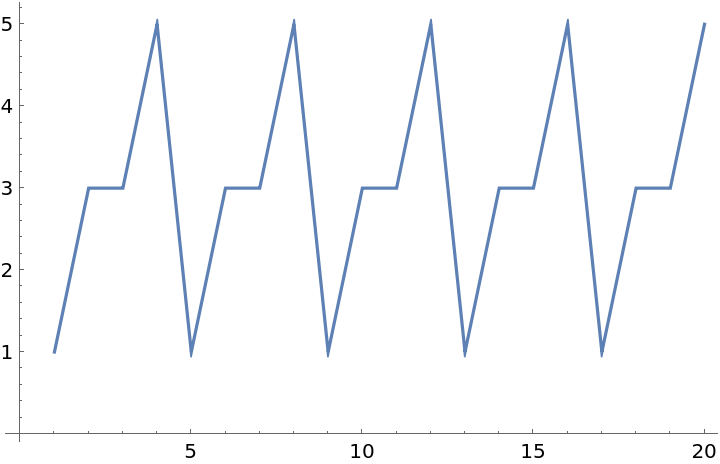

There are many other modular relations:

In[7]:=
ListLinePlot[ Table[Mod[ResourceFunction["FubiniNumber"][n], 11], {n, 20}]]
Out[7]=

Publisher

George Beck

Requirements

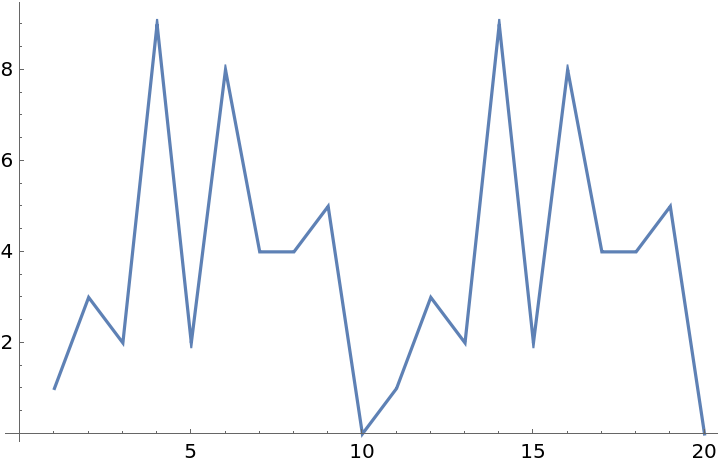Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.0.1 – 07 February 2022
  • 1.0.0 – 10 May 2019

Related Resources

License Information