Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 FrobeniusSymbolFromPartition

Source Notebook

Get a pair of lists representing the Ferrers diagram of a partition

Contributed by: George Beck

ResourceFunction["FrobeniusSymbolFromPartition"][λ]

gives a pair of lists that count dots in the rows and columns relative to the diagonal of the Durfee square in the Ferrers diagram of the partition λ.

Details and Options

A partition of n is a list of weakly decreasing positive integers that add up to n. For instance, written compactly, these are the five partitions of 4: 4, 31, 22, 211, 1111.
In the output of ResourceFunction["FrobeniusSymbolFromPartition"], the first list represents the number of dots to the right of the diagonal in the Ferrers diagram of the given partition, and the second list represents the number of dots below the diagonal.

Examples

Basic Examples (4) 

Compute the Frobenius symbol of a partition:

In[1]:=
ResourceFunction["FrobeniusSymbolFromPartition"][{7, 7, 4, 2, 1}]
Out[1]=

Here we use a partition of 8 consisting of only one large part:

In[2]:=
ResourceFunction["FrobeniusSymbolFromPartition"][{8}]
Out[2]=

Here the partition is 11111111, with many small parts:

In[3]:=
ResourceFunction[ "FrobeniusSymbolFromPartition"][{1, 1, 1, 1, 1, 1, 1, 1}]
Out[3]=

Here is an intermediate case:

In[4]:=
ResourceFunction[ "FrobeniusSymbolFromPartition"][{7, 6, 5, 4, 3, 2, 1}]
Out[4]=

Scope (4) 

A partition is a list of nonincreasing positive integers:

In[5]:=
\[Lambda]1 = {7, 7, 4, 2, 1};

Here is its Ferrers diagram:

In[6]:=
Framed@Grid[Table["\[FilledCircle]", #] & /@ \[Lambda]1]
Out[6]=

Define a partition:

In[7]:=
part = {7, 7, 4, 2, 1};

Here is the result of applying FrobeniusSymbolFromPartition to the partition:

In[8]:=
ResourceFunction["FrobeniusSymbolFromPartition"]@part
Out[8]=

Now, define a function to illustrate the definition of the Frobenius symbol:

In[9]:=
FrobeniusSymbolFromPartitionGrid@\[Lambda]_ := Module[ {x, r}, x = ResourceFunction["FrobeniusSymbolFromPartition"][\[Lambda]]; r = Range@Length@First@x; Text@Grid[ Transpose@Append[ Transpose[ PadRight@ Append[ ReplacePart[Table["\[FilledCircle]", #] & /@ \[Lambda], Transpose@{r, r} -> "\[EmptyCircle]"], ToString /@ x[[2]] ] ], PadRight[ToString /@ x[[1]], 1 + Length@\[Lambda]] ] ]] /. 0 -> ""

Apply the function to the partition:

In[10]:=
FrobeniusSymbolFromPartitionGrid@part
Out[10]=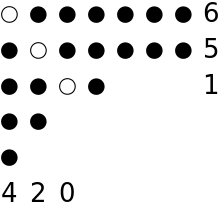

The output indicates that the number of dots in the rows to the right of the diagonal is 6, 5, 1 while the number of dots in the columns below the diagonal is 4, 2, 0.

These lists are the rows of the Frobenius symbol of the partition:

In[11]:=
ResourceFunction["FrobeniusSymbolFromPartition"][{7, 7, 4, 2, 1}]
Out[11]=

Here is another example:

In[12]:=
\[Lambda]2 = {8, 7, 5, 4, 2, 2};
In[13]:=
FrobeniusSymbolFromPartitionGrid@\[Lambda]2
Out[13]=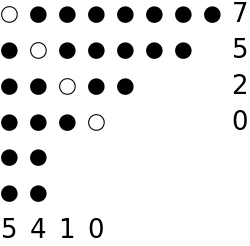
In[14]:=
ResourceFunction["FrobeniusSymbolFromPartition"]@\[Lambda]2
Out[14]=

Properties and Relations (1) 

Confirm that Frobenius symbols and partitions round trip as expected:

In[15]:=
\[Lambda]1 = {7, 7, 4, 2, 1}; \[Lambda]2 = {8, 7, 5, 4, 2, 2};
In[16]:=
\[Lambda]1 == ResourceFunction["PartitionFromFrobeniusSymbol"]@ ResourceFunction["FrobeniusSymbolFromPartition"]@\[Lambda]1
Out[16]=
In[17]:=
\[Lambda]2 == ResourceFunction["PartitionFromFrobeniusSymbol"]@ ResourceFunction["FrobeniusSymbolFromPartition"]@\[Lambda]2
Out[17]=

Publisher

George Beck

Requirements

Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.0.0 – 10 May 2019

Source Metadata

  • Citation:
    • Andrews, G. E. Eriksson, K., Integer Partitions, pg. 78. Cambridge: Cambridge University Press, 2004.

Related Resources

License Information