Function Repository Resource:

Fractran

Source Notebook

Interpret the FRACTRAN esoteric programming language

Contributed by: Daniel Sanchez and Jan Mangaldan

ResourceFunction["Fractran"][prog,n]

runs the FRACTRAN program prog on the integer n.

Details and Options

FRACTRAN is an esoteric programming language invented by the mathematician John H. Conway.

The result of a FRACTRAN execution is a list of integers.

A FRACTRAN program can have one of the following forms:

FRACTRAN-1 program

{f₁,f₂,…}

where each f_i is a positive fraction

FRACTRAN-n program

{…,{f_l₁→l₁,f_l₂→l₂,…},…}

where f_{l_m} are positive fractions and each l_m is an integer between 1 and n (the length of the list)

The FRACTRAN-1 program ResourceFunction["Fractran"][{f₁,f₂,…,f_i,…},n] repeatedly multiplies the integer at any stage (initially n) against the earliest fraction f_i in the list that yields an integer product, stopping the execution when there is no such f_i.

The FRACTRAN-n program ResourceFunction["Fractran"][{…,{f_l₁→l₁,f_l₂→l₂,…},…},n] repeatedly multiplies the integer at any stage (initially n) against the earliest fraction f_{l_m} in line l (initially 1) that yields an integer product, then proceeds to the line indicated by l_m, stopping the execution when there is no such f_{l_m}.

The first element of the resulting list is always the starting integer n.

If ResourceFunction["Fractran"] terminates early, the last element of the resulting list is 0.

ResourceFunction["Fractran"] has the following options:

MaxIterations

Infinity

maximum number of iterations

"MaxResults"

Infinity

maximum number of integers in the result

"SelectionCriterion"

Automatic

test to determine whether an integer should be included in the result

"ShowProgramLines"

False

if set to True, show the program line currently being executed

The FRACTRAN language can be considered a type of register machine where: 1) The integer n stores the contents of the registers in the exponents of prime factors of n. For example 34992 = 2⁴×3⁷ represents a register state in which the register "2" holds the value 4 and the register "3" the value 7. 2) Each positive fraction f_i in a program represents an instruction that operates on the integer n. The instruction is executed only if f_i × n yields an integer product, otherwise, a negative value will be stored in the register state n. For example, the fraction

can operate on 2⁴×3⁷ resulting in 2³×3⁸, but not on 3¹¹ as the final register state would be 2^-1×3¹².

Examples

Basic Examples (3)

Run a simple FRACTRAN program representing integer addition, where given an input of the form 2^a3^b the program will have a + b encoded as 3^a+b in the last positive integer of the resulting list:

In[1]:=

$ResourceFunction["Fractran"][{3/2}, 2^4 3^7]$

Out[1]=

Decode the answer:

In[2]:=

Out[2]=

The following program represents integer subtraction, where given the input of the form 2^a3^b the program will have a - b encoded as 2^a-b (for a>b) in the last positive integer of the resulting list:

In[3]:=

$Function[{a, b}, BitLength[ResourceFunction["Fractran"][{1/(2 3)}, 2^a 3^b][[-2]]] - 1][20, 18]$

Out[3]=

Use John Conway's PRIMEGAME program to compute prime numbers encoded as powers of 2 if the program is started at 2:

In[4]:=

primeGame = {17/91, 78/85, 19/51, 23/38, 29/33, 77/29, 95/23, 77/19, 1/17, 11/13, 13/11, 15/2, 1/7, 55};
Log2@Rest@
ResourceFunction["Fractran"][primeGame, 2, MaxResults -> 10, SelectionCriterion -> IntegerQ@*Log2]

Out[64]=

In[65]:=

Out[65]=

Scope (2)

FRACTRAN-1 program (1)

Define addition by using the FRACTRAN-1 program:

In[66]:=

$fractranAddition[a_, b_] := Log[3, ResourceFunction["Fractran"][{3/2}, 2^a 3^b][[-2]]] Table[{StringTemplate["`1` + `2` = `3`"][a, b, fractranAddition[a, b]]}, {a, 5, 10}, {b, 10, 15}] // TableForm$

Out[67]=

FRACTRAN-n program (1)

The following FRACTRAN-n program corresponds to multiplication, where given the input of the form 3^a7^b the program will stop when 2^{a b} is computed:

In[68]:=

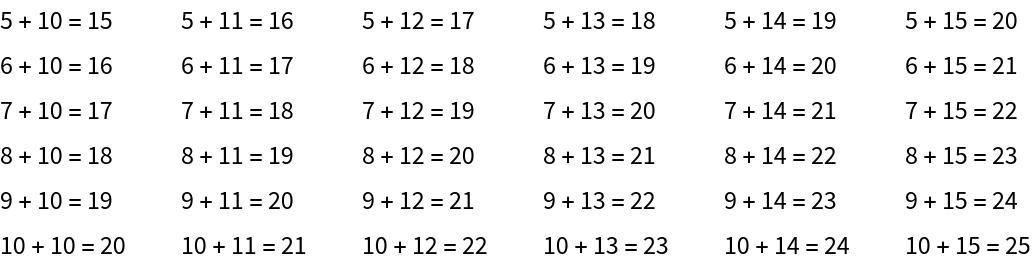
$multiplicationProgram = { {1/7 -> 2, 1/3 -> 1}, (* decrement the contents of Subscript[r, 7] by 1 and jump to line 2; clear Subscript[r, 3] *) {(5 2)/3 -> 2, 1/1 -> 3}, (* move the contents of Subscript[r, 3] to Subscript[r, 2] and Subscript[r, 5]; jump to line 3 *) {3/5 -> 3, 1/1 -> 1}}; (* restore the contents of Subscript[r, 3] from Subscript[r, 5]; loop back to line 1 *) fractranMultiplication[a_, b_] := Log2@ResourceFunction["Fractran"][multiplicationProgram, 3^a 7^b][[-2]] Table[{StringTemplate["`1` * `2` = `3`"][a, b, fractranMultiplication[a, b]]}, {a, 5, 10}, {b, 10, 15}] // TableForm$

Out[69]=

Options (6)

MaxIterations (1)

MaxIterations specifies the maximum number of steps to take in running the Fractran program:

In[70]:=

Out[70]=

MaxResults (2)

"MaxResults" specifies the maximum number of integers to be returned, excluding the initial condition:

In[71]:=

Out[72]=

This option is most commonly used with "SelectionCriterion":

In[73]:=

Out[74]=

SelectionCriterion (1)

For "SelectionCriterion" → crit, all integers n_i of the resulting list for which crit[n_i] is True are picked:

In[75]:=

Out[76]=

ShowProgramLines (2)

If "ShowProgramLines" set to True, append the program line currently being executed:

In[77]:=

$ResourceFunction[ "Fractran"][{{Rational[1, 7] -> 2, Rational[1, 3] -> 1}, {Rational[10, 3] -> 2, 1 -> 3}, {Rational[3, 5] -> 3, 1 -> 1}}, 3^5 7^4, ShowProgramLines -> True]$

Out[77]=

This option is mainly used alongside FRACTRAN-n programs. For FRACTRAN-1 programs, the line shown is always 1:

In[78]:=

$ResourceFunction["Fractran"][{1/(2 3)}, 2^8 3^3, ShowProgramLines -> True]$

Out[78]=

Possible Issues (1)

The default value of the MaxIterations is Infinity and as such, special care should be taken when the Fractran program does not halt:

In[79]:=

Out[79]=

Neat Examples (2)

Kilminster's prime number generator:

In[80]:=

primeKilminster = {3/11, 847/45, 143/6, 7/3, 10/91, 3/7, 36/325, 1/2, 36/5};
ResourceFunction["Fractran"][primeKilminster, 10, SelectionCriterion -> IntegerQ@*Log10, MaxResults -> 10]

Out[81]=

Use IntegerLength to get the result:

In[82]:=

Out[82]=

Calculate the Hamming weight H[a] of the binary expansion of a, where if given the input 2^a its output is 13^H[a]:

In[83]:=

$hammingDistance = {(3 11)/(2^2 5), 5/11, 13/(2 5), 1/5, 2/3, (2 5)/7, 7/2}; fracHammingWeight[a_Integer] := Log[13, ResourceFunction["Fractran"][hammingDistance, 2^a][[-2]]] fracHammingWeight[29]$

Out[84]=

Compare it with a custom Hamming weight defined in terms of HammingDistance:

In[85]:=

$wlHammingWeight[a_Integer] := HammingDistance[IntegerDigits[a, 2], ConstantArray[0, IntegerLength[a, 2]]] And @@ Table[fracHammingWeight[i] === wlHammingWeight[i], {i, 1, 32}]$

Out[86]=

Publisher

Daniel Sanchez

Requirements

Wolfram Language 12.2 (December 2020) or above

Version History

1.0.0 – 18 January 2021

Source Metadata

Citation:
- Conway, J.H., "FRACTRAN: A Simple Universal Programming Language for Arithmetic." In: Cover, T.M., Gopinath, B. (eds), Open Problems in Communication and Computation. New York: Springer, 1987. DOI: 10.1007/978-1-4612-4808-8_2
- Conway, J.H., Hsu, T., "Some very interesting sequences." In: Shubin, T., Hayes, D.F., Alexanderson, G. (eds.), Expeditions in Mathematics, 75-86. Washington, D.C.: Mathematical Association of America, 2011. http://www.math.sjsu.edu/~hsu/pdf/sequences.pdf

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License

Wolfram Function Repository

Fractran

Details and Options