Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the fractional derivative of an expression
ResourceFunction["FractionalOrderD"][f,{x,α}] gives the α-order fractional integro-derivative of f with respect to x. |
Compute a fractional derivative of a power function:
| In[1]:= |
| Out[1]= |
The first-order fractional derivative is equivalent to differentiation:
| In[2]:= |
| Out[2]= |
| In[3]:= |
| Out[3]= |
The negative-first-order fractional derivative is equivalent to indefinite integration:
| In[4]:= |
| Out[4]= |
| In[5]:= |
| Out[5]= |
Compute the fractional derivative of symbolic order α of an exponential function:
| In[6]:= |
| Out[6]= |
Compute the fractional derivative of symbolic order α of a logarithmic function:
| In[7]:= |
| Out[7]= |
FractionalOrderD works for both numeric and symbolic orders:
| In[8]:= |
| Out[8]= |  |
| In[9]:= |
| Out[9]= | 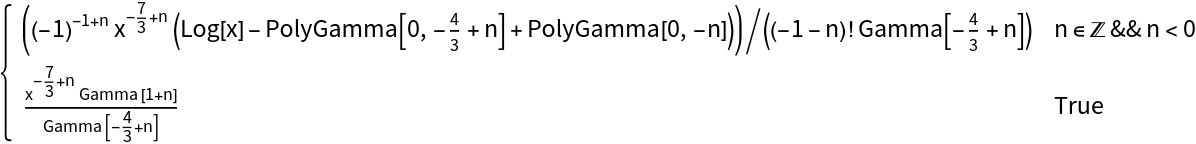 |
FractionalOrderD may return results in terms of inactivated symbols like Sum, Product, Table, MeijerG, etc:
| In[10]:= |
| Out[10]= | 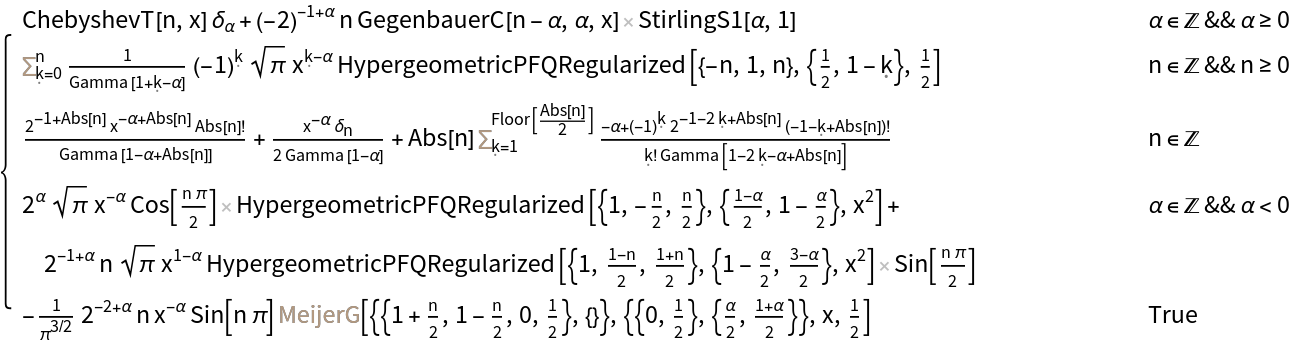 |
| In[11]:= |
| Out[11]= |
In order to use such expressions, first substitute appropriate values of symbolic parameters and then apply Activate:
| In[12]:= |
| Out[12]= | 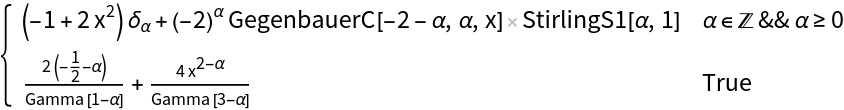 |
| In[13]:= |
| Out[13]= |
In cases where only partial evaluation is possible, results may be returned that contain unevaluated FractionalOrderD expressions:
| In[14]:= |
| Out[14]= |  |
Varying α from 0 to -1 smoothly interpolates between a function and its derivative:
| In[15]:= | ![f[x] := x^3 Sin[x];
Manipulate[
Plot[Evaluate@{f[x], D[f[x], x], ResourceFunction["FractionalOrderD"][f[x], {x, m}]}, {x, 0, 5}], {m, 0, -1}, SaveDefinitions -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/b8a/b8a39393-8652-47a7-95ad-cbc6bddd9685/090e785d0ca85bcd.png) |
| Out[15]= | 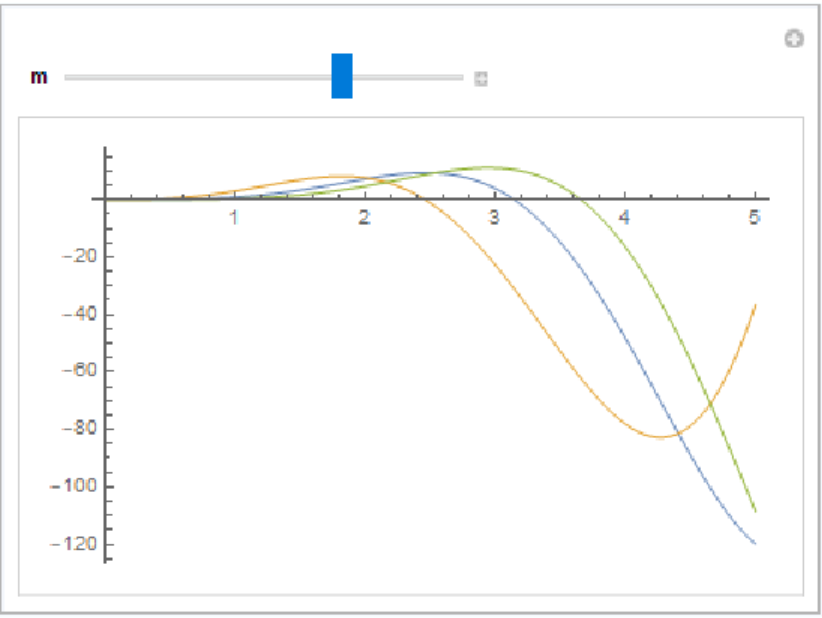 |
Create a table of fractional derivatives:
| In[16]:= |
| In[17]:= | ![Grid[Join[{{f[x], "FractionalOrderD"[f[x], {x, n}]}}, Transpose[{flist, ResourceFunction["FractionalOrderD"][flist, {x, n}]}]], Background -> {None, {{None, GrayLevel[.9]}}, {{1, 1} -> Hue[.6, .4, 1], {1, 2} -> Hue[.6, .4, 1]}}, BaseStyle -> {FontFamily -> Times, FontSize -> 12}, Dividers -> All,
FrameStyle -> Hue[.6, .4, .8], Spacings -> {2, 1}] // TraditionalForm](https://www.wolframcloud.com/obj/resourcesystem/images/b8a/b8a39393-8652-47a7-95ad-cbc6bddd9685/4d4d114e641c92f3.png) |
| Out[17]= |  |
This work is licensed under a Creative Commons Attribution 4.0 International License