Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 FractionalIteration

Source Notebook

Get the flow of an iterated function at a fixed point

Contributed by: Daniel Geisler

ResourceFunction["FractionalIteration"][f,t,order][x]

returns the power series of the flow associated with a fixed-point.

Details and Options

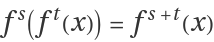
For the for the continuous or fractional iteration of a function f(x), dependent on continuous parameter s∈ℝ, fs(x) is called a flow if it satisfies the condition . Here, we work with finite iterations of a function so ResourceFunction["FractionalIteration"] can be considered as a discrete analog to a flow; where s is the integer number of iterations.
The following definitions are helpful for understanding ResourceFunction["FractionalIteration"]:
Super-attracting fixed point - dynamics described by Böttcher's equation. Typically does not produce a flow. f'(p)=0.
Hyperbolic fixed point - flow described by Schröder's equation for ft(x) where |f'(p)n|!=1 and fixed-point p is not a super-attractor.
Parabolic fixed point - flow described by Abel's equation for ft(x) where f'(p)=1.
Rationally neutral fixed point - rationally neutral flow when f'(p) is a root of unity, f'(p)n=1, n∈ℕ.
Irrationally neutral fixed point - irrationally neutral flow when |f'(p)|=1.
ResourceFunction["FractionalIteration"] computes flows of iterated functions including hyperbolic, parabolic, rationally neutral and irrationally neutral.
MethodAutomaticmethod to use
FixedPointpfixed point
ForceParabolicFalsesets first derivitive to 1
Being able to take the flow of maps allows not only tetration to be extended to the complex numbers, but all the higher hyperoperators. See the Neat Examples.

Examples

Basic Examples (4) 

The general hyperbolic flow power-series with a degree of 2:

In[1]:=
ResourceFunction["FractionalIteration"][f, t, 2][x]
Out[1]=

The general hyperbolic flow power-series with a degree of 3:

In[2]:=
ResourceFunction["FractionalIteration"][f, t, 3][x]
Out[2]=

The general parabolic flow solution with default degree of 4:

In[3]:=
ResourceFunction["FractionalIteration"][g, t, "ForceParabolic" -> True][x]
Out[3]=

The flow of the Sin function is an example of parabolic iteration:

In[4]:=
ResourceFunction["FractionalIteration"][Sin, t, 15, "FixedPoint" -> 0, "ForceParabolic" -> True][x]
Out[4]=

Properties and Relations (1) 

Show that the flow law is satisfied to order 4:

In[5]:=
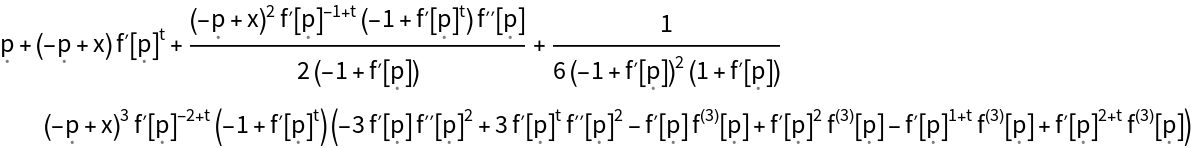
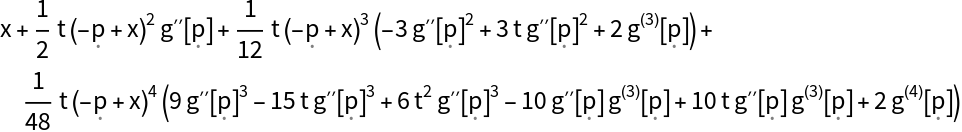
hyperbolicFlow = ResourceFunction["FractionalIteration"][f, t, 4, "FixedPoint" -> 0][ x]; error = (hyperbolicFlow /. t -> a /. x -> (hyperbolicFlow /. t -> b)) - (hyperbolicFlow /. t -> a + b); Series[error, {x, 0, 4}]
Out[7]=

Applications (2) 

Hyperbolic Tetration (2) 

Show a hyperbolic tetration of a function:

In[8]:=
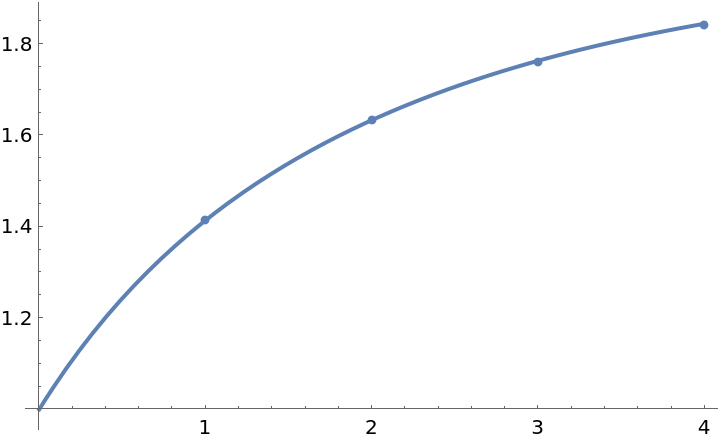
ht[z_] := N[Sqrt[2.]^z]; flowOrder = 4; tetration = ResourceFunction["FractionalIteration"][ht, x, flowOrder, "FixedPoint" -> 2][1]; Show[Plot[tetration, {x, 0, flowOrder}], ListPlot[NestList[ht, Sqrt[2.], flowOrder]]]
Out[9]=

Error between flow and iteration:

In[10]:=
N[Table[tetration, {x, -1, 6}] - NestList[ht, 0, 7], 10]
Out[10]=

Publisher

Daniel Geisler

Requirements

Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.0.0 – 07 July 2023

Source Metadata

  • Citation:
    J. Riordan, Combinatorial Identities, Wiley, 1968, L. Comtet, Advanced Combinatorics, Reidel, 1974, L. Carleson, T. Gamelin, Complex Dynamics, Springer-Verlag, 1993

Related Resources

Author Notes

FractionalIteration is meant to be the foundation of a ComplexAckermann function.

License Information