Basic Examples (2) 

Get a time series of closing prices and visualize it:

In[1]:=

Out[1]=

In[2]:=

Out[2]=

Compute the half difference of the time series and visualize it:

In[3]:=

Out[3]=

In[4]:=

Out[4]=

Scope (2) 

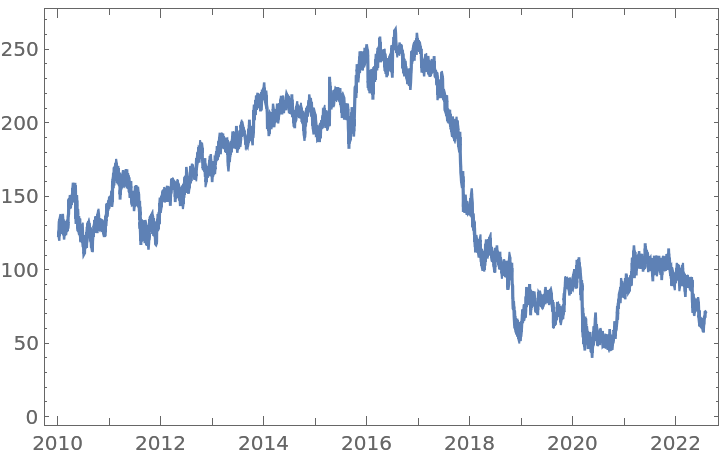
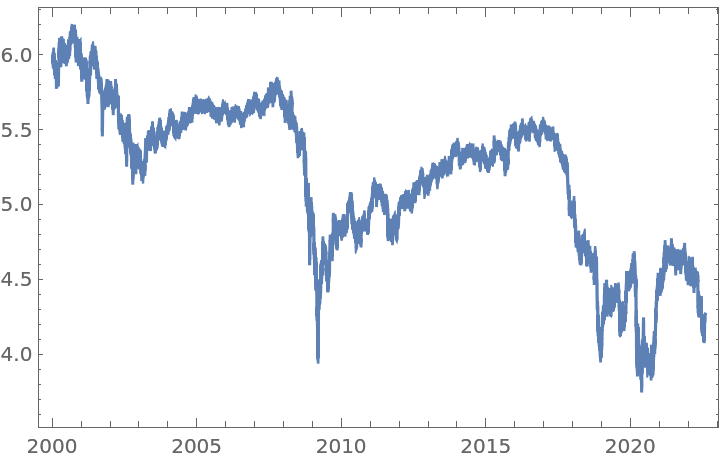
Get a time series of closing prices:

In[5]:=

Out[5]=

In[6]:=

Out[6]=

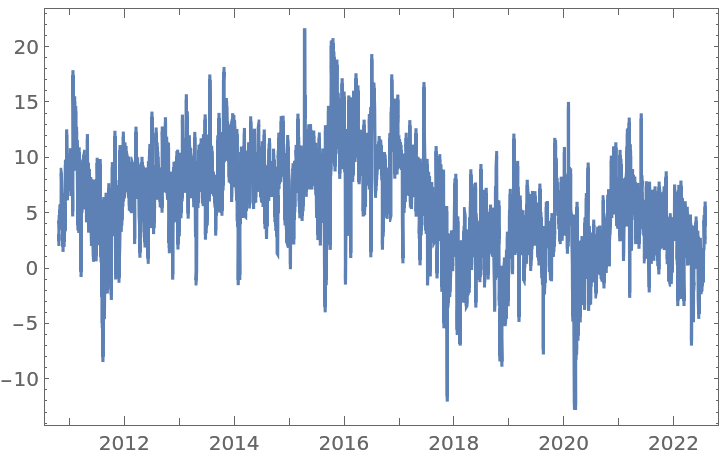
With order 1, FractionalDTimeSeries gives the usual first difference:

In[7]:=

Out[7]=

In[8]:=

Out[8]=

However, applying the half-difference twice on the original time series yields an equivalent first difference, but with fewer data points and on a slightly different scale:

In[9]:=

Out[9]=

In[10]:=

Out[10]=

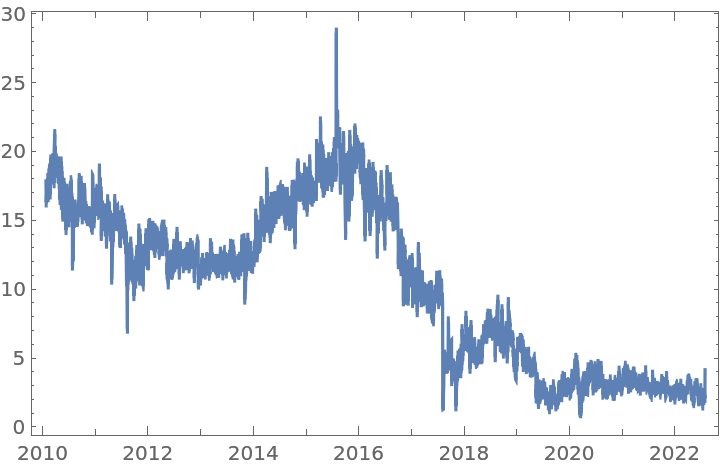
Get a time series of closing prices:

In[11]:=

Out[11]=

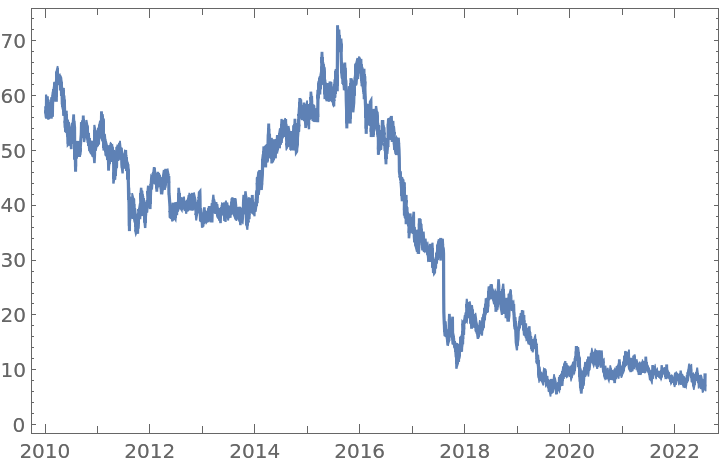
Apply a fractional difference of order 0.3531 to the original time series with the default tolerance:

In[12]:=

Out[12]=

In[13]:=

Out[13]=

For the same time series, a fractional difference of order 0.3531 and a larger tolerance will generate a time series with more data points:

In[14]:=

Out[14]=

In[15]:=

Out[15]=

In contrast, a fractional difference of the same order 0.3531, but with a smaller tolerance, will generate a time series with fewer data points:

In[16]:=

Out[16]=

In[17]:=

Out[17]=

Applications (3) 

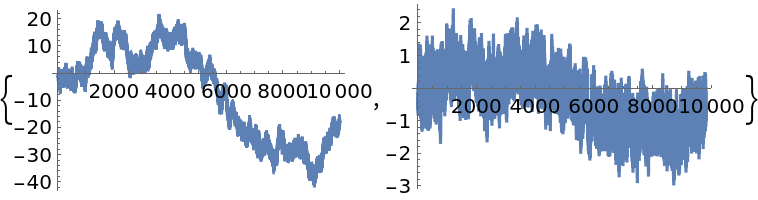
Simulate an ARIMAProcess with linear trend and apply a fractional difference of order 0.5:

In[18]:=

Out[19]=

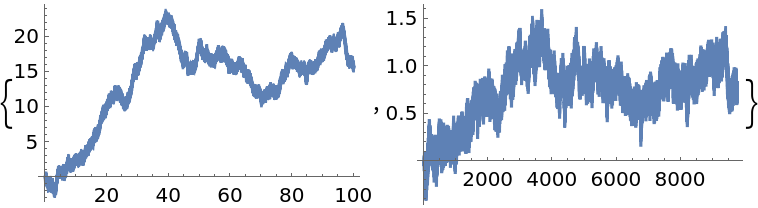
Simulate an FractionalBrownianMotionProcess with Hurst index 0.65 and apply a fractional difference of order 0.45 to it:

In[20]:=

Out[21]=

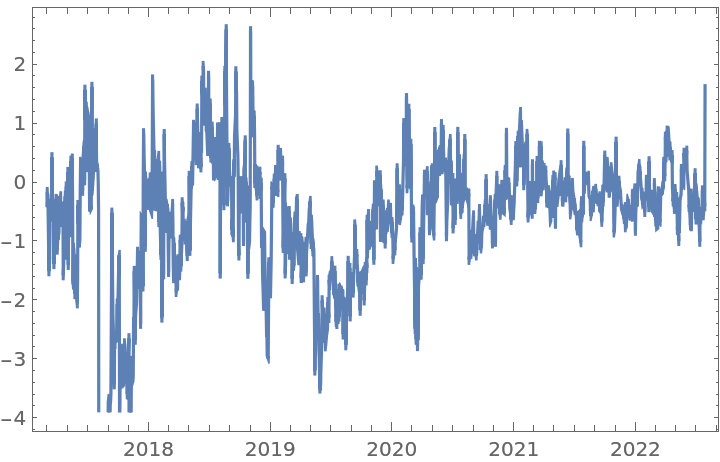
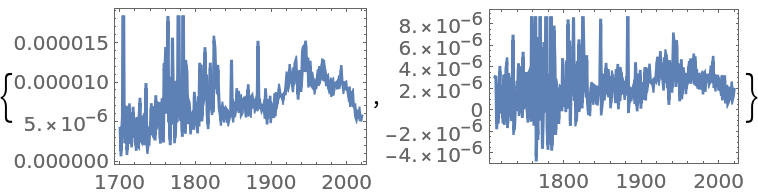
Get a time series of the frequencies of the word "Peru" in typical published text, and apply a fractional difference of order 0.35 and a tolerance of 0.01 to it:

In[22]:=

Out[23]=

Possible Issues (4) 

FractionalDTimeSeries requires the order to be a positive real number. Negative orders (integration) are currently not implemented:

In[24]:=

Out[24]=

FractionalDTimeSeries requires the tolerance to be positive:

In[25]:=

Out[25]=

If the tolerance is too small, no transformation will be performed:

In[26]:=

Out[26]=

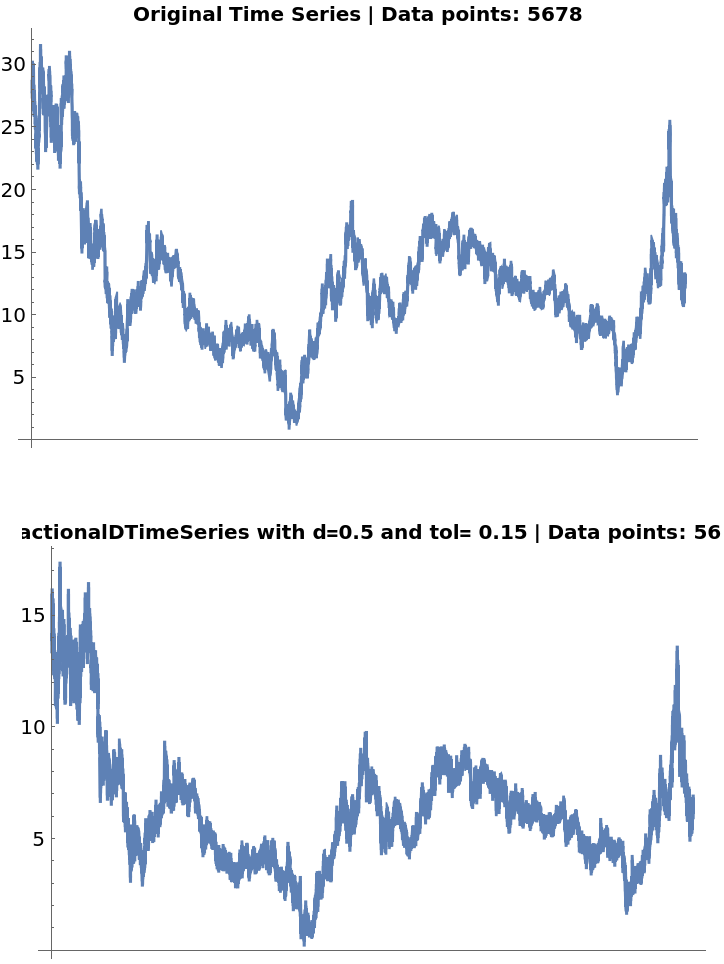
If the tolerance is set too high, the transformed time series will be essentially the same as the original one, but in a different scale:

In[27]:=

Out[28]=

In[29]:=

Out[29]=

Neat Examples (4) 

A logarithmically-transformed time series:

In[30]:=

Out[30]=

In[31]:=

Out[31]=

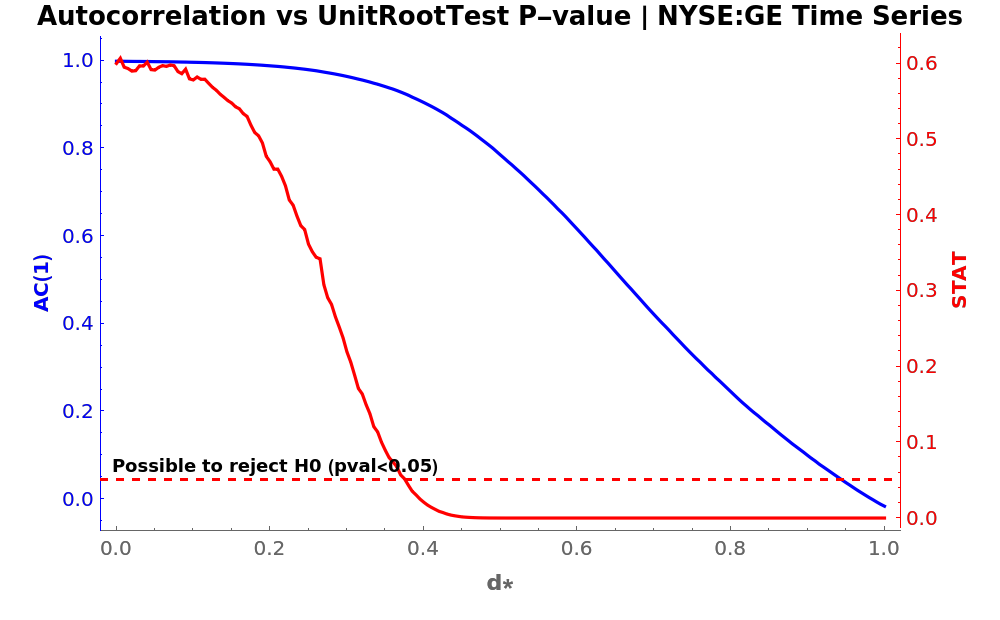
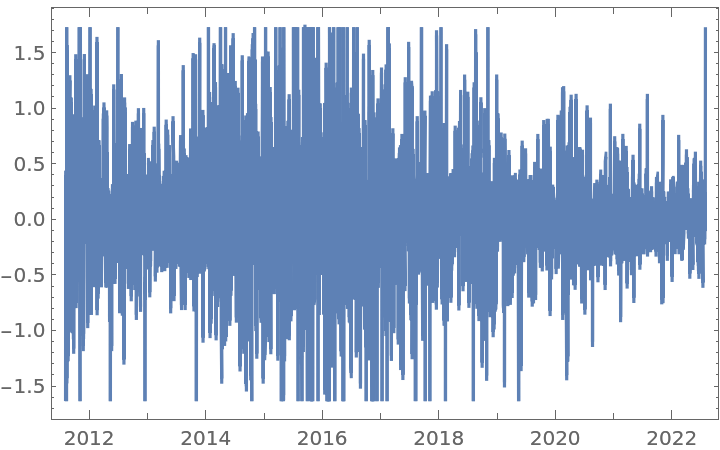
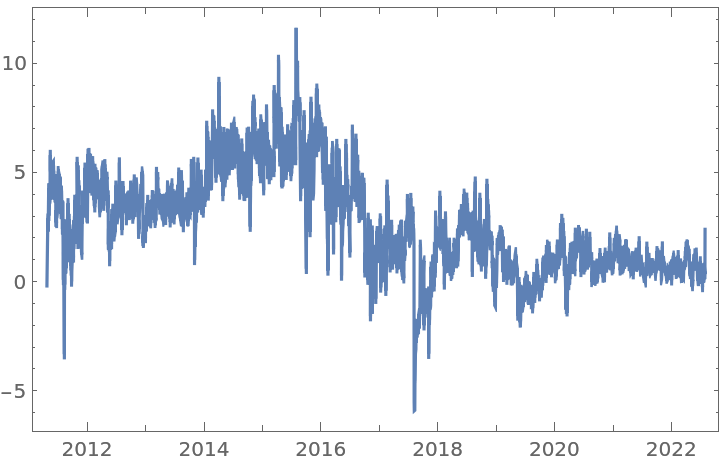
Find the relationship between the statistical value of a UnitRootTest and the CorrelationFunction of a transformed time series, by using several orders between 0 and 1:

In[32]:=

Apply a UnitRootTest (red axis) on each differentiated time series to see up from which level of d is possible to reject H₀. Also, compute its CorrelationFunction at lag 1 (blue axis) to compare:

In[33]:=

Plot the results:

In[34]:=

In[35]:=

Out[35]=