Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Calculate a fractional derivative
ResourceFunction["FractionalD"][f,{x,α}] gives the fractional derivative |
Half-derivative of x2:
| In[1]:= |
| Out[1]= |
Taking the half-derivative twice yields the usual first derivative:
| In[2]:= |
| Out[2]= |
If α is an integer, the result is the normal derivative:
| In[3]:= |
| Out[3]= |
Half-derivative of elementary functions:
| In[4]:= |
| Out[4]= | 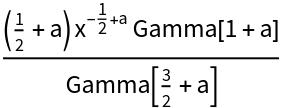 |
| In[5]:= |
| Out[5]= |
| In[6]:= |
| Out[6]= |
Half-derivative of trig functions:
| In[7]:= |
| Out[7]= |
| In[8]:= |
| Out[8]= |
Half-derivative of inverse trig functions:
| In[9]:= |
| Out[9]= |
| In[10]:= |
| Out[10]= | 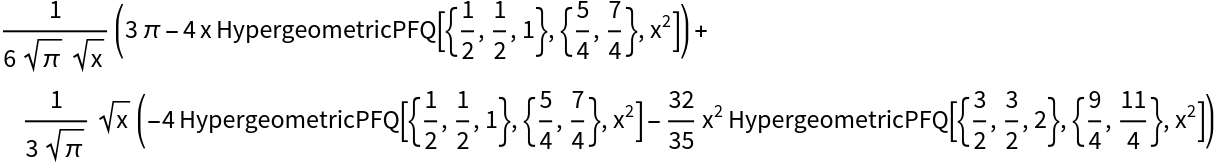 |
A more exotic fractional derivative:
| In[11]:= |
| Out[11]= | 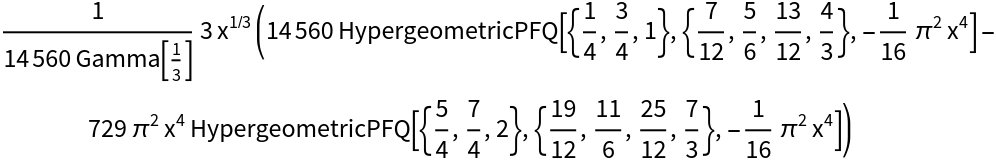 |
Choosing between Cauchy and Caputo may result in performance differences:
| In[12]:= |
| Out[12]= |
| In[13]:= |
| Out[13]= |
FractionalD uses integration under the hood. Sometimes the integral cannot be computed:
| In[14]:= |
| Out[14]= |
The fractional derivative smoothly interpolates between the function and its derivative:
| In[15]:= |
| Out[15]= | 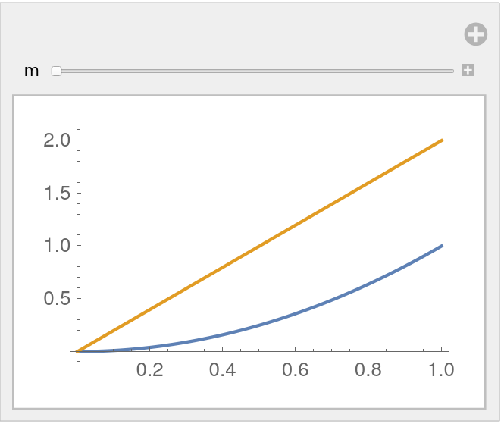 |
This work is licensed under a Creative Commons Attribution 4.0 International License