Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 FractionalBrownianMotion2D

Source Notebook

Generate a fractional Brownian surface

Contributed by: Roman E. Maeder

ResourceFunction["FractionalBrownianMotion2D"][n,h]

generate a natural surface of sizes n, with Hurst exponent h.

Details and Options

Fractional Brownian motion is a generalization of ordinary Brownian motion that has been used successfully to model a variety of natural phenomena, such as terrains, coastlines and clouds. It has the scaling property .
The Hurst exponent h describes the raggedness, with higher exponents leading to smoother surfaces. Ordinary Brownian motion has .
Methods for generating a fractional Brownian motion to simulate a natural surface are "RandomAddition" and "FourierSynthesis". The default method is "FourierSynthesis".
"RandomAddition" refines the list of points by interpolation and adding random offsets.
"FourierSynthesis" generates a random spectrum such that the resulting data has the correct scaling property.
For the "FourierSynthesis" method, n must be even.
The surfaces are colored by height using the "Topography" gradient mapping and level curves.

Examples

Basic Examples (2) 

Generate an ordinary Brownian surface:

In[1]:=
ResourceFunction["FractionalBrownianMotion2D"][70, .5]
Out[1]=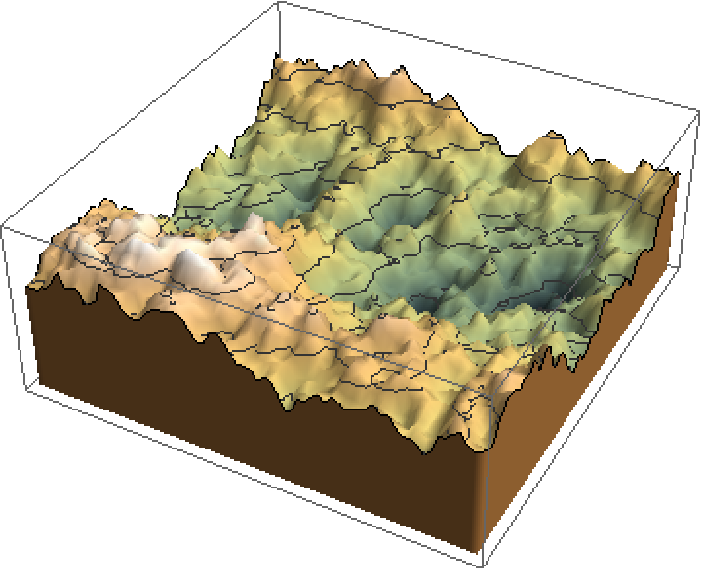

Generate a smoother Brownian surface:

In[2]:=
ResourceFunction["FractionalBrownianMotion2D"][70, .9]
Out[2]=

Options (1) 

Method (1) 

Modify Method:

In[3]:=
ResourceFunction["FractionalBrownianMotion2D"][20, .5, Method -> "RandomAddition"]
Out[3]=

Requirements

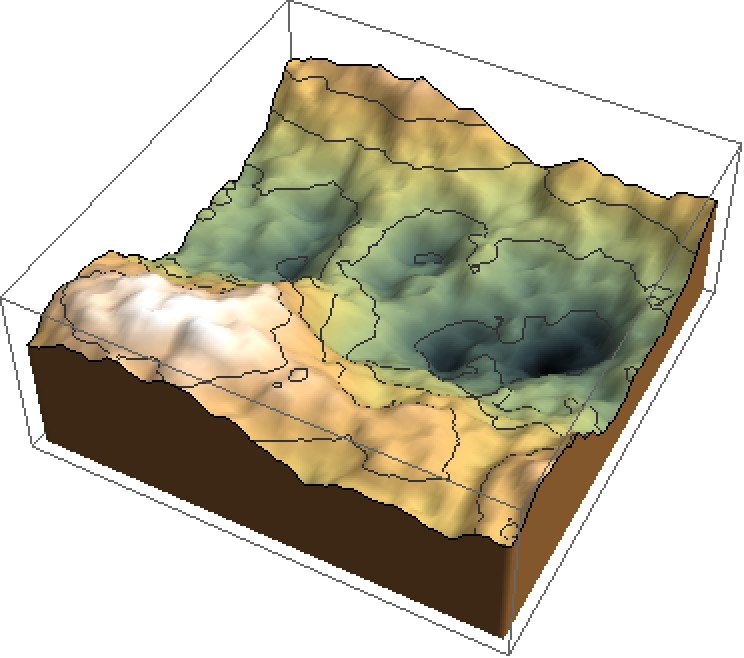Wolfram Language 11.3 (March 2018) or above

Version History

  • 1.0.0 – 17 April 2019

Source Metadata

  • Citation:
    • Maeder, R. E., The Mathematica Programmer II. New York: Academic Press, 1996.

License Information