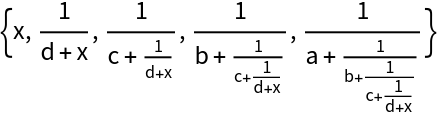Basic Examples (6)
Perform a right fold on a list:
Get cumulative sums of the elements of a list beginning from the end:
Cumulative powers:
Use the last element of the list as the starting value:
Use the operator form of FoldRightList on one argument:
Use the operator form of FoldRightList on two arguments:
Scope (1)
Perform a chain of cross products:
Generalizations and Extensions (4)
The head need not be List:
Use Unevaluated to fold prior to evaluation:
Hold and fold with Hold:
Fold to the left:
Or equivalently:
Applications (6)
Form alternating sums:
Form continued fractions:
Build up a nested polynomial (Horner form):
Build up a binary tree:
Form a sequence of function compositions:
Compare to using FoldList to form right compositions:
Form compositions of subvalues:
Properties and Relations (7)
FoldRightList makes a list of length n+1:
Folding with an empty list does not apply the function at all:
The resource function FoldRight gives the last element of FoldRightList:
Functions that ignore their first argument give the same result as NestList:
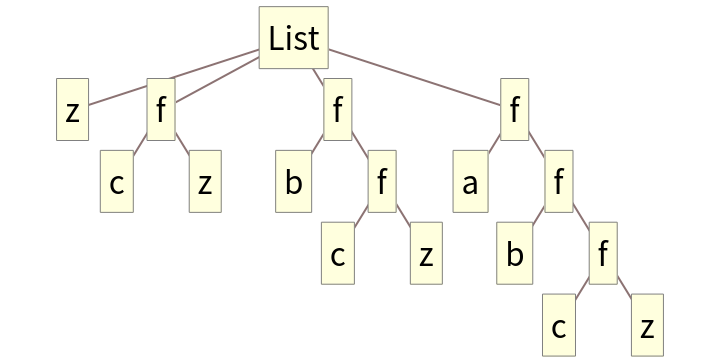
Compare FoldRightList to FoldList structurally:
In both cases, each item in the list is a subtree of the next:
The order of arguments passed to f are reversed compared to FoldList:
FoldRightList takes elements starting on the right of the given list:
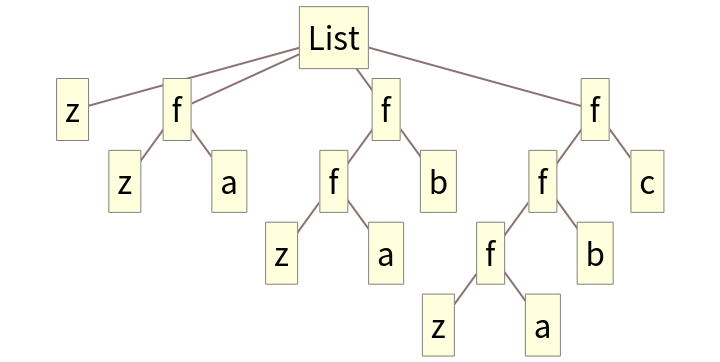
Compare to FoldList:
Possible Issues (2)
FoldRightList[f,{}] evaluates to an empty list, without a last element:
Therefore, FoldRight[f,{}] is undefined:
Elements are taken in reverse order:
Compare to a typical recursive definition of foldr:
This implementation allows FoldRightList to be tail recursive, which is far more efficient with respect to stack size:
Without tail recursion, the stack size would grow with respect to the size of the list:
Neat Examples (1)
Compute a four-fold bird fold for fun: