Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Find the equation for a hyperbola given two foci and a point
ResourceFunction["FociPointHyperbola"][{f1,f2,p},{x,y}] returns the hyperbola A x2+B x y+C y2+D x+E y+F in the variables x and y, given the foci f1,f2 and a point p through which the hyperbola passes. | |
ResourceFunction["FociPointHyperbola"][{f1,f2,p},t] returns a parametric equation in the variable t. |
Find the Cartesian equation of a hyperbola with foci (2,2) and (3,5) that goes through point (1,3):
| In[1]:= |
| Out[2]= |
Show the hyperbola:
| In[3]:= |
| Out[3]= | 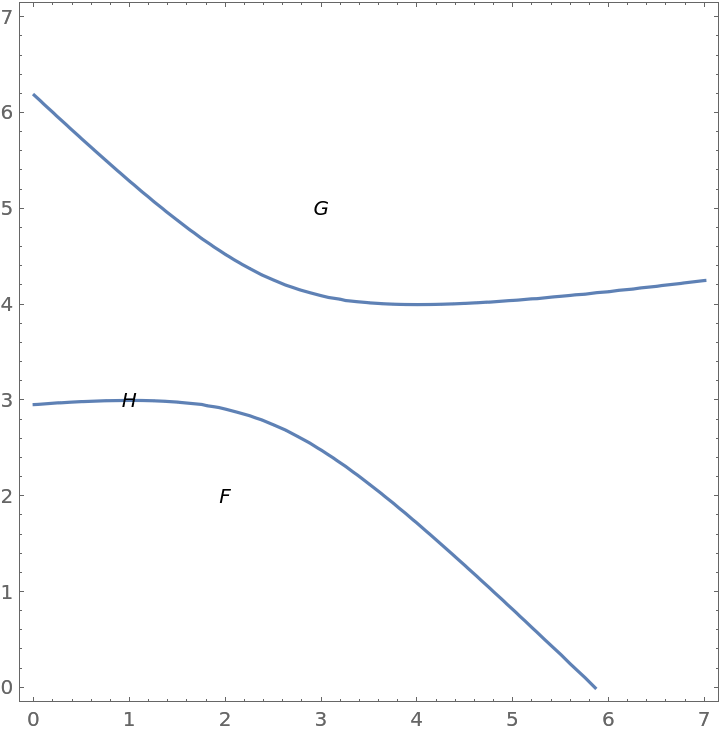 |
Find the three hyperbolas generated by the three points:
| In[4]:= |
| Out[4]= |
The three hyperbolas happen to intersect at the inner and outer Soddy centers for triangle ΔFGH:
| In[5]:= |
| Out[5]= | 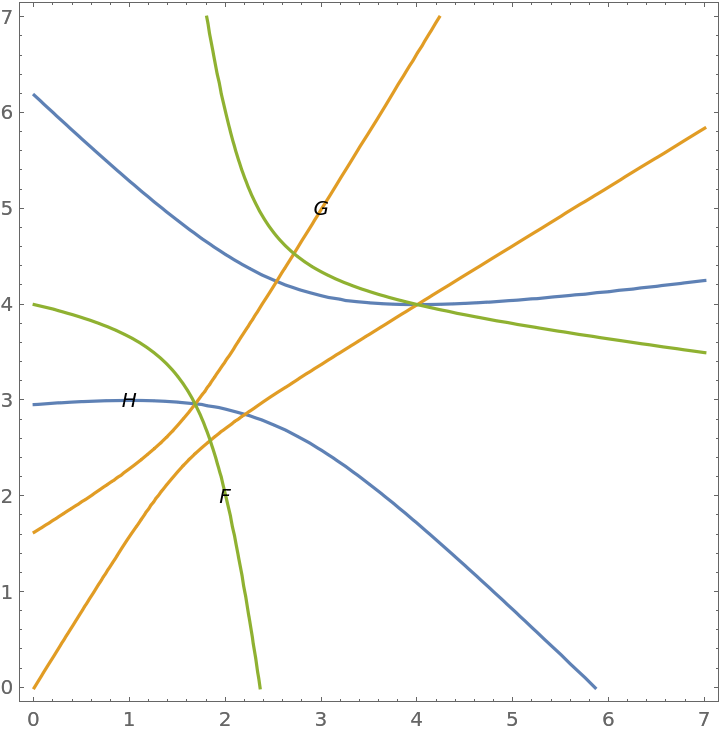 |
Generate the parametric equations of a hyperbola with foci (2,2) and (3,5) that goes through point (1,3):
| In[6]:= |
| Out[7]= |
Show the hyperbola:
| In[8]:= |
| Out[8]= | 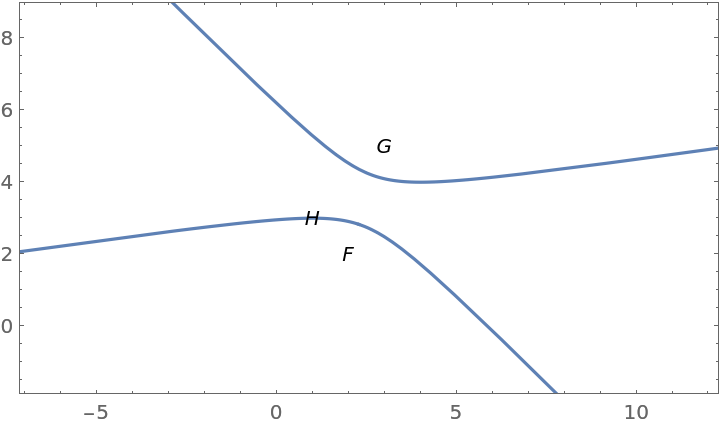 |
Use a different set of variables:
| In[9]:= |
| Out[9]= |
Use formal variables:
| In[10]:= |
| Out[10]= |
If no variables are given, formal variables are used by default:
| In[11]:= |
| Out[11]= |
Use FociPointHyperbola to generate the implicit Cartesian equation of a hyperbola:
| In[12]:= | ![{F, G, H} = {{8, 0}, {0, 6}, {18/5, 33/10}};
ResourceFunction["FociPointHyperbola"][{F, G, H}, {x, y}]](https://www.wolframcloud.com/obj/resourcesystem/images/af2/af25de5d-91f5-46b5-9ad2-ba5607ad3b6f/4fb9043611b74f0f.png) |
| Out[13]= |
Use GroebnerBasis to get an equivalent result:
| In[14]:= | ![First[GroebnerBasis[
Sqrt[# . # &[{x, y} - F]] - Sqrt[# . # &[{x, y} - G]] == Sqrt[# . # &[H - F]] - Sqrt[# . # &[H - G]], {x, y}]]](https://www.wolframcloud.com/obj/resourcesystem/images/af2/af25de5d-91f5-46b5-9ad2-ba5607ad3b6f/2c6ee95fcc6347c0.png) |
| Out[14]= |
Generate an equivalent parametric equation:
| In[15]:= |
| Out[15]= |
Use GroebnerBasis to derive the implicit Cartesian equation from the parametric equation:
| In[16]:= |
| Out[16]= |
Use the resource function HyperbolaProperties to generate properties of the hyperbola:
| In[17]:= | ![ResourceFunction["HyperbolaProperties"][
ResourceFunction[
"FociPointHyperbola"][{{0, 0}, {5, 7}, {2, 1}}, {x, y}] == 0, {x, y}]](https://www.wolframcloud.com/obj/resourcesystem/images/af2/af25de5d-91f5-46b5-9ad2-ba5607ad3b6f/17383d27ddc20da9.png) |
| Out[17]= |  |
Get a hyperbola equation:
| In[18]:= |
| Out[18]= |
Show positions for coefficients in A x2+B x y+C y2+D x+E y+F=0:
| In[19]:= |
| Out[19]= |
Get the coefficients:
| In[20]:= |
| Out[20]= |
See the coefficients in the standard order:
| In[21]:= |
| Out[21]= |
Three arbitrary circles and some middle circles:
| In[22]:= | ![circs = {Circle[{0, 0}, 1], Circle[{8, 0}, 3], Circle[{0, 6}, 2]};
Graphics[{circs, Green, Circle[{3, 0}, 2], Circle[{0, 5/2}, 3/2], Circle[{18/5, 33/10}, 5/2]}]](https://www.wolframcloud.com/obj/resourcesystem/images/af2/af25de5d-91f5-46b5-9ad2-ba5607ad3b6f/6845f800a4c1d527.png) |
| Out[23]= | 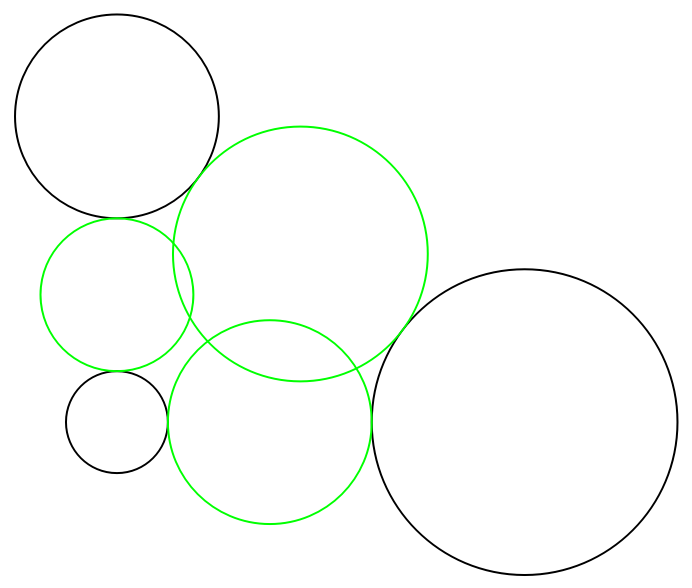 |
Find the three hyperbolas using two circle centers and a midcircle center:
| In[24]:= | ![ab = ResourceFunction[
"FociPointHyperbola"][{{0, 0}, {8, 0}, {3, 0}}, {x, y}];
ac = ResourceFunction[
"FociPointHyperbola"][{{0, 0}, {0, 6}, {0, 5/2}}, {x, y}];
bc = ResourceFunction[
"FociPointHyperbola"][{{8, 0}, {0, 6}, {18/5, 33/10}}, {x, y}];](https://www.wolframcloud.com/obj/resourcesystem/images/af2/af25de5d-91f5-46b5-9ad2-ba5607ad3b6f/4955c5de0677fe84.png) |
Find real-valued intersection points of the three hyperbolas:
| In[25]:= |
| Out[25]= |
Find a few distances:
| In[26]:= |
Show two circles tangent to the given circles:
| In[27]:= |
| Out[27]= |  |
This work is licensed under a Creative Commons Attribution 4.0 International License