Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Produce random causal graphs by sprinkling points into flat (Minkowski) spacetime
ResourceFunction["FlatSpacetimeSprinkling"][dim,n] produces a random sprinkling of n points into a flat (Minkowski) spacetime of dimension (dim-1)+1. | |
ResourceFunction["FlatSpacetimeSprinkling"][dim,n,"prop"] gives the property "prop" for the specified flat (Minkowski) spacetime sprinkling. |
| "CausalGraphFull" | full causal partial order graph (before transitive reduction) |
| "CausalGraph" | transitively reduced causal partial order graph |
| "Points" | plot of the sprinkled points only (without causal edges) |
| "PointsList" | list of the spacetime coordinates of all sprinkled points |
| "PointsCount" | number of sprinkled points |
| "Dimensions" | number of dimensions in the continuum spacetime approximation |
| "TotalEdgeCount" | total number of causal edges (before transitive reduction) |
| "ReducedEdgeCount" | number of transitively reduced causal edges |
| "PureCausalGraphFull" | full causal partial order graph (before transitive reduction) with vertex coordinate information removed |
| "PureCausalGraph" | transitively reduced causal partial order graph with vertex coordinate information removed |
| "Properties" | list of properties |
Produce a random sprinkling of 20 points into a 1+1-dimensional flat (Minkowski) spacetime:
| In[1]:= |
| Out[1]= |  |
Show the causal graph:
| In[2]:= |
| Out[2]= | 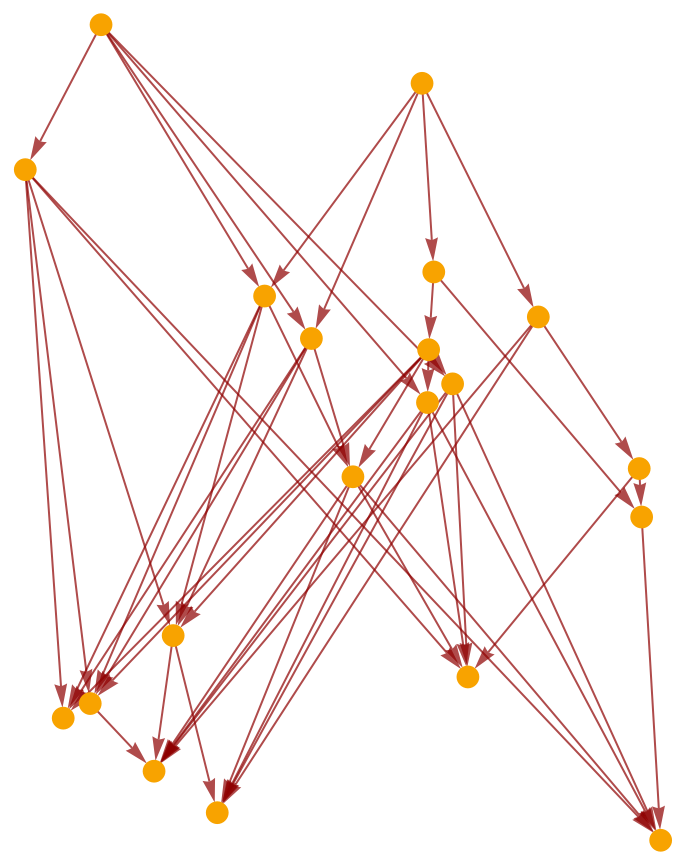 |
Show the full causal graph (without transitive reduction):
| In[3]:= |
| Out[3]= | 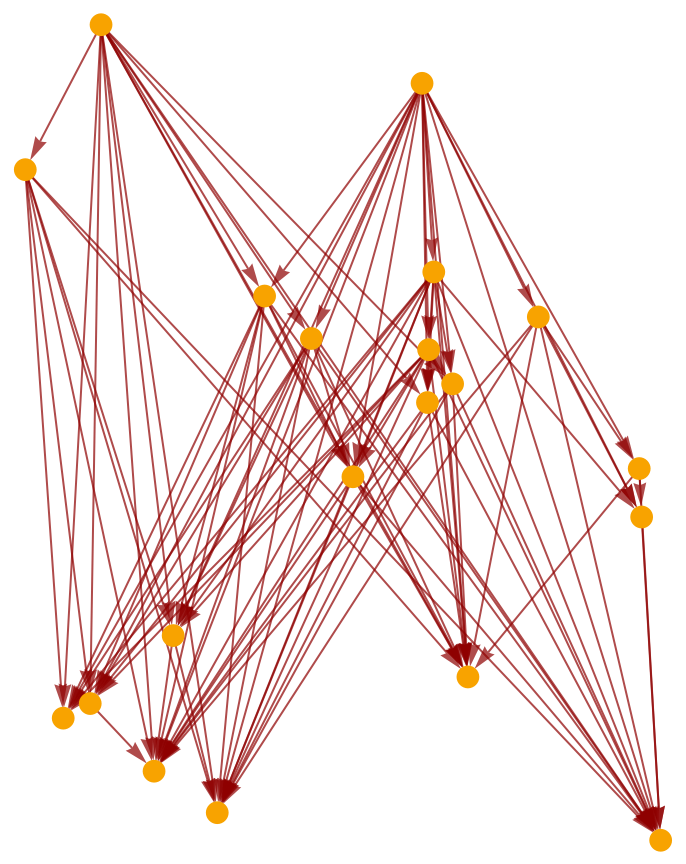 |
Produce a random sprinkling of 100 points into a 2+1-dimensional flat (Minkowski) spacetime:
| In[4]:= |
| Out[4]= |  |
Show the causal graph:
| In[5]:= |
| Out[5]= | 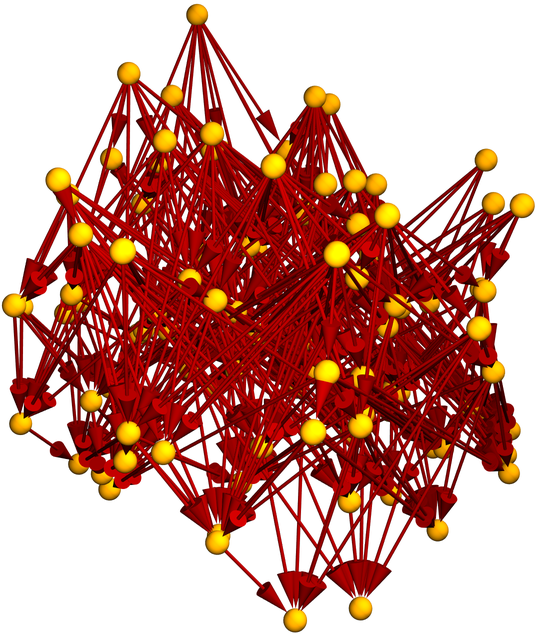 |
Show the pure causal graph (with vertex coordinate information removed):
| In[6]:= |
| Out[6]= |  |
Show the pure causal graph with a layered graph embedding:
| In[7]:= |
| Out[7]= |  |
Sprinklings can be produced in arbitrary (integer) numbers of dimensions:
| In[8]:= |
| Out[8]= |
| In[9]:= |
| Out[9]= | 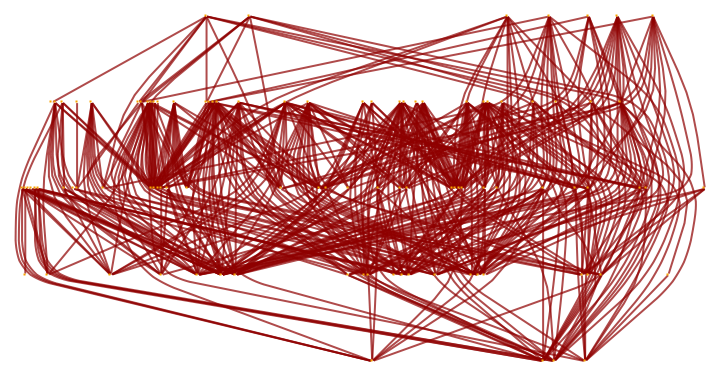 |
| In[10]:= |
| Out[10]= |
| In[11]:= |
| Out[11]= |  |
Properties can be requested directly from FlatSpacetimeSprinkling:
| In[12]:= |
| Out[12]= | 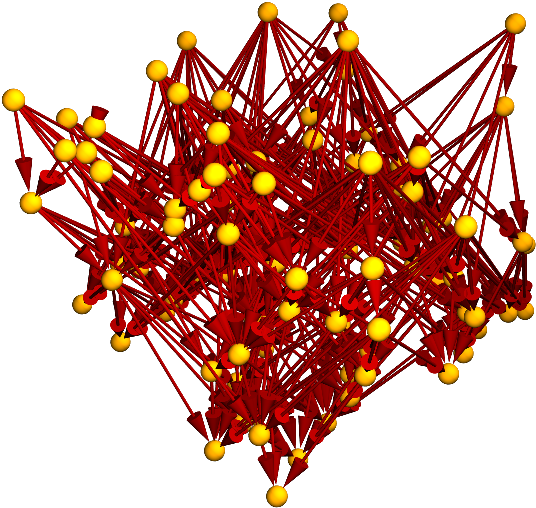 |
Produce a random sprinkling of 100 points into a 1+1-dimensional flat (Minkowski) spacetime:
| In[13]:= |
| Out[13]= |
Show the complete list of properties:
| In[14]:= |
| Out[14]= |
Show the full causal graph:
| In[15]:= |
| Out[15]= | 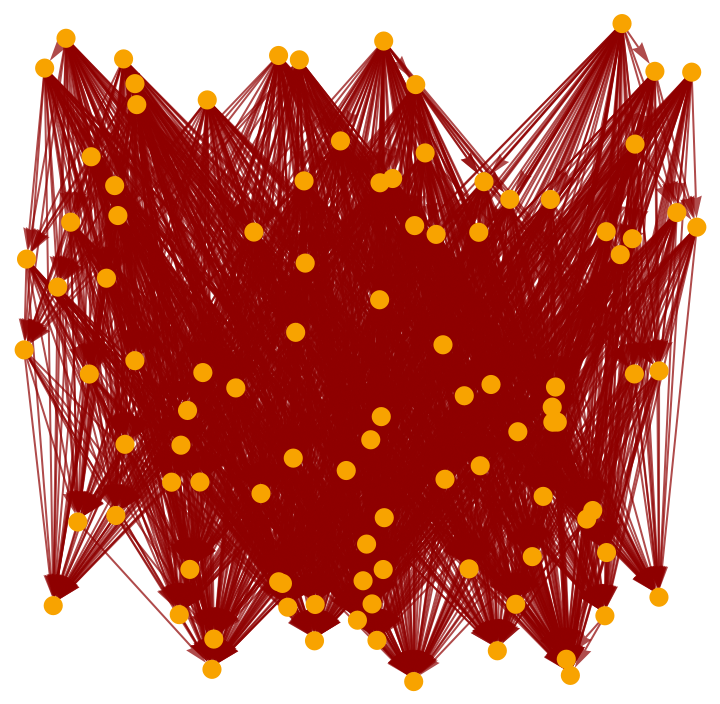 |
Show the transitively reduced causal graph:
| In[16]:= |
| Out[16]= | 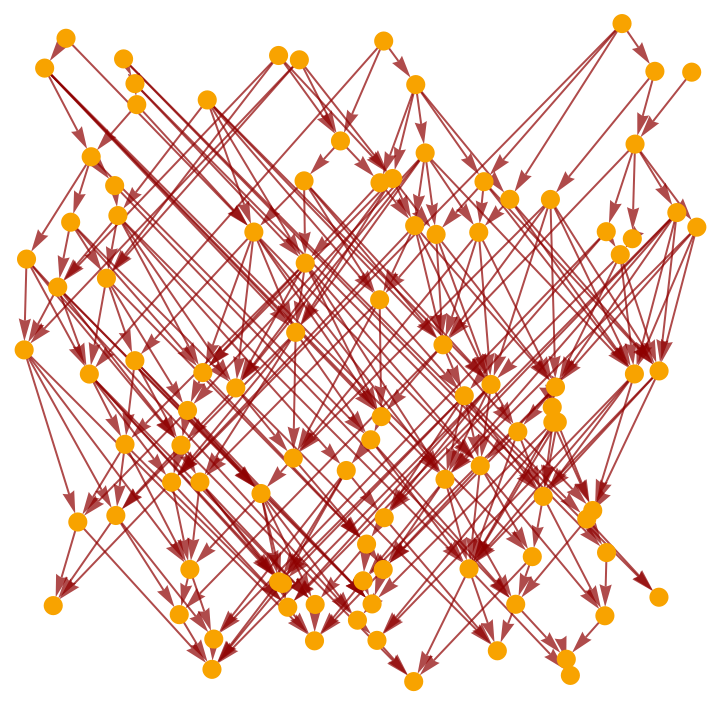 |
Plot the positions of the sprinkled points only (without causal edges):
| In[17]:= |
| Out[17]= |  |
Show a complete list of spacetime coordinates for the sprinkled points (the last coordinate is always the time coordinate):
| In[18]:= |
| Out[18]= |  |
Show the number of sprinkled points:
| In[19]:= |
| Out[19]= |
Show the number of dimensions in the background spacetime:
| In[20]:= |
| Out[20]= |
Show the total number of causal edges:
| In[21]:= |
| Out[21]= |
Show the number of causal edges after transitive reduction:
| In[22]:= |
| Out[22]= |
Show the pure full causal graph (with vertex coordinate information removed):
| In[23]:= |
| Out[23]= | 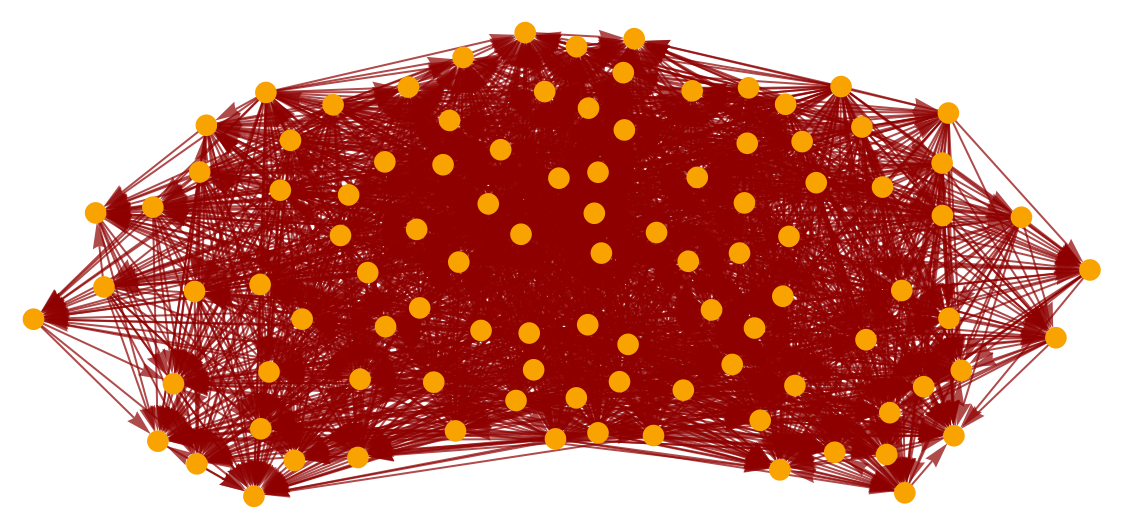 |
Show the pure transitively reduced causal graph (with vertex coordinate information removed):
| In[24]:= |
| Out[24]= |  |
This work is licensed under a Creative Commons Attribution 4.0 International License