Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Plot fitted models together with their raw data
ResourceFunction["FittedModelPlot"][FittedModel[…]] plots the raw data and the fit described by the FittedModel[…] expression. | |
ResourceFunction["FittedModelPlot"][FittedModel[…],lims] plots the fit over the range given by lims. | |
ResourceFunction["FittedModelPlot"][{FittedModel[…],FittedModel[…]},…] plots several fit results. | |
ResourceFunction["FittedModelPlot"][{…,w[FittedModel[…],…],…},…] plots the FittedModel[…] with features defined by the symbolic wrapper w. | |
ResourceFunction["FittedModelPlot"][data,funcs,x] computes the fit from LinearModelFit[data,funcs,x]. | |
ResourceFunction["FittedModelPlot"][data,form,params,x] computes the fit from NonlinearModelFit[data,form,params,x]. | |
ResourceFunction["FittedModelPlot"][{data1,data2,…},…,x] computes the fits for several datai. | |
ResourceFunction["FittedModelPlot"][data,…,{x,xmin,xmax}] plots the fit from xmin to xmax. | |
ResourceFunction["FittedModelPlot"][{…,w[datai,…],…},…] plots datai with features defined by the symbolic wrapper w. |
| "ErrorBands" | False | whether to plot the error bands of the fits |
| LegendFunction | Automatic | how to generate the plot legend |
Fit data using LinearModelFit and plot the result:
| In[1]:= | ![data = {{0, 1}, {1, 0}, {3, 2}, {5, 4}};
lm = LinearModelFit[data, x, x];
ResourceFunction["FittedModelPlot"][lm]](https://www.wolframcloud.com/obj/resourcesystem/images/647/6474b83d-a789-419f-88d3-79e5c2edc399/00ff030f9750d35a.png) |
| Out[3]= | 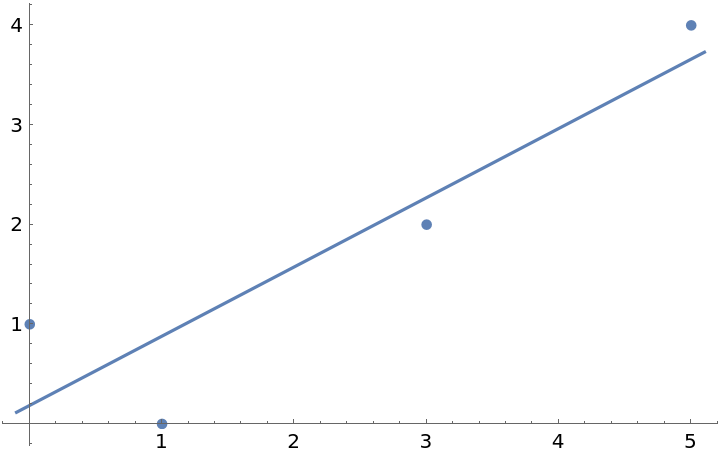 |
Plot two fits:
| In[4]:= | ![data = {{0, 1}, {1, 0}, {3, 2}, {5, 4}};
data2 = {{0, 3}, {1, 4}, {3, 4}, {5, 6}};
lm = LinearModelFit[data, x, x];
lm2 = LinearModelFit[data2, x, x];
ResourceFunction["FittedModelPlot"][{lm, lm2}]](https://www.wolframcloud.com/obj/resourcesystem/images/647/6474b83d-a789-419f-88d3-79e5c2edc399/3eec53bb8cc53e28.png) |
| Out[8]= | 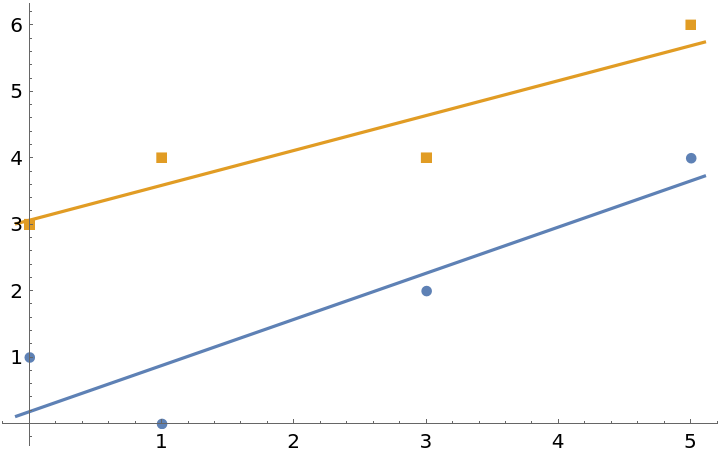 |
Style the plot and add a legend:
| In[9]:= | ![data = {{0, 5}, {1, 2}, {3, 2}, {5, 1}};
data2 = {{0, 3}, {1, 4}, {3, 4}, {5, 6}};
lm = LinearModelFit[data, x, x];
lm2 = LinearModelFit[data2, x, x];
ResourceFunction[
"FittedModelPlot"][<|"Data 1" -> lm, "Data 2" -> lm2|>,
Frame -> True, PlotStyle -> Directive[Dashed, Thick], PlotTheme -> "VibrantColor"]](https://www.wolframcloud.com/obj/resourcesystem/images/647/6474b83d-a789-419f-88d3-79e5c2edc399/5a18663709db14f7.png) |
| Out[13]= | 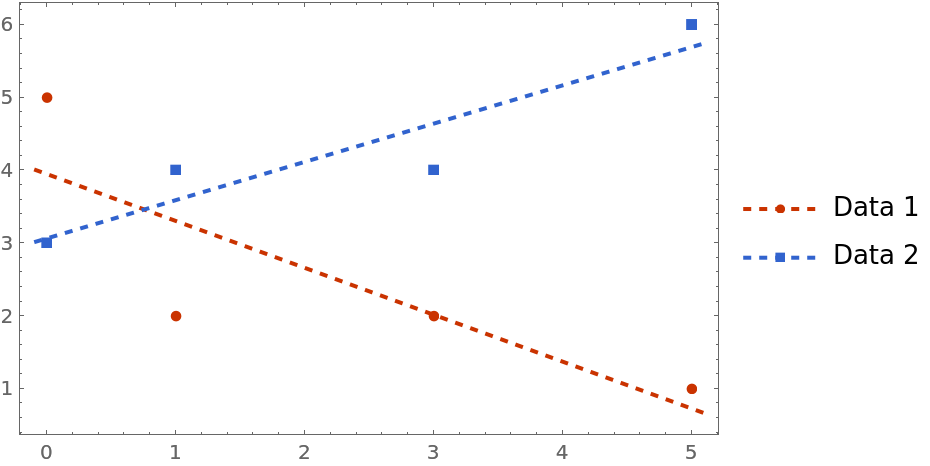 |
Supply the data to FittedModelPlot directly:
| In[14]:= | ![data = {{0, 5}, {1, 2}, {3, 2}, {5, 1}};
data2 = {{0, 3}, {1, 4}, {3, 4}, {5, 6}};
ResourceFunction["FittedModelPlot"][
<|"Data 1" -> data, "Data 2" -> data2|>, x, x,
Frame -> True, PlotStyle -> Directive[Dashed, Thick], PlotTheme -> "VibrantColor", "ErrorBands" -> True
]](https://www.wolframcloud.com/obj/resourcesystem/images/647/6474b83d-a789-419f-88d3-79e5c2edc399/1639f0af1fe90778.png) |
| Out[16]= | 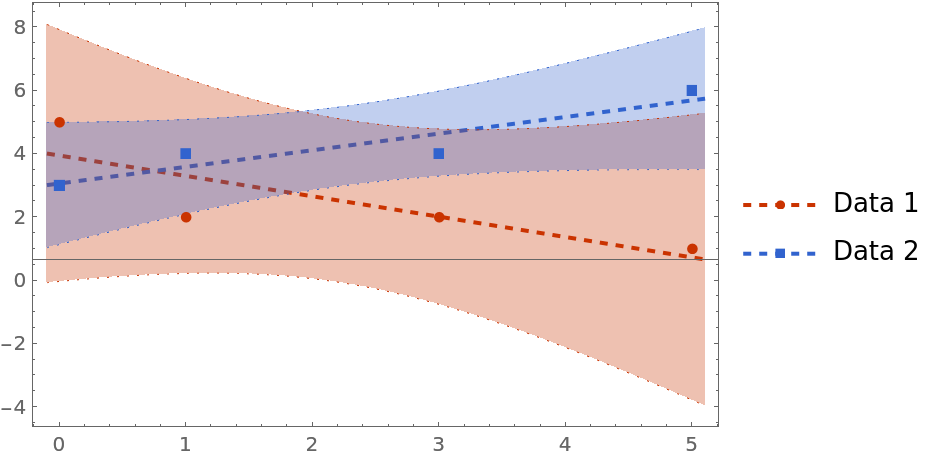 |
Specify labels and callouts via wrappers, and specify that the callout should be attached to the fit line:
| In[17]:= | ![data = {{0, 1}, {1, 0}, {3, 2}, {5, 4}};
data2 = {{0, 3}, {1, 4}, {3, 4}, {5, 6}};
ResourceFunction["FittedModelPlot"][
<|"Data 1" -> Callout[data, "Some callout", {Fit, 2}], "Data 2" -> Labeled[data2, "Some label", {Scaled@1, Before}]|>,
x,
x,
Frame -> True
]](https://www.wolframcloud.com/obj/resourcesystem/images/647/6474b83d-a789-419f-88d3-79e5c2edc399/31786a36f7eb1680.png) |
| Out[19]= | 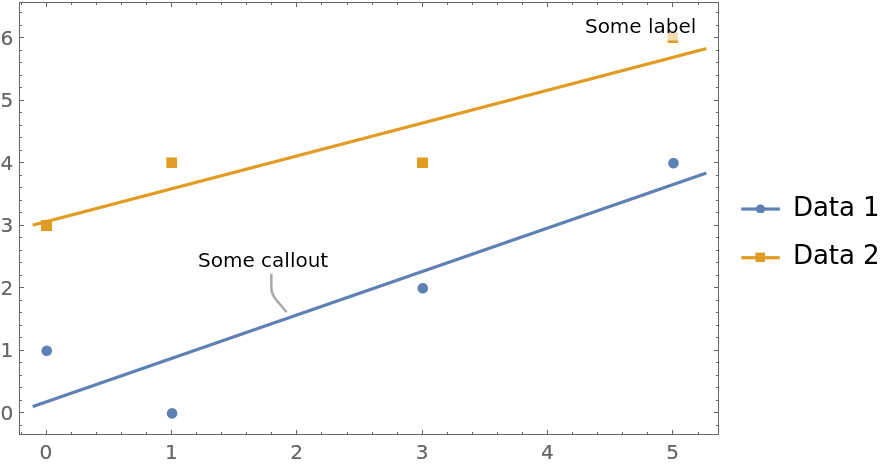 |
Plot the fit over a wider range:
| In[20]:= | ![data = {{0, 1}, {1, 0}, {3, 2}, {5, 4}};
lm = LinearModelFit[data, x, x];
ResourceFunction["FittedModelPlot"][lm, {-2, 8}, Frame -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/647/6474b83d-a789-419f-88d3-79e5c2edc399/3d68c042746e36de.png) |
| Out[22]= | 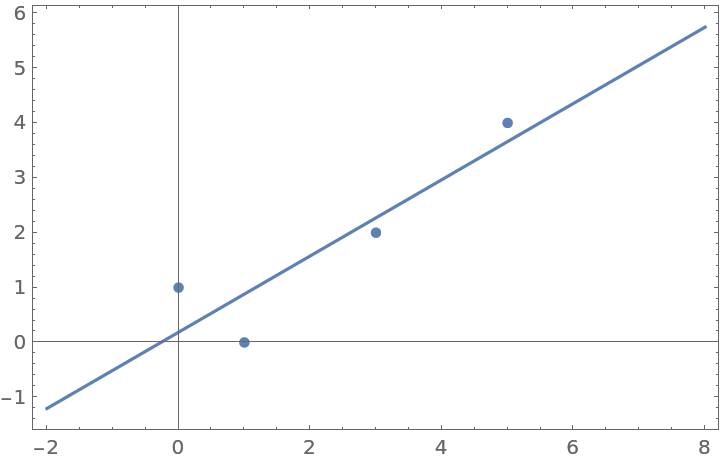 |
With the default setting "ErrorBands"→False, no error bands are plotted:
| In[23]:= | ![data = {{0, 1}, {1, 0}, {3, 2}, {5, 4}};
lm = LinearModelFit[data, x, x];
ResourceFunction["FittedModelPlot"][lm]](https://www.wolframcloud.com/obj/resourcesystem/images/647/6474b83d-a789-419f-88d3-79e5c2edc399/6828651417d07481.png) |
| Out[25]= | 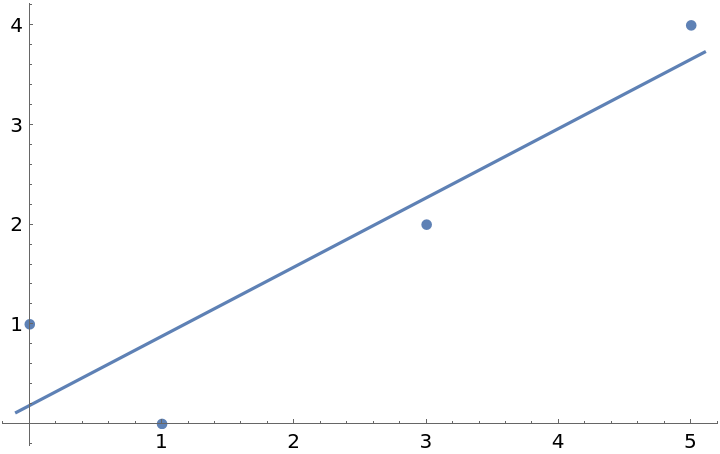 |
Add error bands to the plot:
| In[26]:= | ![data = {{0, 1}, {1, 0}, {3, 2}, {5, 4}};
lm = LinearModelFit[data, x, x];
ResourceFunction["FittedModelPlot"][lm, "ErrorBands" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/647/6474b83d-a789-419f-88d3-79e5c2edc399/56beef076d2ca6c0.png) |
| Out[28]= |  |
The setting for ConfidenceLevel affects the error bands:
| In[29]:= | ![data = {{0, 1}, {1, 0}, {3, 2}, {5, 4}};
lm = LinearModelFit[data, x, x];
ResourceFunction["FittedModelPlot"][lm, ConfidenceLevel -> 0.7, "ErrorBands" -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/647/6474b83d-a789-419f-88d3-79e5c2edc399/074df32ff03c3cdd.png) |
| Out[31]= | 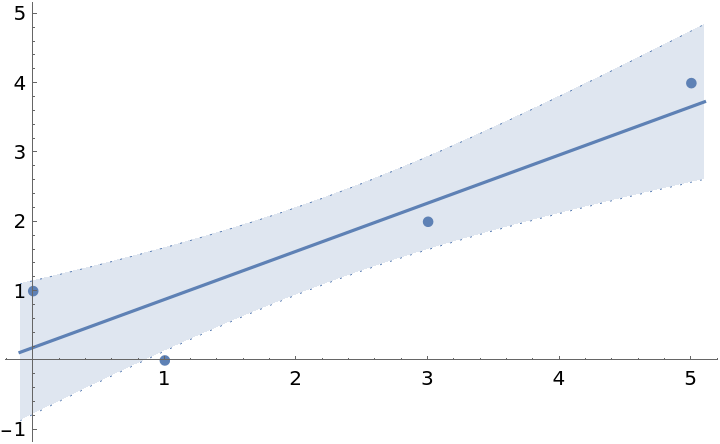 |
With the default setting LegendFunction→Automatic, the legend is effectively generated from the PlotLegends setting:
| In[32]:= | ![data = {
{{0, 2}, {1, 1}, {3, 3}, {5, 7}, {6, 5}, {7, 8}},
{{0, 1}, {1, 0}, {3, 2}, {5, 4}, {6, 4}, {7, 5}}
};
ResourceFunction["FittedModelPlot"][data, Log[a + b x^2], {a, b}, x, PlotLegends -> {"A", "B"}]](https://www.wolframcloud.com/obj/resourcesystem/images/647/6474b83d-a789-419f-88d3-79e5c2edc399/4eb412518d23c346.png) |
| Out[33]= | 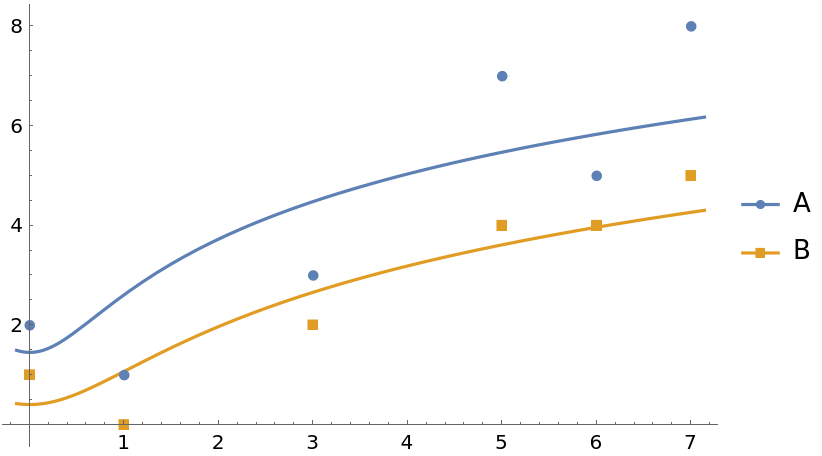 |
Give a function to compute the legend from the FittedModel[…] expressions:
| In[34]:= | ![data = {
{{0, 2}, {1, 1}, {3, 3}, {5, 7}, {6, 5}, {7, 8}},
{{0, 1}, {1, 0}, {3, 2}, {5, 4}, {6, 4}, {7, 5}}
};
ResourceFunction["FittedModelPlot"][data, Log[a + b x^2], {a, b}, x, LegendFunction -> Map[#["BestFit"] &]]](https://www.wolframcloud.com/obj/resourcesystem/images/647/6474b83d-a789-419f-88d3-79e5c2edc399/0a8162c103e54df0.png) |
| Out[35]= | 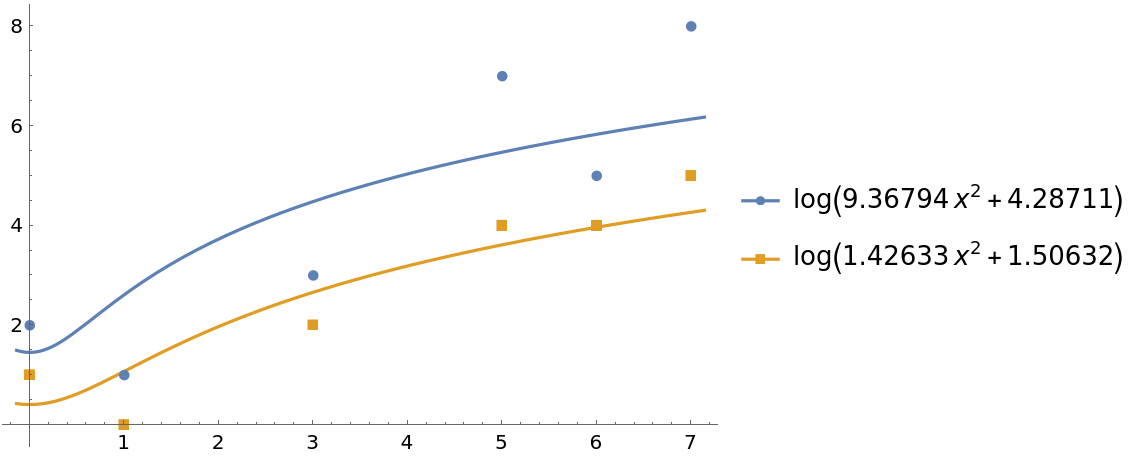 |
FittedModelPlot can be recreated using a combination of ListPlot and Plot:
| In[36]:= | ![data = {{0, 1}, {1, 0}, {3, 2}, {5, 4}, {6, 4}, {7, 5}};
nlm = NonlinearModelFit[data, Log[a + b x^2], {a, b}, x];
Show[ListPlot[data], Plot[nlm[x], {x, 0, 7}], Frame -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/647/6474b83d-a789-419f-88d3-79e5c2edc399/246c45e9ce330c2c.png) |
| Out[38]= | 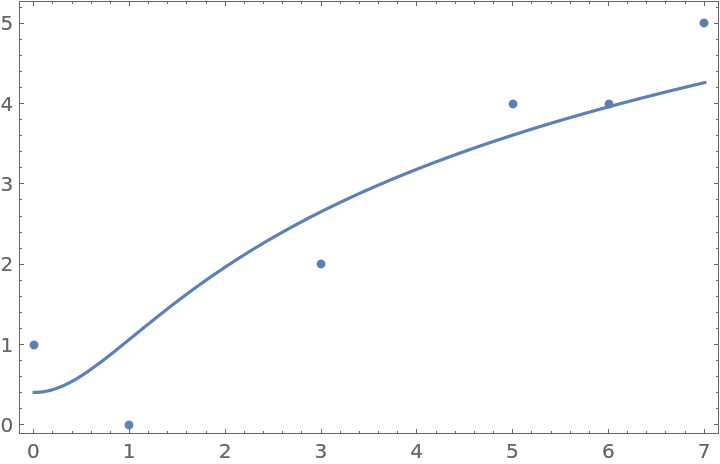 |
| In[39]:= |
| Out[39]= |  |
Generate some noisy data for three normal distributions:
| In[40]:= | ![SeedRandom[2]
amp = RandomReal[{1, 3}, 3]; x0 = RandomReal[{-3, 3}, 3]; \[Sigma] = RandomReal[{0.5, 1}, 3];
data = MapThread[
Table[{x, # Exp[-(x - #2)^2/(2 #3^2)]}, {x, Subdivide[-4, 4, 30]}] &, {amp, x0, \[Sigma]}];
data += RandomReal[{-0.3, 0.3}, {3, 31, 2}];](https://www.wolframcloud.com/obj/resourcesystem/images/647/6474b83d-a789-419f-88d3-79e5c2edc399/397d9eba24a78947.png) |
Plot the data together with their fits:
| In[41]:= | ![ResourceFunction["FittedModelPlot"][data, a Exp[-(x - b)^2/(2 c^2)], {a, b, c}, x,
PlotTheme -> {"Detailed", "NeonColor", "ThickLines", "OpenMarkersThick"},
"ErrorBands" -> True,
ConfidenceLevel -> 0.999,
PlotRange -> All,
PlotLegends -> {"A", "B", "C"}
]](https://www.wolframcloud.com/obj/resourcesystem/images/647/6474b83d-a789-419f-88d3-79e5c2edc399/7b5ecc5c0978915f.png) |
| Out[41]= | 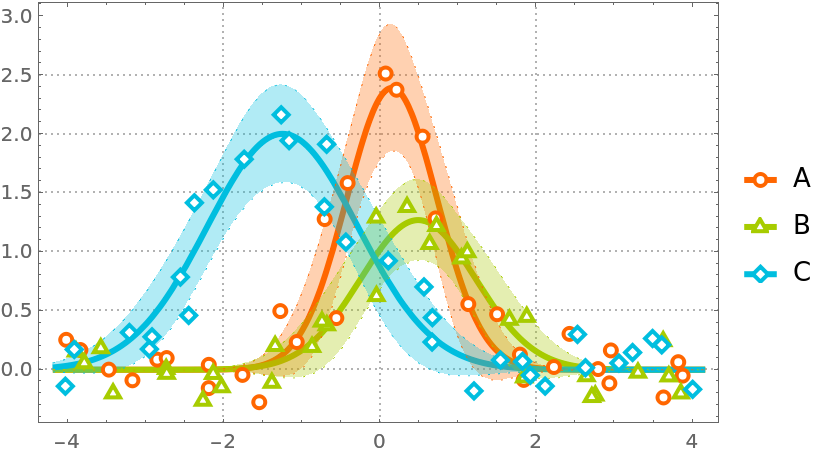 |
This work is licensed under a Creative Commons Attribution 4.0 International License