Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 FitWithErrors (1.0.0) current version: 1.0.2 »

Source Notebook

Perform linear and non-linear fits on data with error bars

Contributed by: Sjoerd Smit

ResourceFunction["FitWithErrors"][LinearModelFit[data,basis,vars]]

performs a LinearModelFit on data with Around values by finding the appropriate Weights option value based on the uncertainties in data.

ResourceFunction["FitWithErrors"][NonlinearModelFit[data,form,params,vars]]

performs a NonlinearModelFit on data with Around values.

ResourceFunction["FitWithErrors"][expr,n]

limits the algorithm to n iterations to find the weights.

Details

ResourceFunction["FitWithErrors"] is HoldFirst and inspects the given fit expression to find the correct weights.
The data is expected to be a matrix or vector input.
Only symmetric Around values are supported.
Uncertainties in the response variable of the fit are assumed to be Gaussian. The weights are computed as the inverse of the variance. Because of this, all rows of the data need to have non-zero variance.
Uncertainies in the predictor variables are accounted for using the method of Fasano & Vio (see references). This method propagates the uncertainties through the model to obtain the corresponding uncertainties in the response which are then converted to weights. The procedure is iterated several times.

Examples

Basic Examples (2) 

Fit a linear model to some data with errors in the response variable:

In[1]:=
data = {{1, Around[1, 1]}, {2, Around[0, 2]}, {3, Around[2, 0.5]}, {5, Around[4, 3]}}; lm = ResourceFunction["FitWithErrors"][ LinearModelFit[data, x, x] ]
Out[2]=
In[3]:=
Show[ Plot[lm[x], {x, 0, 6}], ListPlot[data] ]
Out[3]=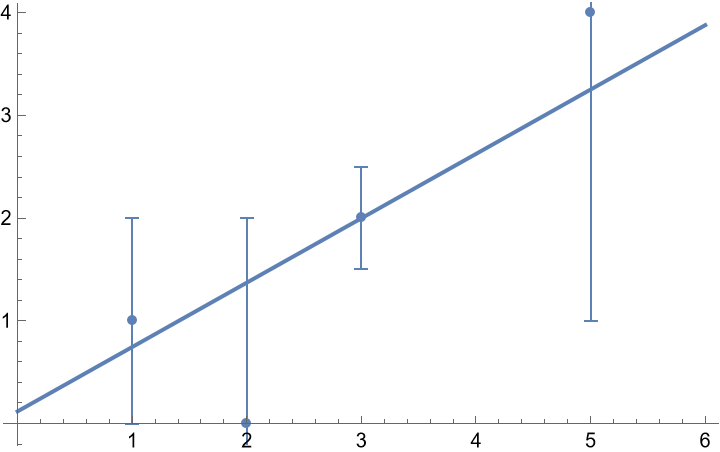

Fit data with uncertainties in both x and y:

In[4]:=
data = {{Around[1, 0.1], Around[1, 1]}, {Around[2, 1], Around[0, 2]}, {Around[3, 1], Around[2, 0.5]}, {Around[5, 1.5], Around[4, 3]}}; lm = ResourceFunction["FitWithErrors"][ LinearModelFit[data, x, x] ]
Out[5]=
In[6]:=
Show[ Plot[lm[x], {x, 0, 6}], ListPlot[data] ]
Out[6]=

Scope (1) 

Fit a NonlinearModelFit with error bars:

In[7]:=
data = {{Around[0., 0.8], Around[1., 0.8]}, {Around[1., 0.70], Around[0., 0.7]}, {Around[3., 0.4], Around[2., 0.4]}, {Around[5., 0.7], Around[4., 0.7]}, {Around[6., 0.5], Around[4., 0.5]}, {Around[7., 0.5], Around[5., 0.5]}}; nlm = ResourceFunction["FitWithErrors"] @ NonlinearModelFit[data, Log[a + b x^2], {a, b}, x]
Out[8]=
In[9]:=
Show[ListPlot[data], Plot[nlm[x], {x, 0, 7}]]
Out[9]=

Possible Issues (2) 

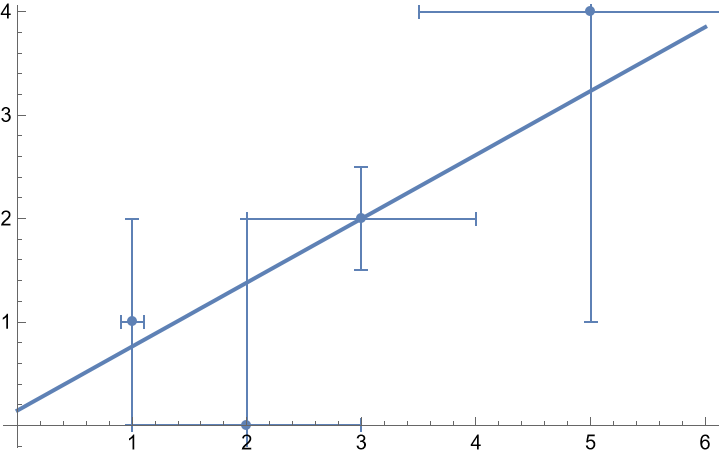If one of the rows of the input data does not have any uncertainty, it's not possible to calculate the weights for that row and the fit will fail:

In[10]:=
ResourceFunction["FitWithErrors"][ LinearModelFit[{{1, Around[1, 1]}, {2, 0}, {3, Around[2, 0.5]}, {5, Around[4, 3]}}, x, x] ]
Out[10]=

Mixing x errors with y errors does work because it's still possible to compute a weight for each row:

In[11]:=
ResourceFunction["FitWithErrors"][ LinearModelFit[{{1, Around[1, 1]}, {Around[2, 1], 0}, {3, Around[2, 0.5]}, {5, Around[4, 3]}}, x, x] ]
Out[11]=

Publisher

Sjoerd Smit

Version History

  • 1.0.2 – 21 February 2024
  • 1.0.1 – 04 October 2023
  • 1.0.0 – 02 October 2023

Source Metadata

  • Citation:
    • G. Fasano and R. Vio, "Fitting straight lines with errors on both coordinates", Newsletter of Working Group for Modern Astronomical Methodology, No. 7, 2-7, Sept. 1988.

Related Resources

License Information