Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 FirstOrderCorrelation

Source Notebook

Compute the first order correlation matrix from an original correlation matrix

Contributed by: Seth J. Chandler

ResourceFunction["FirstOrderCorrelation"][m]

computes the first order correlation matrix of a matrix m.

The matrix must be invertible.
The matrix should be symmetric and positive definite in order for the results to be useful.
Setting the option "ConditionsCheck" to True will warn if the matrix can not be confirmed to be symmetric and positive definite.

Examples

Basic Examples (2) 

Compute the first order correlation of a rational 3×3 matrix:

In[1]:=
ResourceFunction[ "FirstOrderCorrelation"][{{1, -3/5, 7/10}, {-3/5, 1, -21/50}, {7/10, -21/50, 1}}]
Out[1]=

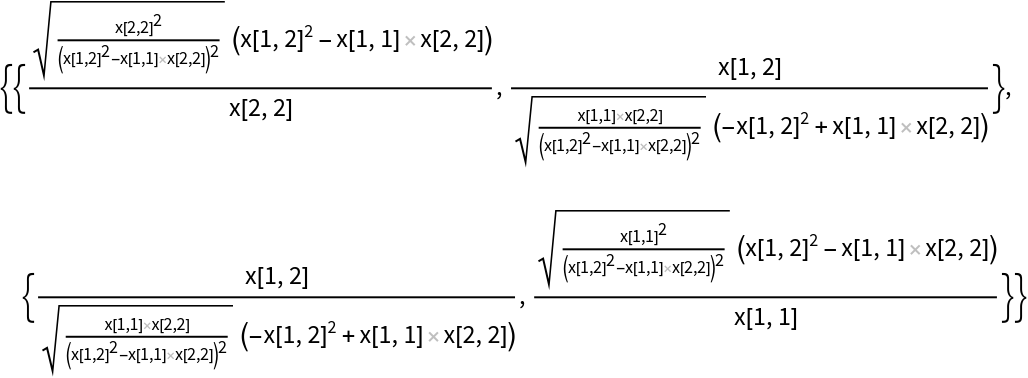
Compute the first order correlation of a symbolic symmetric 2×2 matrix:

In[2]:=
ResourceFunction["FirstOrderCorrelation"][ Array[x, {2, 2}] /. x[i_, j_] :> x[j, i] /; i > j] // FullSimplify
Out[2]=

FirstOrderCorrelation works on large matrices:

In[3]:=
ResourceFunction["FirstOrderCorrelation"][ randomMatrix]; // RepeatedTiming
Out[3]=

Unless the "ConditionsCheck" option is set to True, FirstOrderCorrelation will evaluate and provide no warning even if the matrix is not symmetric:

In[4]:=
ResourceFunction[ "FirstOrderCorrelation"][{{1, -4/5, 7/10}, {-3/5, 1, -21/50}, {7/10, -21/50, 1}}]
Out[4]=
Out[4]=

Setting "ConditionsCheck" to True also issues a warning if the matrix is not unambiguously positive definite and if it is not unambiguously positive semi-definite:

Out[4]=

Find the value of an element in a 3×3 zero-order correlation matrix that will set to 0 the corresponding element in the first order correlation matrix:

In[5]:=
Solve[0 == ResourceFunction[ "FirstOrderCorrelation"][{{1, -3/5, 7/10}, {-3/5, 1, x}, {7/10, x, 1}}][[2, 3]], x]
Out[5]=

Find the element in a 4×4 zero-order correlation matrix that will set to 0 the corresponding element in the first order correlation matrix:

In[6]:=
Solve[0 == ResourceFunction[ "FirstOrderCorrelation"][{{1, -3/5, -5/9, 7/10}, {-3/5, 1, -2/11, 3/10}, {-5/9, -2/11, 1, x}, {7/10, 3/10, x, 1}}][[3, 4]], x]
Out[6]=

The first order correlation matrix of the first order correlation matrix is the same as the original matrix:

In[7]:=
Counts[Table[ NestList[ResourceFunction["FirstOrderCorrelation"]/*Chop, Correlation[RandomVariate[NormalDistribution[0, 1], {100, 10}]], 3] // (#[[1]] - #[[3]] &)/*Chop, {100}]]
Out[7]=

The function will fail and throw a message if the matrix is singular:

Out[7]=

Compare the false positive rates and true positive rates among "minority" and "majority" populations when classifying a population where the first variable is correlated with the second, the first variable is correlated with the third, but, after the first variable is taken into account, the second variable is uncorrelated with the third.

Take a first order correlation matrix and compute the zero-order correlation matrix:

In[8]:=
m = ResourceFunction["FirstOrderCorrelation"][zeroOrderCorrelation, "ConditionsCheck" -> True]
Out[8]=
In[9]:=
zeroOrderCorrelation = ResourceFunction["FirstOrderCorrelation"][m]
Out[9]=

Use the zero-order correlation matrix as the covariance matrix of a multinormal copula and use that to produce 1000 instances of training data and 1000 instances of test data:

Classify uses AutoML to figure out how to best classify the data; ClassifierMeasurements uses the trained classifier and the test data to compute various performance statistics:

In[10]:=
cl = Classify[Map[Most][training] -> Map[Last][training], TrainingProgressReporting -> None]; ClassifierMeasurements[cl, Map[Most][test] -> Map[Last][test], {"Accuracy", "AreaUnderROCCurve" -> 1, "FalsePositiveRate" -> 1, "TruePositiveRate" -> 1}] // AssociationThread[{"Accuracy", "AreaUnderROCCurve" -> 1, "FalsePositiveRate" -> 1, "TruePositiveRate" -> 1} -> #] &
Out[10]=

Select picks out minority members from the test data set; the same performance statistics are generated:

In[11]:=
With[{minority = Select[test, #[[2]] == 1 &]}, ClassifierMeasurements[cl, Map[Most][minority] -> Map[Last][minority], {"Accuracy", "AreaUnderROCCurve" -> 1, "FalsePositiveRate" -> 1, "TruePositiveRate" -> 1}] ] // AssociationThread[{"Accuracy", "AreaUnderROCCurve" -> 1, "FalsePositiveRate" -> 1, "TruePositiveRate" -> 1} -> #] &
Out[11]=

Select picks out majority members from the test data set; the same performance statistics are generated:

In[12]:=
With[{majority = Select[test, #[[2]] == 0 &]}, ClassifierMeasurements[cl, Map[Most][majority] -> Map[Last][majority], {"Accuracy", "AreaUnderROCCurve" -> 1, "FalsePositiveRate" -> 1, "TruePositiveRate" -> 1}] ] // AssociationThread[{"Accuracy", "AreaUnderROCCurve" -> 1, "FalsePositiveRate" -> 1, "TruePositiveRate" -> 1} -> #] &
Out[12]=

Although there is no intentional "discrimination," and while the accuracy of the classifier is roughly the same for both groups, the false positive rates and true positive rates are higher for the majority than the minority.

Publisher

Seth J. Chandler

Version History

  • 1.0.0 – 29 March 2021

License Information