Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Try to find a proof of equivalence between hypergraphs in a given multiway Wolfram model system
ResourceFunction["FindWolframModelProof"][thm,axms] tries to find a proof of the hypergraph equivalence theorem thm using the multiway Wolfram model system axioms axms. |
| TimeConstraint | Infinity | how much time to allow |
| "DirectedHyperedges" | True | whether to treat hyperedges as being ordered (directed) |
Prove an elementary theorem regarding the equivalence of two hypergraphs in a simple multiway Wolfram model system:
| In[1]:= |
|
| Out[1]= |
|
Show the abstract proof network, with tooltips showing the intermediate expressions:
| In[2]:= |
|
| Out[2]= |
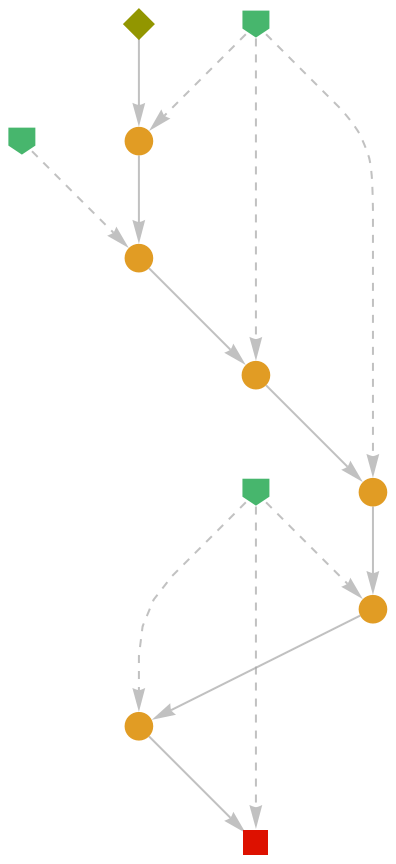
|
Show the complete list of proof steps as a Dataset object:
| In[3]:= |
|
| Out[3]= |

|
Typeset a natural language argument:
| In[4]:= |
|
| Out[4]= |

|
Prove a more sophisticated theorem involving multiple rules and hypotheses:
| In[5]:= |
![proof = ResourceFunction[
"FindWolframModelProof"][{{{1, 1, 1}} <-> {{1, 1, 1}, {1, 2, 1}, {1,
1, 2}}, {{1, 1, 1}} <-> {{1, 2, 1}, {1, 1, 1}, {1, 3, 1}, {1, 1, 3}, {2, 2, 1}, {2, 4, 2}, {1, 2, 4}}}, {{{x, x, y}} <-> {{y, y, x}, {y, z, y}, {x, y, z}}, {{x, y, x}, {z, w, y}} <-> {{w, z,
y}}}]](https://www.wolframcloud.com/obj/resourcesystem/images/f29/f29f0214-ee34-47ac-ad39-10df50bfc574/6a4b92958318fb6d.png)
|
| Out[5]= |

|
Show the abstract proof network:
| In[6]:= |
|
| Out[6]= |
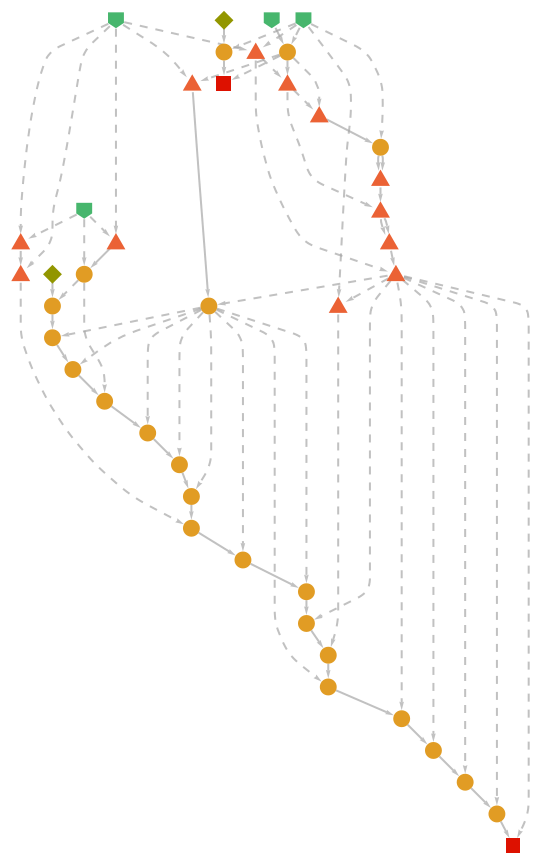
|
Theorems that are true in the case of orderless (undirected) hyperedges may not be true in the case of ordered (directed) ones:
| In[7]:= |
|
| Out[7]= |
|
| In[8]:= |
|
| Out[8]= |
|
Show that a hypergraph equivalence proposition cannot be derived from a given set of multiway Wolfram model system axioms:
| In[9]:= |
|
| Out[9]= |
|
FindWolframModelProof accepts both individual axioms and lists of axioms:
| In[10]:= |
![ResourceFunction[
"FindWolframModelProof"][{{1, 1, 1}} <-> {{1, 2, 1}, {1, 1, 1}, {1, 3, 1}, {1, 1, 3}, {2, 2, 1}, {2, 4, 2}, {1, 2, 4}}, {{x, x, y}} <-> {{y, y, x}, {y, z, y}, {x, y, z}}]](https://www.wolframcloud.com/obj/resourcesystem/images/f29/f29f0214-ee34-47ac-ad39-10df50bfc574/773f233051cd09b4.png)
|
| Out[10]= |

|
| In[11]:= |
![ResourceFunction[
"FindWolframModelProof"][{{1, 1, 1}} <-> {{1, 2, 1}, {1, 1, 1}, {1, 3, 1}, {1, 1, 3}, {2, 2, 1}, {2, 4, 2}, {1, 2, 4}}, {{{x, x, y}} <-> {{y, y, x}, {y, z, y}, {x, y, z}}, {{x, y, x}, {z, w, y}} <-> {{w, z, y}}}]](https://www.wolframcloud.com/obj/resourcesystem/images/f29/f29f0214-ee34-47ac-ad39-10df50bfc574/47887526944180dc.png)
|
| Out[11]= |

|
Likewise for theorems:
| In[12]:= |
![ResourceFunction[
"FindWolframModelProof"][{{{1, 1, 1}} <-> {{1, 2, 1}, {1, 1, 1}, {1, 3, 1}, {1, 1, 3}, {2, 2, 1}, {2, 4, 2}, {1, 2, 4}}, {{1, 1, 1}} <-> {{1, 1, 1}, {1, 2, 1}, {1, 1, 2}}}, {{{x, x, y}} <-> {{y,
y, x}, {y, z, y}, {x, y, z}}, {{x, y, x}, {z, w, y}} <-> {{w, z,
y}}}]](https://www.wolframcloud.com/obj/resourcesystem/images/f29/f29f0214-ee34-47ac-ad39-10df50bfc574/46fa3761103a2ad4.png)
|
| Out[12]= |

|
FindWolframModelProof supports single-vertex edges, ordered two-vertex edges (i.e. ordinary directed edges) and ordered three-vertex hyperedges:
| In[13]:= |
|
| Out[13]= |

|
| In[14]:= |
|
| Out[14]= |
|
| In[15]:= |
|
| Out[15]= |
|
As well as combinations of all three:
| In[16]:= |
|
| Out[16]= |
|
Use TimeConstraint→t to limit the computation time to t seconds:
| In[17]:= |
![ResourceFunction[
"FindWolframModelProof"][{{1, 1, 1}} <-> {{1, 2, 1}, {1, 1, 1}, {1, 3, 1}, {1, 1, 3}, {2, 2, 1}, {2, 4, 2}, {1, 2, 4}}, {{x, x, y}} <-> {{y, y, x}, {y, z, y}, {x, y, z}}, TimeConstraint -> 0.01]](https://www.wolframcloud.com/obj/resourcesystem/images/f29/f29f0214-ee34-47ac-ad39-10df50bfc574/323c2bcffc1381b1.png)
|
| Out[17]= |
|
By default, FindWolframModelProof looks for a proof indefinitely:
| In[18]:= |
![ResourceFunction[
"FindWolframModelProof"][{{1, 1, 1}} <-> {{1, 2, 1}, {1, 1, 1}, {1, 3, 1}, {1, 1, 3}, {2, 2, 1}, {2, 4, 2}, {1, 2, 4}}, {{x, x, y}} <-> {{y, y, x}, {y, z, y}, {x, y, z}}] // AbsoluteTiming](https://www.wolframcloud.com/obj/resourcesystem/images/f29/f29f0214-ee34-47ac-ad39-10df50bfc574/0d4747dbd85674a7.png)
|
| Out[18]= |

|
By default, all hyperedges are treated as ordered (i.e. directed):
| In[19]:= |
|
| Out[19]= |
|
Use "DirectedHyperedges"→False to treat all hyperedges as orderless (i.e. undirected):
| In[20]:= |
|
| Out[20]= |
|
FindWolframModelProof will return a proof object for a particular theorem if and only if the associated path exists in the corresponding multiway system:
| In[21]:= |
|
| Out[21]= |
|
| In[22]:= |
|
| Out[22]= |
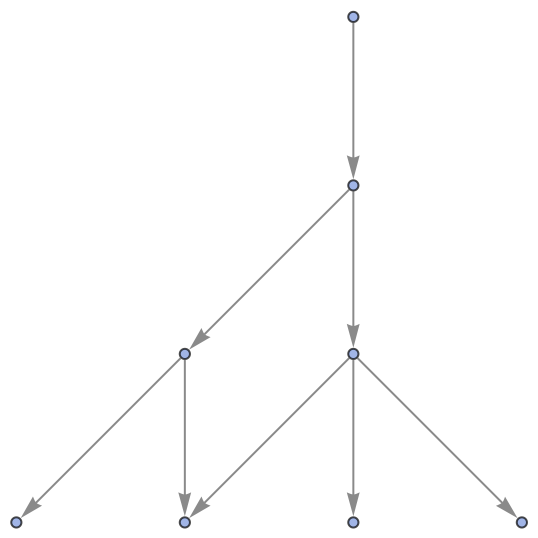
|
| In[23]:= |
|
| Out[23]= |
|
| In[24]:= |
|
| Out[24]= |
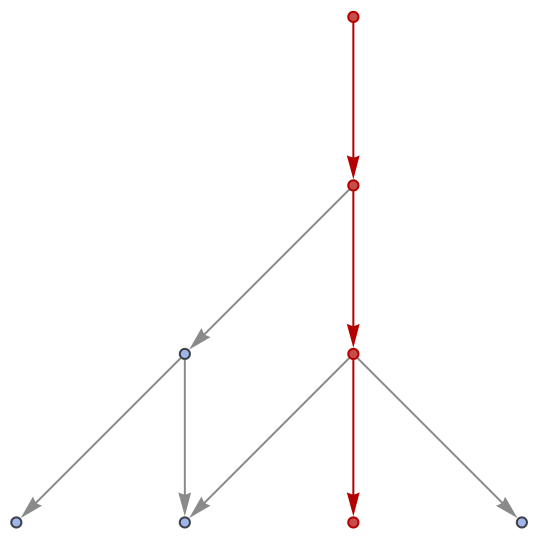
|
This work is licensed under a Creative Commons Attribution 4.0 International License