Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 FindWolframModelProof

Source Notebook

Try to find a proof of equivalence between hypergraphs in a given multiway Wolfram model system

Contributed by: Jonathan Gorard

ResourceFunction["FindWolframModelProof"][thm,axms]

tries to find a proof of the hypergraph equivalence theorem thm using the multiway Wolfram model system axioms axms.

Details and Options

If ResourceFunction["FindWolframModelProof"][thm,axms] succeeds in deriving the theorem thm from the axioms axms, then it returns a ProofObject expression. If it succeeds in showing that the theorem cannot be derived from the axioms, it returns a Failure object. Otherwise, it may not terminate unless time constrained.
ResourceFunction["FindWolframModelProof"] accepts both individual axioms and lists of axioms, and likewise for theorems.
ResourceFunction["FindWolframModelProof"] has the following options:
TimeConstraintInfinityhow much time to allow
"DirectedHyperedges"Truewhether to treat hyperedges as being ordered (directed)
If ResourceFunction["FindWolframModelProof"] exceeds the specified time constraint, it returns a Failure object.
ResourceFunction["FindWolframModelProof"][thm,axms] uses the Knuth–Bendix completion algorithm to prove that the theorem thm follows from the axioms axms.

Examples

Basic Examples (3) 

Prove an elementary theorem regarding the equivalence of two hypergraphs in a simple multiway Wolfram model system:

In[1]:=
proof = ResourceFunction[ "FindWolframModelProof"][{{1, 2}} <-> {{1, 2}, {2, 4}, {2, 3}, {3, 5}}, {{x, y}} <-> {{x, y}, {y, z}}]
Out[1]=

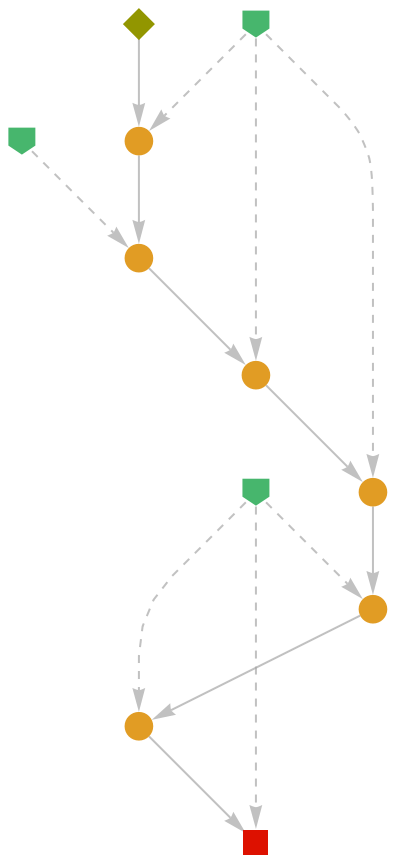
Show the abstract proof network, with tooltips showing the intermediate expressions:

In[2]:=
proof["ProofGraph"]
Out[2]=

Show the complete list of proof steps as a Dataset object:

In[3]:=
proof["ProofDataset"]
Out[3]=

Typeset a natural language argument:

In[4]:=
proof["ProofNotebook"]
Out[4]=

Prove a more sophisticated theorem involving multiple rules and hypotheses:

In[5]:=
proof = ResourceFunction[ "FindWolframModelProof"][{{{1, 1, 1}} <-> {{1, 1, 1}, {1, 2, 1}, {1, 1, 2}}, {{1, 1, 1}} <-> {{1, 2, 1}, {1, 1, 1}, {1, 3, 1}, {1, 1, 3}, {2, 2, 1}, {2, 4, 2}, {1, 2, 4}}}, {{{x, x, y}} <-> {{y, y, x}, {y, z, y}, {x, y, z}}, {{x, y, x}, {z, w, y}} <-> {{w, z, y}}}]
Out[5]=

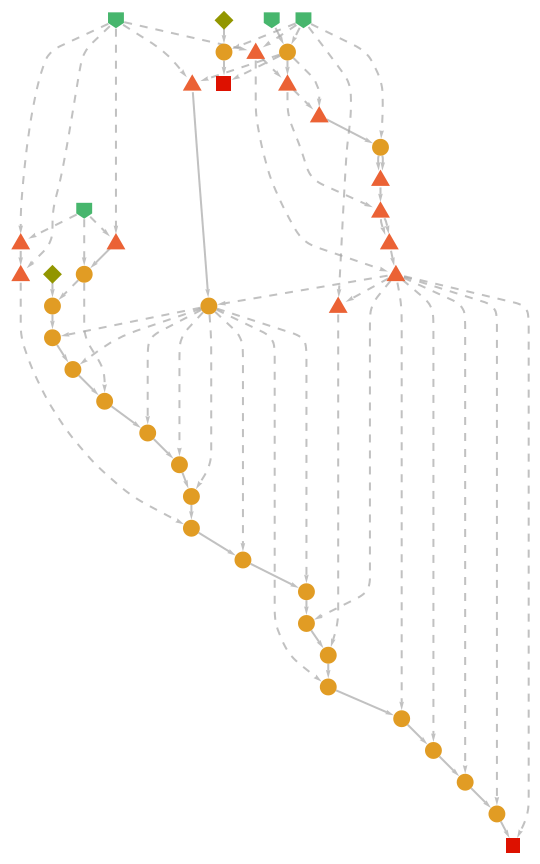
Show the abstract proof network:

In[6]:=
proof["ProofGraph"]
Out[6]=

Theorems that are true in the case of orderless (undirected) hyperedges may not be true in the case of ordered (directed) ones:

In[7]:=
ResourceFunction[ "FindWolframModelProof"][{{2, 1}} <-> {{1, 1}, {1, 2}}, {{x, y}} <-> {{x, x}, {x, y}}, TimeConstraint -> 5]
Out[7]=
In[8]:=
ResourceFunction[ "FindWolframModelProof"][{{2, 1}} <-> {{1, 1}, {1, 2}}, {{x, y}} <-> {{x, x}, {x, y}}, TimeConstraint -> 5, "DirectedHyperedges" -> False]
Out[8]=

Scope (4) 

Show that a hypergraph equivalence proposition cannot be derived from a given set of multiway Wolfram model system axioms:

In[9]:=
ResourceFunction[ "FindWolframModelProof"][{{0, 1}} <-> {{1, 2}}, {{x, y}} <-> {{y, x}}]
Out[9]=

Rules and Initial Conditions (2) 

FindWolframModelProof accepts both individual axioms and lists of axioms:

In[10]:=
ResourceFunction[ "FindWolframModelProof"][{{1, 1, 1}} <-> {{1, 2, 1}, {1, 1, 1}, {1, 3, 1}, {1, 1, 3}, {2, 2, 1}, {2, 4, 2}, {1, 2, 4}}, {{x, x, y}} <-> {{y, y, x}, {y, z, y}, {x, y, z}}]
Out[10]=
In[11]:=
ResourceFunction[ "FindWolframModelProof"][{{1, 1, 1}} <-> {{1, 2, 1}, {1, 1, 1}, {1, 3, 1}, {1, 1, 3}, {2, 2, 1}, {2, 4, 2}, {1, 2, 4}}, {{{x, x, y}} <-> {{y, y, x}, {y, z, y}, {x, y, z}}, {{x, y, x}, {z, w, y}} <-> {{w, z, y}}}]
Out[11]=

Likewise for theorems:

In[12]:=
ResourceFunction[ "FindWolframModelProof"][{{{1, 1, 1}} <-> {{1, 2, 1}, {1, 1, 1}, {1, 3, 1}, {1, 1, 3}, {2, 2, 1}, {2, 4, 2}, {1, 2, 4}}, {{1, 1, 1}} <-> {{1, 1, 1}, {1, 2, 1}, {1, 1, 2}}}, {{{x, x, y}} <-> {{y, y, x}, {y, z, y}, {x, y, z}}, {{x, y, x}, {z, w, y}} <-> {{w, z, y}}}]
Out[12]=

Types of Hyperedges (2) 

FindWolframModelProof supports single-vertex edges, ordered two-vertex edges (i.e. ordinary directed edges) and ordered three-vertex hyperedges:

In[13]:=
ResourceFunction[ "FindWolframModelProof"][{{1}, {2}} <-> {{1}, {5}, {3}, {6}, {2}, {7}, {4}, {8}}, {{x}} <-> {{x}, {y}}]
Out[13]=
In[14]:=
ResourceFunction[ "FindWolframModelProof"][{{1, 2}} <-> {{1, 2}, {2, 4}, {2, 3}, {3, 5}}, {{x, y}} <-> {{x, y}, {y, z}}]
Out[14]=
In[15]:=
ResourceFunction[ "FindWolframModelProof"][{{1, 2, 3}, {2, 3, 1}, {2, 3, 1}, {3, 1, 2}} <-> {{1, 2, 3}}, {{x, y, z}} <-> {{x, y, z}, {y, z, x}}]
Out[15]=

As well as combinations of all three:

In[16]:=
ResourceFunction[ "FindWolframModelProof"][{{1, 2, 3}, {1, 3}} <-> {{1, 2, 3}, {2, 3, 1}, {1, 2}, {2, 3}, {3}}, {{x, y, z}, {x, z}} <-> {{x, y, z}, {y, z, x}, {x, y}, {y, z}, {z}}]
Out[16]=

Options (4) 

TimeConstraint (2) 

Use TimeConstraint→t to limit the computation time to t seconds:

In[17]:=
ResourceFunction[ "FindWolframModelProof"][{{1, 1, 1}} <-> {{1, 2, 1}, {1, 1, 1}, {1, 3, 1}, {1, 1, 3}, {2, 2, 1}, {2, 4, 2}, {1, 2, 4}}, {{x, x, y}} <-> {{y, y, x}, {y, z, y}, {x, y, z}}, TimeConstraint -> 0.01]
Out[17]=

By default, FindWolframModelProof looks for a proof indefinitely:

In[18]:=
ResourceFunction[ "FindWolframModelProof"][{{1, 1, 1}} <-> {{1, 2, 1}, {1, 1, 1}, {1, 3, 1}, {1, 1, 3}, {2, 2, 1}, {2, 4, 2}, {1, 2, 4}}, {{x, x, y}} <-> {{y, y, x}, {y, z, y}, {x, y, z}}] // AbsoluteTiming
Out[18]=

DirectedHyperedges (2) 

By default, all hyperedges are treated as ordered (i.e. directed):

In[19]:=
ResourceFunction[ "FindWolframModelProof"][{{2, 1}} <-> {{1, 1}, {1, 2}}, {{x, y}} <-> {{x, x}, {x, y}}, TimeConstraint -> 5]
Out[19]=

Use "DirectedHyperedges"→False to treat all hyperedges as orderless (i.e. undirected):

In[20]:=
ResourceFunction[ "FindWolframModelProof"][{{2, 1}} <-> {{1, 1}, {1, 2}}, {{x, y}} <-> {{x, x}, {x, y}}, TimeConstraint -> 5, "DirectedHyperedges" -> False]
Out[20]=

Properties and Relations (1) 

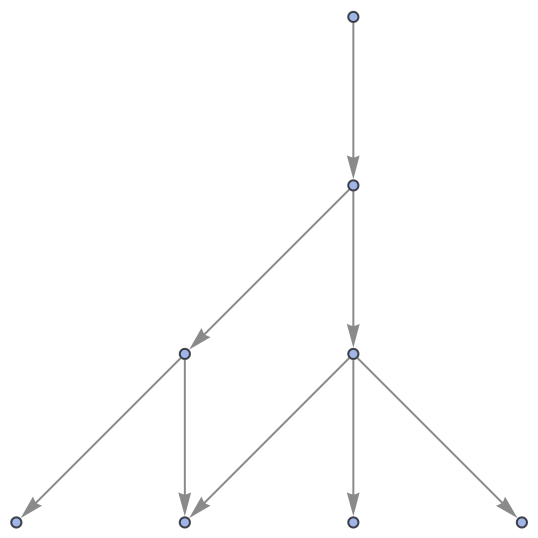
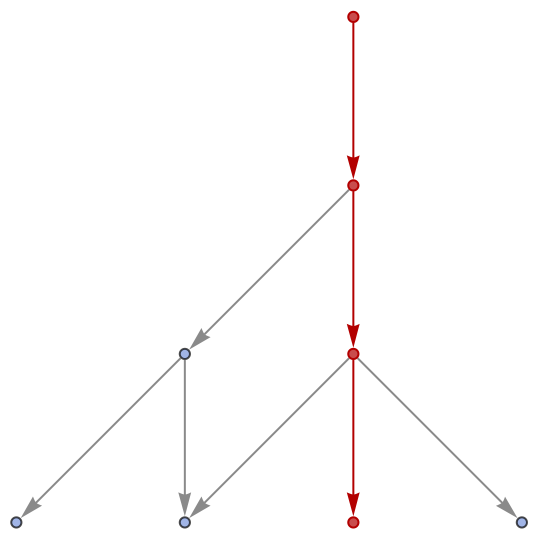
FindWolframModelProof will return a proof object for a particular theorem if and only if the associated path exists in the corresponding multiway system:

In[21]:=
ResourceFunction[ "FindWolframModelProof"][{{1, 2}} <-> {{1, 2}, {1, 3}, {4, 1}, {5, 4}}, {{x, y}} <-> {{x, y}, {y, z}}]
Out[21]=
In[22]:=
mwGraph = ResourceFunction["MultiwaySystem"][ "WolframModel" -> {{{x, y}} -> {{x, y}, {y, z}}}, {{{1, 2}}}, 3, "StatesGraphStructure"]
Out[22]=
In[23]:=
path = FindShortestPath[ mwGraph, {{1, 2}}, {{1, 2}, {1, 3}, {4, 1}, {5, 4}}]
Out[23]=
In[24]:=
HighlightGraph[mwGraph, Subgraph[mwGraph, path]]
Out[24]=

Publisher

Jonathan Gorard

Version History

  • 1.0.0 – 03 August 2020

Source Metadata

  • Citation:
    • Stephen Wolfram (2002), A New Kind of Science.
    • Stephen Wolfram (2020), "A Class of Models with the Potential to Represent Fundamental Physics".
    • Jonathan Gorard (2020), "Some Relativistic and Gravitational Properties of the Wolfram Model".
    • Jonathan Gorard (2020), "Some Quantum Mechanical Properties of the Wolfram Model".

Related Resources

License Information