Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Warning: This resource is provisional
Function Repository Resource:
Find a path that goes from one expression to another with a sequence of replacements
ResourceFunction["FindReplacePath"][theorem, axioms] finds a replacement path from the left-hand side of a theorem to its right-hand side using replacements specified by axioms. | |
ResourceFunction["FindReplacePath"][theorem,axioms,prop] return a specified property of a path. |
| "ProofObject" | corresponding ProofObject |
| "Path" | list of expressions constituting a found path (default) |
| "Justification" | list of axioms used in each subsequent step of a path together with their orientations and positions |
| "Rewrites" | list of rewriting functions that reproduce a path |
| "PathTest" | test path endpoints to match a required statement |
| "RewritesTest" | test-rewriting functions to successfully reproduce a path |
| All | all of the above as an association |
Find a replacement path given a set of equations:
| In[1]:= |
| Out[1]= |
Find a replacement path using universally quantified equations:
| In[2]:= | ![ResourceFunction["FindReplacePath"][
ForAll[{x, y}, plus[x, plus[y, 0]] == plus[x, plus[0, y]]], {ForAll[x, plus[x, 0] == x], ForAll[x, plus[x, neg[x]] == 0], ForAll[{x, y, z}, plus[plus[x, y], z] == plus[x, plus[y, z]]]}]](https://www.wolframcloud.com/obj/resourcesystem/images/a7d/a7d31233-9bf6-4fdd-a713-3d1e29307517/1896fd7bd98ef307.png) |
| Out[2]= |
| In[3]:= | ![ResourceFunction["FindReplacePath"][
ForAll[x, neg[neg[x]] == x], {ForAll[x, plus[x, 0] == x], ForAll[x, plus[x, neg[x]] == 0], ForAll[{x, y, z}, plus[plus[x, y], z] == plus[x, plus[y, z]]]}]](https://www.wolframcloud.com/obj/resourcesystem/images/a7d/a7d31233-9bf6-4fdd-a713-3d1e29307517/7ef78e1f526cc742.png) |
| Out[3]= |  |
| In[4]:= | ![ResourceFunction["FindReplacePath"][
ForAll[{a, b}, or[not[or[not[a], b]], not[or[not[a], not[b]]]] == a], {ForAll[{a, b}, and[a, b] == and[b, a]], ForAll[{a, b}, or[a, b] == or[b, a]], ForAll[{a, b}, and[a, or[b, not[b]]] == a], ForAll[{a, b}, or[a, and[b, not[b]]] == a], ForAll[{a, b, c}, and[a, or[b, c]] == or[and[a, b], and[a, c]]], ForAll[{a, b, c}, or[a, and[b, c]] == and[or[a, b], or[a, c]]]}]](https://www.wolframcloud.com/obj/resourcesystem/images/a7d/a7d31233-9bf6-4fdd-a713-3d1e29307517/399f701762175a04.png) |
| Out[4]= |  |
| In[5]:= | ![ResourceFunction["FindReplacePath"][
ForAll[{a, b, c, d}, g[a, inv[g[b, g[g[g[c, inv[c]], inv[g[d, b]]], a]]]] == d], {ForAll[{a, b, c}, g[a, g[b, c]] == g[g[a, b], c]], ForAll[a, g[a, e] == a], ForAll[a, g[a, inv[a]] == e]}] // Short](https://www.wolframcloud.com/obj/resourcesystem/images/a7d/a7d31233-9bf6-4fdd-a713-3d1e29307517/6455bb81e2c19945.png) |
| Out[5]= |
| In[6]:= | ![ResourceFunction["FindReplacePath"][
ForAll[{a, b, c}, g[g[g[a, b], c], inv[g[a, c]]] == b], {ForAll[{a, b, c}, g[a, g[b, c]] == g[g[a, b], c]], ForAll[a, g[a, e] == a], ForAll[a, g[a, inv[a]] == e], ForAll[{a, b}, g[a, b] == g[b, a]]}]](https://www.wolframcloud.com/obj/resourcesystem/images/a7d/a7d31233-9bf6-4fdd-a713-3d1e29307517/6aaf8995d2d412f5.png) |
| Out[6]= |  |
Use names from AxiomaticTheory:
| In[7]:= |
| Out[7]= | 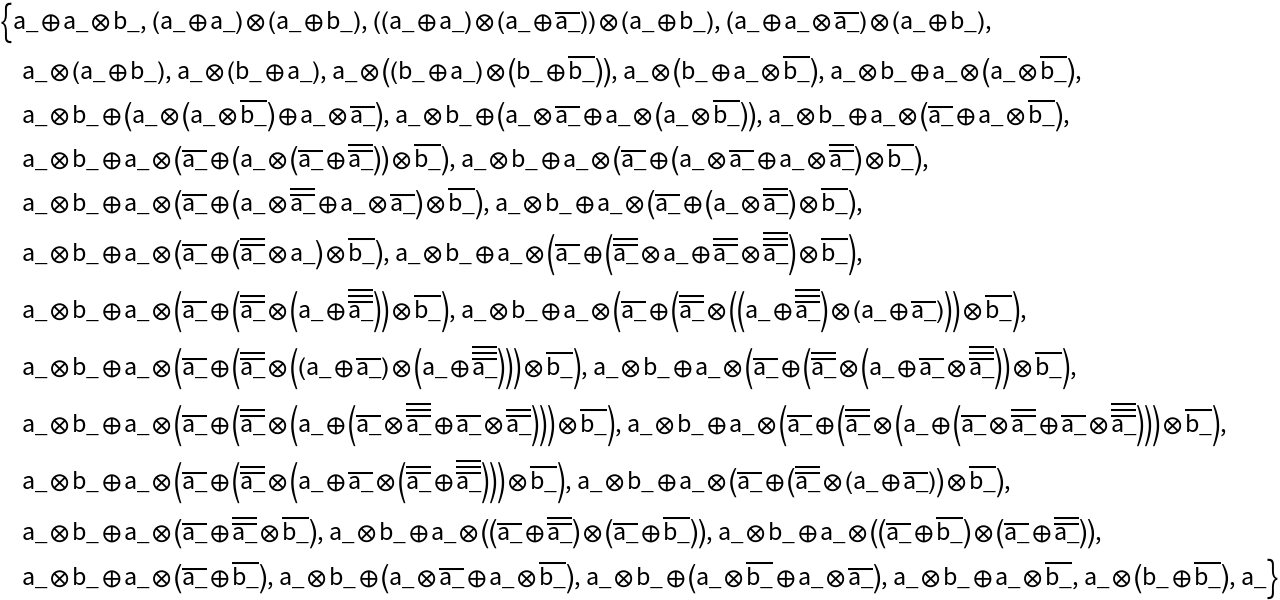 |
Use ProofObject to find a path:
| In[8]:= |
| Out[8]= |
| In[9]:= |
| Out[9]= |  |
Find a path in a string substitution system:
| In[10]:= |
| Out[10]= |
| In[11]:= |
| Out[11]= |
Find a path in a Wolfram model system:
| In[12]:= |
| Out[12]= |
| In[13]:= | ![ResourceFunction["WolframModelPlot"][#, VertexLabels -> Automatic] & /@
removeBetweenEqual@(First /@ Gather[Sort /@ (List /@ ResourceFunction["FindReplacePath"][proof, "Path"] /. {CircleMinus | CirclePlus | CircleTimes -> List,
CircleDot -> Sequence})]) // Reverse](https://www.wolframcloud.com/obj/resourcesystem/images/a7d/a7d31233-9bf6-4fdd-a713-3d1e29307517/354b4c2b245b4872.png) |
| Out[13]= | 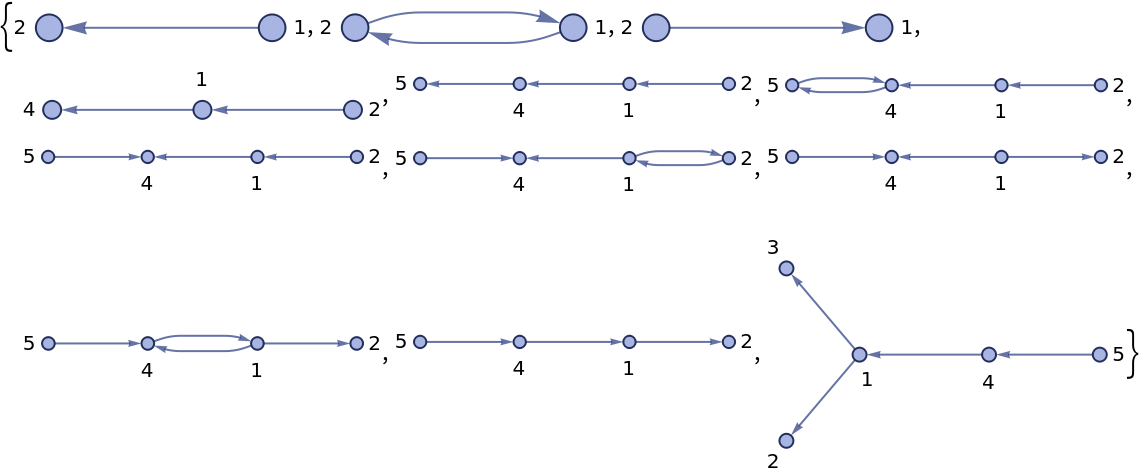 |
Reproduce the found path using rewriting functions:
| In[14]:= |
| Out[14]= |  |
| In[15]:= |
| Out[15]= | 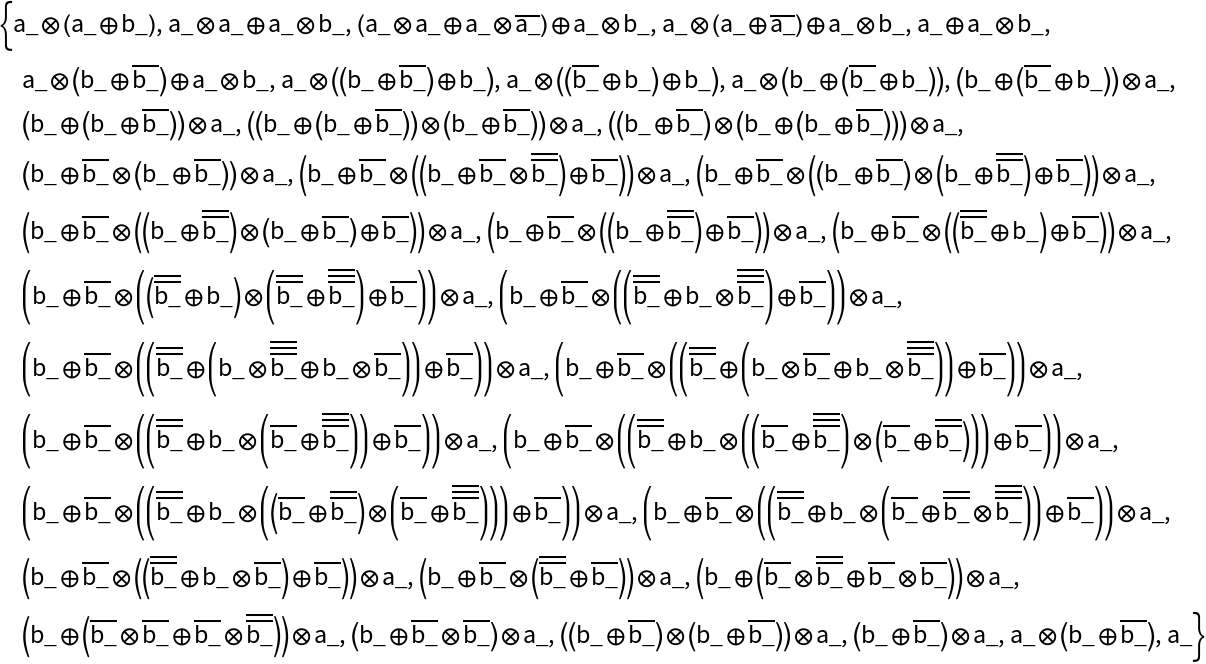 |
Degenerate axiom systems capable of deriving a==b-type statements can sometimes fail:
| In[16]:= |
| Out[16]= | 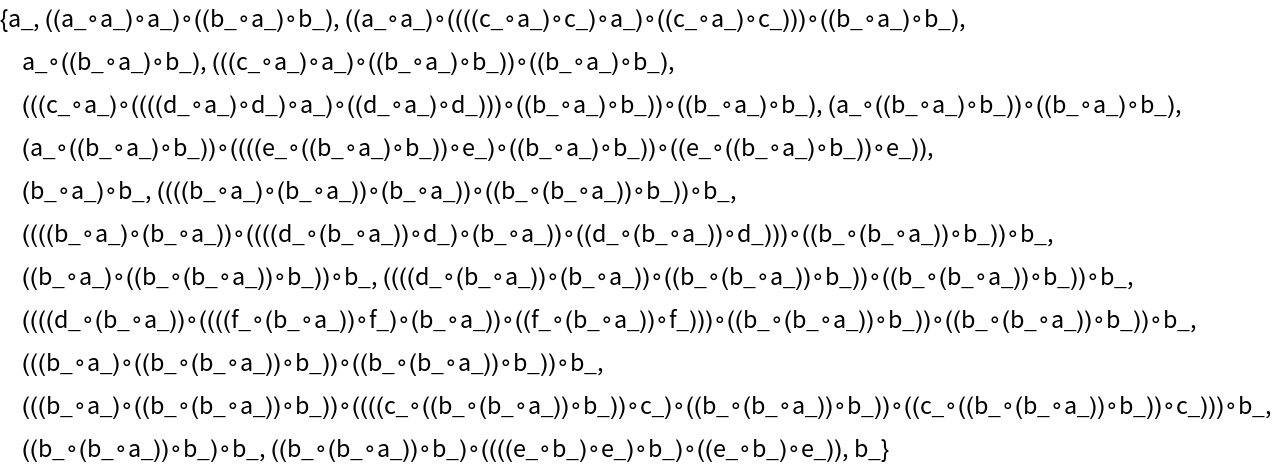 |
| In[17]:= |
| Out[17]= |  |
Test Boolean theorems:
| In[18]:= | ![AssociationMap[
ResourceFunction["FindReplacePath"][#, "BooleanAxioms", All][[{"PathTest", "RewriteTest"}]] & /@ AxiomaticTheory["BooleanAxioms", "NotableTheorems"][#] &, Keys@AxiomaticTheory["BooleanAxioms", "NotableTheorems"]]](https://www.wolframcloud.com/obj/resourcesystem/images/a7d/a7d31233-9bf6-4fdd-a713-3d1e29307517/1d583277d62b1d97.png) |
| Out[18]= | 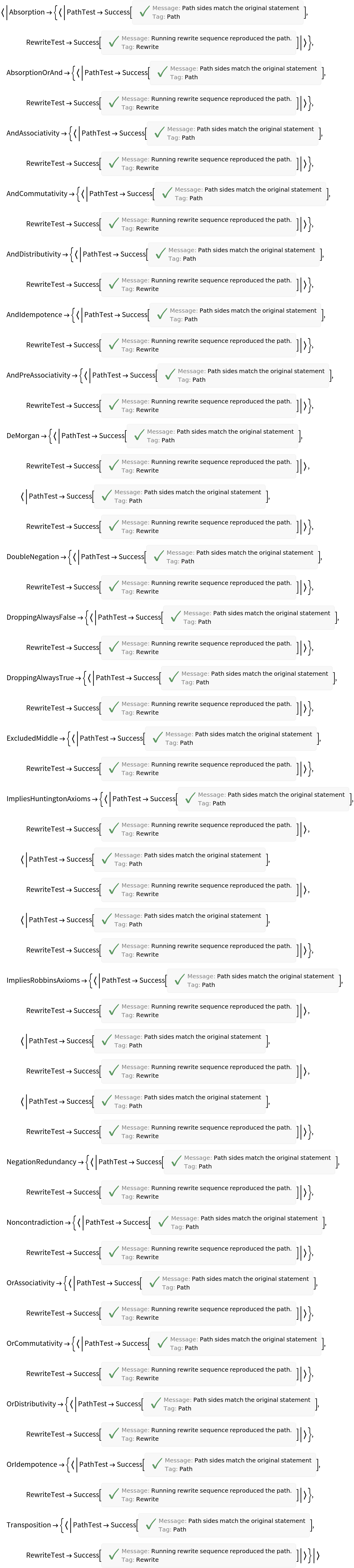 |
NKS example:

| In[19]:= | ![proof = FindEquationalProof[p\[CenterDot]q == q\[CenterDot]p, {\!\(
\*SubscriptBox[\(\[ForAll]\), \(\[FormalA]\)]\(\((\[FormalA]\[CenterDot]\[FormalA])\)\[CenterDot]\((\[FormalA]\[CenterDot]\[FormalA])\)\)\) \[Implies] \[FormalA], \!\(
\*SubscriptBox[\(\[ForAll]\), \({\[FormalA], \[FormalB]}\)]\(\[FormalA] == \((\[FormalA]\[CenterDot]\[FormalA])\)\[CenterDot]\((\[FormalA]\[CenterDot]\[FormalB])\)\)\), \!\(
\*SubscriptBox[\(\[ForAll]\), \({\[FormalA], \[FormalB]}\)]\(\[FormalA]\[CenterDot]\((\[FormalA]\[CenterDot]\[FormalB])\) == \[FormalA]\[CenterDot]\((\[FormalB]\[CenterDot]\[FormalB])\)\)\), \!\(
\*SubscriptBox[\(\[ForAll]\), \({\[FormalA], \[FormalB], \[FormalC]}\)]\(\((\[FormalA]\[CenterDot]\((\[FormalA]\[CenterDot]\((\[FormalB]\[CenterDot]\[FormalC])\))\))\) == \((\[FormalB]\[CenterDot]\((\[FormalB]\[CenterDot]\((\[FormalA]\[CenterDot]\[FormalC])\))\))\)\)\)}]](https://www.wolframcloud.com/obj/resourcesystem/images/a7d/a7d31233-9bf6-4fdd-a713-3d1e29307517/17436abb270204b6.png) |
| Out[19]= |
| In[20]:= |
| Out[20]= | 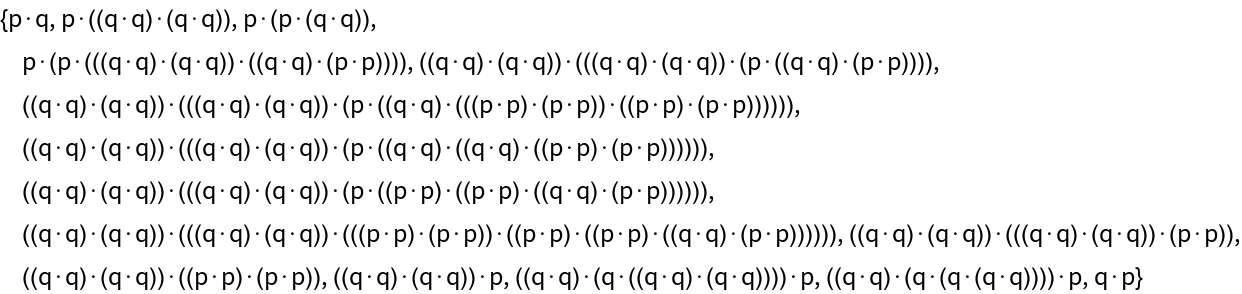 |
This result is two steps shorter than the NKS path, but it uses the reverse of one axiom:
| In[21]:= |
| Out[21]= |  |
This work is licensed under a Creative Commons Attribution 4.0 International License