Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 FindProperColorings

Source Notebook

Find all proper k-colorings of a specified graph

Contributed by: Daniel McDonald

ResourceFunction["FindProperColorings"][g,k]

finds all proper k-colorings of the graph g.

Details and Options

A proper k-coloring of a graph g is a function assigning each vertex of g one of k colors such that adjacent vertices receive distinct colors.
ResourceFunction["FindProperColorings"][g,k] gives a list of all proper k-colorings of g, where each coloring is a list whose ith element is an integer from 1,…,k representing the color assigned to the ith vertex in VertexList[g].

Examples

Basic Examples (3) 

Define a graph:

In[1]:=
g1 = Graph[{a \[UndirectedEdge] b, b \[UndirectedEdge] c, c \[UndirectedEdge] d, d \[UndirectedEdge] a, a \[UndirectedEdge] c}, VertexLabels -> "Name"]
Out[1]=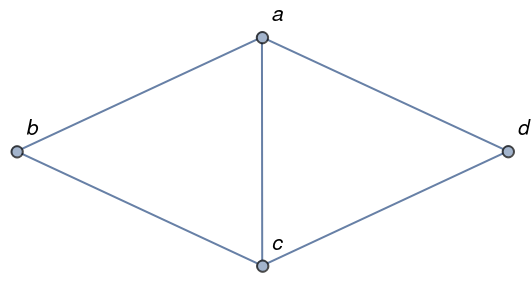

Find all its proper 3-colorings:

In[2]:=
vertexColorings = ResourceFunction["FindProperColorings"][g1, 3]
Out[2]=

Display the proper 3-colorings:

In[3]:=
showVertexColoring[g_Graph][c_List] := Graph[g, VertexLabels -> Thread[VertexList[g] -> c]] showVertexColoring[g1] /@ vertexColorings
Out[4]=

Scope (3) 

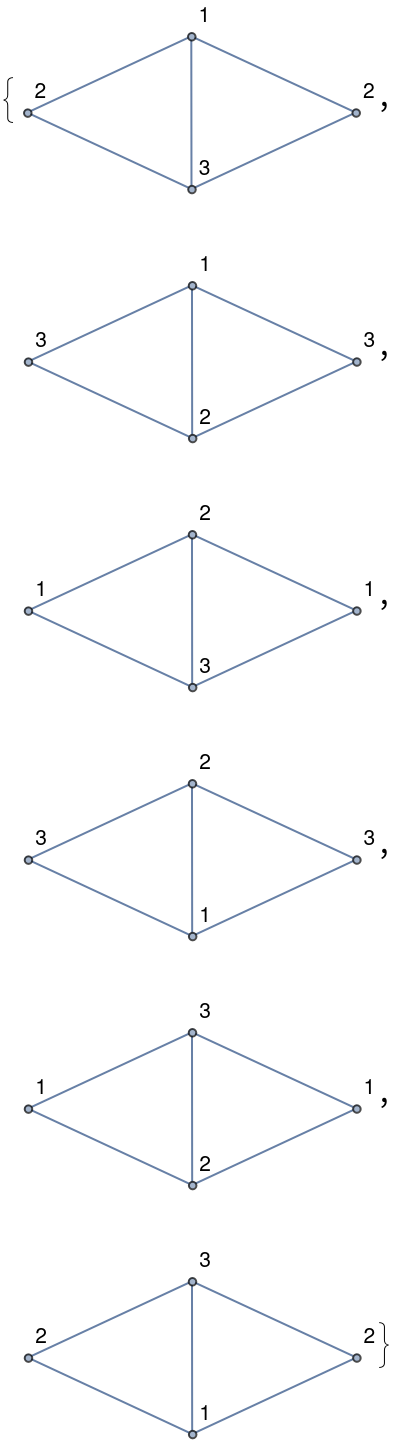FindProperColorings works on disconnected graphs:

In[5]:=
Graph[{a, b, c}, {a \[UndirectedEdge] b}, VertexLabels -> "Name"]
Out[5]=
In[6]:=
ResourceFunction["FindProperColorings"][%, 2]
Out[6]=
In[7]:=
showVertexColoring[%%] /@ %
Out[7]=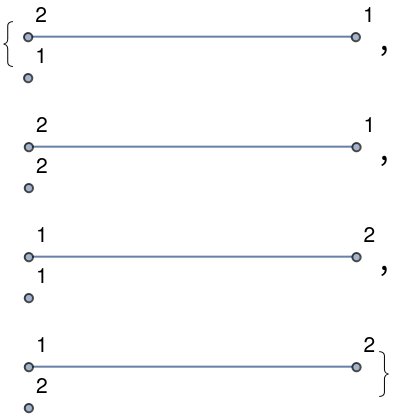

FindProperColorings works on directed graphs:

In[8]:=
Graph[{a \[DirectedEdge] b, b \[DirectedEdge] c}, VertexLabels -> "Name"]
Out[8]=
In[9]:=
ResourceFunction["FindProperColorings"][%, 3]
Out[9]=
In[10]:=
showVertexColoring[%%] /@ %
Out[10]=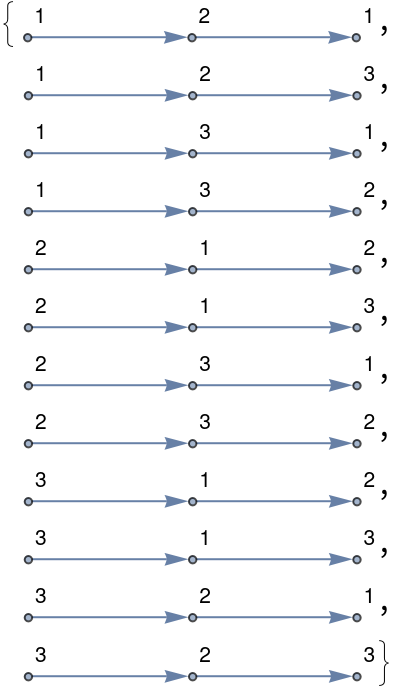

FindProperColorings works on multigraphs:

In[11]:=
Graph[{a \[UndirectedEdge] b, a \[UndirectedEdge] b}, VertexLabels -> "Name"]
Out[11]=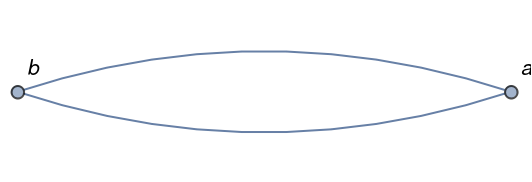
In[12]:=
ResourceFunction["FindProperColorings"][%, 3]
Out[12]=
In[13]:=
showVertexColoring[%%] /@ %
Out[13]=

Applications (4) 

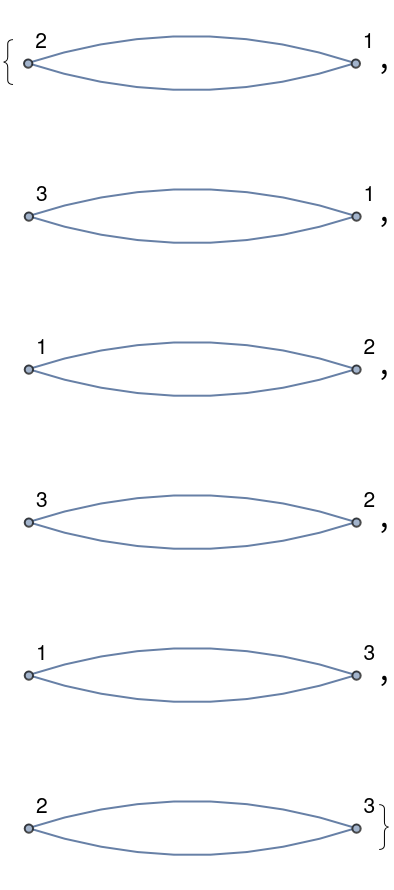Define a graph:

In[14]:=
g2 = Graph[{a \[UndirectedEdge] b, b \[UndirectedEdge] c, c \[UndirectedEdge] d, d \[UndirectedEdge] e, e \[UndirectedEdge] a, a \[UndirectedEdge] c}, VertexLabels -> "Name"]
Out[14]=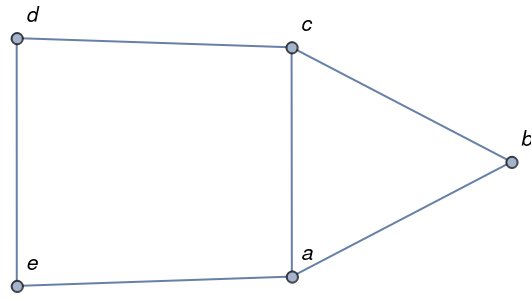

A proper k-edge-coloring of a graph g is a function assigning each edge of g one of k colors such that incident edges receive distinct colors:

In[15]:=
findProperEdgeColorings[g_Graph, k_Integer] := ResourceFunction["FindProperColorings"][LineGraph[g], k]

Find the proper 3-edge-colorings of the graph:

In[16]:=
edgeColorings = findProperEdgeColorings[g2, 3]
Out[16]=

Display the proper 3-edge-colorings:

In[17]:=
showEdgeColoring[g_Graph][c_List] := Graph[g, EdgeLabels -> Thread[EdgeList[g] -> c]] showEdgeColoring[g2] /@ edgeColorings
Out[9]=

Properties and Relations (4) 

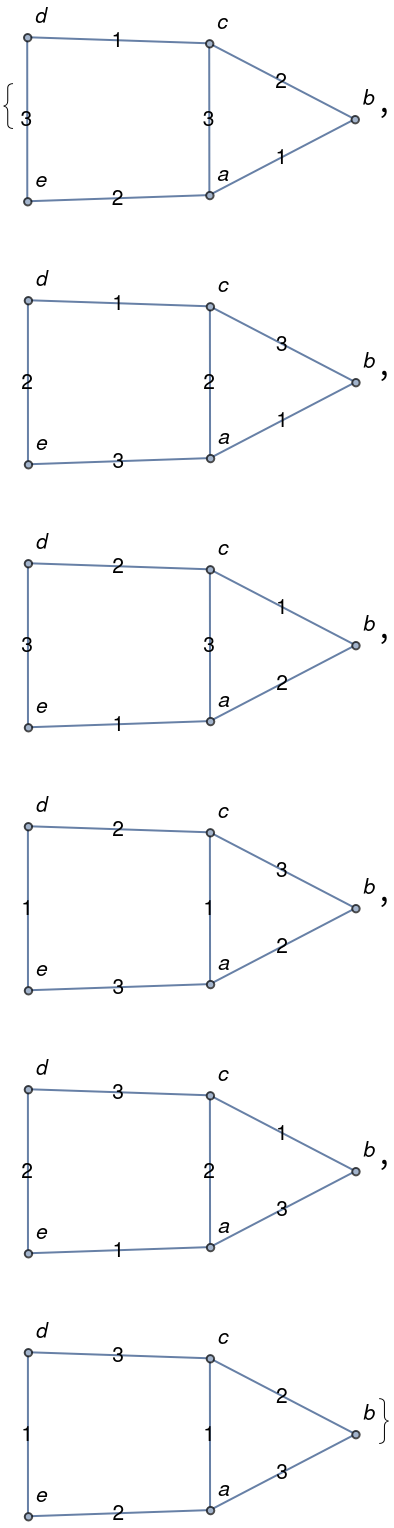Define a graph:

In[18]:=
g3 = Graph[{a \[UndirectedEdge] b, b \[UndirectedEdge] c, c \[UndirectedEdge] d, d \[UndirectedEdge] a, a \[UndirectedEdge] e}, VertexLabels -> "Name"]
Out[18]=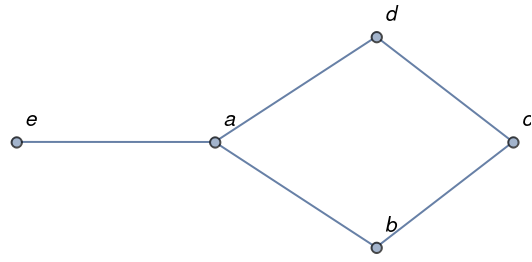

The chromatic polynomial f of a graph g is a function such that f(k) counts the proper k-colorings of g. Here is the chromatic polynomial of g3:

In[19]:=
cp = ChromaticPolynomial[g3]
Out[19]=

Use the chromatic polynomial to count the proper k-colorings of g3 for 1≤k≤5:

In[20]:=
cp /@ Range[5]
Out[20]=

Confirm that this matches the number of proper colorings returned by FindProperColorings:

In[21]:=
Table[Length[ResourceFunction["FindProperColorings"][g3, k]], {k, 5}]
Out[21]=

Publisher

Daniel McDonald

Version History

  • 1.0.0 – 16 October 2019

Related Resources

License Information