Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 FindPolygonIsometry

Source Notebook

Find an isometry in the plane that maps a polygon to a congruent one

Contributed by: Daniel McDonald

ResourceFunction["FindPolygonIsometry"][poly1,poly2]

finds an isometric transformation in the x,y-plane between congruent polygons poly1 and poly2.

ResourceFunction["FindPolygonIsometry"][poly1,poly2,n]

finds up to n isometries.

Details

An isometry is a bijective distance-preserving transformation.
Two polygons are congruent if and only if there is an isometry that maps one to the other.
An isometry is a combination of translations, rotations and reflections.
No isometry is returned if the polygons are not congruent.

Examples

Basic Examples (4) 

Find an isometry between two congruent triangles:

In[1]:=
ResourceFunction["FindPolygonIsometry"][ Triangle[{{0, 0}, {1, 0}, {0, 1}}], Triangle[{{2, 0}, {3, 0}, {2, -1}}]]
Out[1]=

Consider two congruent polygons:

In[2]:=
poly1 = RandomPolygon[5]; poly2 = TransformedRegion[poly1, RotationTransform[.4, {2, 5}]@*ReflectionTransform[{7, 2}]@* TranslationTransform[{2, 3}]]; Graphics[{Red, poly1, Blue, poly2}, Axes -> True]
Out[3]=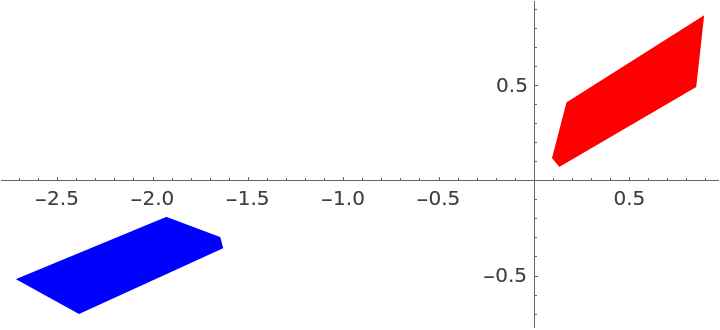

Find an isometry between them:

In[4]:=
iso = First@ResourceFunction["FindPolygonIsometry"][poly1, poly2]
Out[4]=

Apply it to the first polygon to get the second:

In[5]:=
Graphics[#, Axes -> True] & /@ {iso[poly1], poly2}
Out[5]=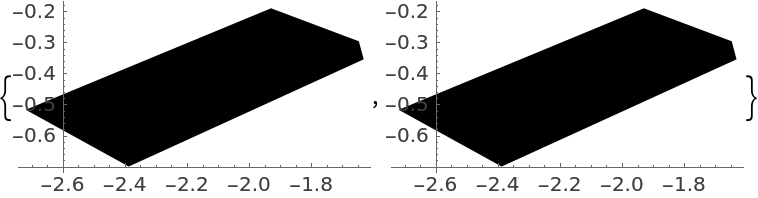

Find all eight isometries of the unit square:

In[6]:=
ResourceFunction["FindPolygonIsometry"][Rectangle[], Rectangle[], All]
Out[6]=

Define a kite:

In[7]:=
kite = Polygon[{{0, 0}, {1, 3}, {0, 4}, {-1, 3}}]; Graphics[kite]
Out[8]=

Find both of its isometries:

In[9]:=
ResourceFunction["FindPolygonIsometry"][kite, kite, All]
Out[9]=

Properties and Relations (2) 

Consider two congruent polygons with holes in them:

In[10]:=
poly1 = Polygon[{{0, 0}, {5, 0}, {2.5, 4}, {2, 1}, {2, 2}, {3, 2}, {3, 1}, {3.3, 1}, {3, 1.3}}, {1, 2, 3} -> {{4, 5, 6}, {7, 8, 9}}]; poly2 = TransformedRegion[poly1, RotationTransform[.4, {12, 5}]@*ReflectionTransform[{7, 2}]@* TranslationTransform[{2, 3}]]; Graphics[{Red, poly1, Blue, poly2}, Axes -> True]
Out[11]=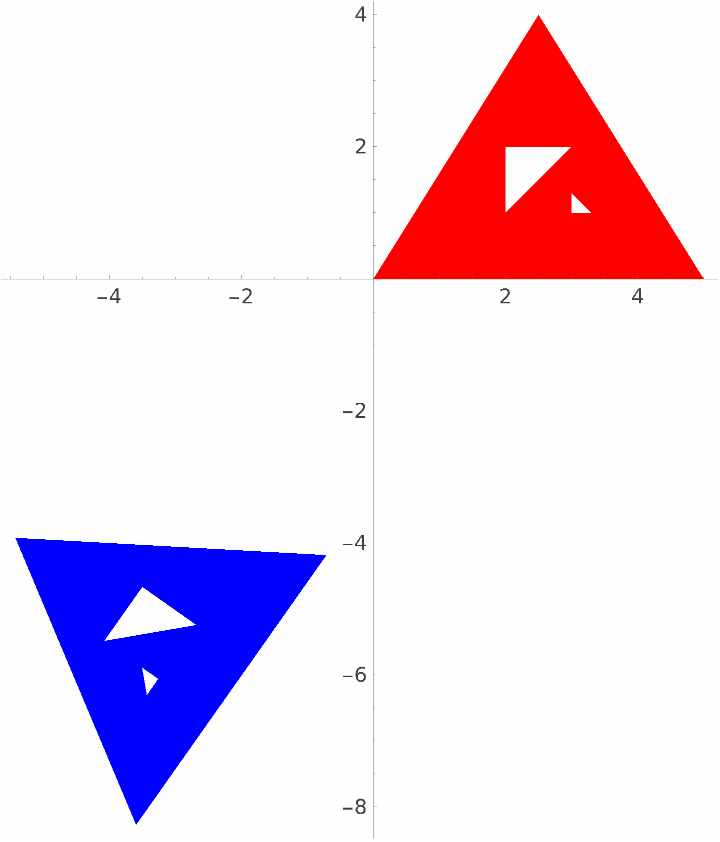

Find an isometry between them:

In[12]:=
iso = First@ResourceFunction["FindPolygonIsometry"][poly1, poly2]
Out[12]=

Apply it to the first polygon to get the second:

In[13]:=
Graphics[#, Axes -> True] & /@ {iso[poly1], poly2}
Out[13]=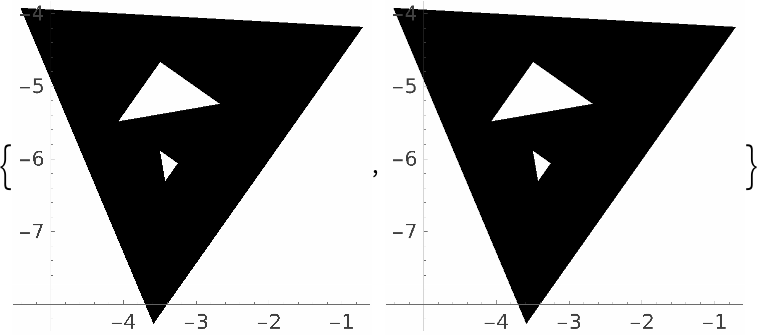

Use FindRegionTransform on the polygons:

In[14]:=
frt = FindRegionTransform[poly1, poly2]
Out[14]=

Applying this transform does not map the first polygon to the second:

In[15]:=
Graphics[#, Axes -> True] & /@ {frt[poly1], poly2}
Out[15]=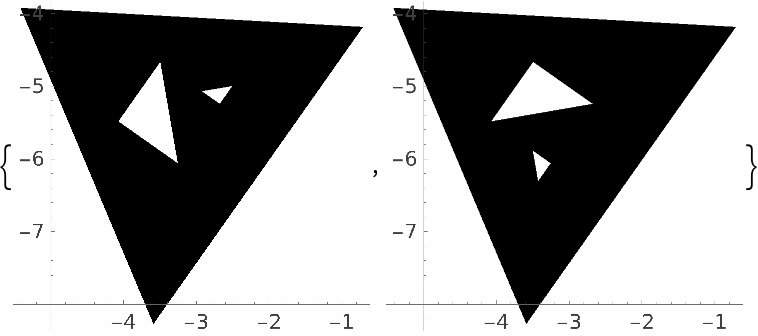

Define a function for determining polygon congruence:

In[16]:=
polygonCongruentQ[poly1_, poly2_] := MatchQ[ResourceFunction["FindPolygonIsometry"][poly1, poly2], {_}]

Consider two congruent multi-polygons:

In[17]:=
poly1 = Polygon[{{0, 0}, {5, 0}, {2.5, 4}, {2, 1}, {2, 2}, {3, 2}, {3, 1}, {3.3, 1}, {3, 1.3}}, {{4, 5, 6}, {7, 8, 9}}]; poly2 = TransformedRegion[poly1, RotationTransform[.4, {12, 5}]@*ReflectionTransform[{7, 2}]@* TranslationTransform[{-3, 5}]]; Graphics[{Red, poly1, Blue, poly2}, Axes -> True]
Out[12]=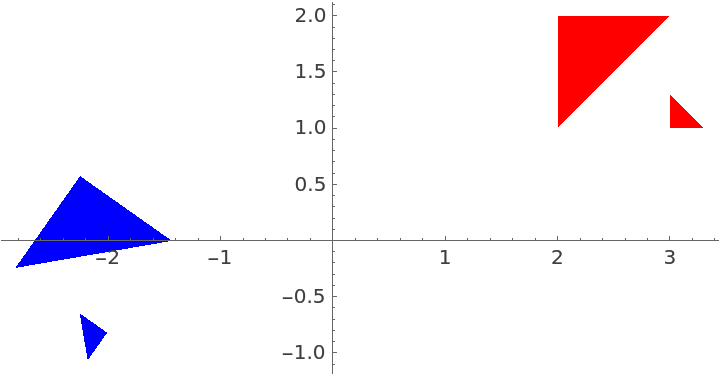

Confirm they are congruent:

In[18]:=
polygonCongruentQ[poly1, poly2]
Out[18]=

RegionCongruent does not evaluate in all cases:

In[19]:=
RegionCongruent[poly1, poly2]
Out[19]=

Possible Issues (2) 

Consider two random polygons:

In[20]:=
poly1 = RandomPolygon[5]; poly2 = RandomPolygon[5]; Graphics[{Opacity[.5], Red, poly1, Blue, poly2}, Axes -> True]
Out[21]=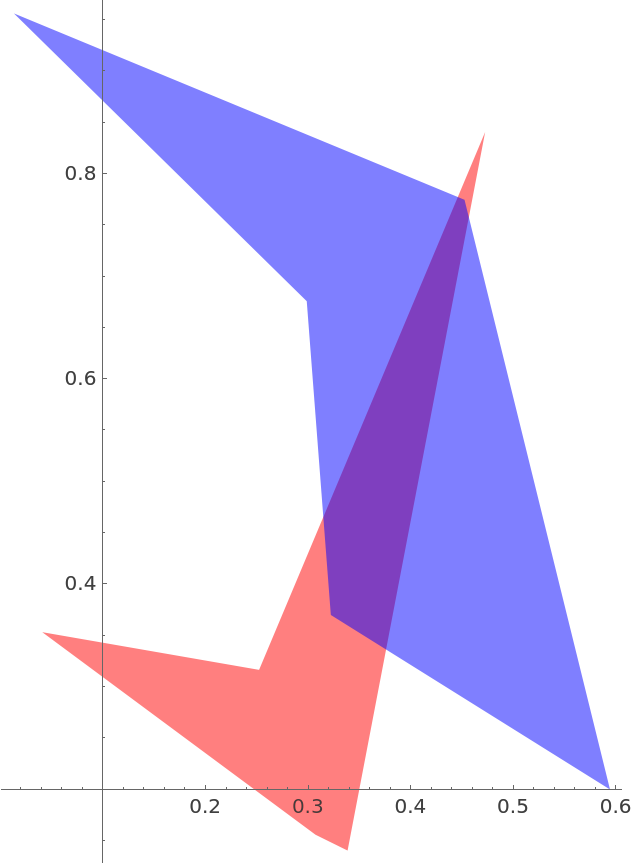

Because they are not congruent, there is no isometry between them:

In[22]:=
ResourceFunction["FindPolygonIsometry"][poly1, poly2]
Out[22]=

Publisher

Daniel McDonald

Requirements

Wolfram Language 14.0 (January 2024) or above

Version History

  • 1.0.0 – 30 July 2025

Related Resources

License Information