Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Find the longest path between two vertices in a directed acyclic graph
ResourceFunction["FindLongestPath"][g,s,t] finds the longest path from source vertex s to target vertex t in the directed acyclic graph g. | |
ResourceFunction["FindLongestPath"][{v→w,…},…] uses rules v→w to specify the graph g. |
Find the longest path from the root of a directed acyclic graph (DAG) to a leaf:
| In[1]:= |
![g = \!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, {{{1, 2}, {1, 3}, {1, 4}, {1, 5}, {1, 6}, {4, 7}, {8, 6}, {8, 7}, {8, 3}, {8, 2}, {4, 8}, {8, 9}, {4, 9}, {5, 10}}, Null}, {
GraphLayout -> {"Dimension" -> 2}, VertexLabels -> {Automatic}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGBQBWIQjQo4HGbympsuPrRi/0ll7eKvc9gd5NavCb51eNf+
jllJug812R2q9swUPTv56H7LlGV6h5exOWh8mj7B49i5/fcavpXNFmZz8KnJ
OLu+5sr+sg9BbFkFrA5P0pWkOsVu7WfZvPuO3l4Wh/d3bcQjJB7sbzlh8Ovl
T2YHWRvz1kmpj/f/NNgUN1uN2aHaj+H650/P9ie+sedydmZyiJgcKmp/88V+
I1ch9cn7GR3OtYT6hLS92v/erXPeN1NGh0dKDDXGv17vn/FxSUHuMgaH/tzQ
JXdM3u7Xck2d+12AweFaSuhRf7N3+wOap3hqvf5nv5OD4X7Pv3f7lc4t5+1Z
8dfeLDL04+Te9/tPZLG0i0T9sfcLC/2T8vj9fvfIVVsP//9lDwmXD/vTwOAb
nL/Y/9cS/19f4PzHFn1A9NmeEcpXVgKBT3D5RO5tCdzbPsD59i8n272c/A7O
37MbBF7D+ZYg4x6/gPNBuhO4n8H5xmDwGM6ft7H7un3+Azj/HH/3lMblt+Hu
Ec85KJZz8BpcXrJil6m9ziU4f0X6m0dfz5+G86fYgRx4GM5/8PLanw0eO+H8
f1pnOvlYV8D5sBQEAKIs8uo=
"]], 0.04847715736040609], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGBQBWIQjQo4HGCskPM3jr6ezw7nb/KQrNhliuCL5xwUyznI
Bue3WV5cyOCM4P/dANLACufXXVKvvaSO4HPMyzvL380C588UluUyeMIM55sY
gwCCfwWkvZYJzi+UOQ5EjHC+kCAIIPgbWaM3sEYzwPkLvnjO/+L53x7Gv3cX
BP7C+bIg4wr/wPkxG0AG/Ibz08DgG5y/2P/XEv9fX+D8xxZ9QPQZzldWAoFP
cH4i97YE7m0f4Hz7l5PtXk5+B+fv2Q0Cr+F8S5Bxj1/A+SDdCdzP4Hxw8Bg/
hvPnbey+bp//AM4/x989pXH5bTgfEl/X4HxQbNrrXILzV6S/efT1/Gk4f4od
yIGH4fwHL6/92eCxE87/p3Wmk491BZwPAwBxS4FC
"]], 0.04847715736040609], ArrowBox[{{0., 3.}, {3., 2.}}, 0.04847715736040609], ArrowBox[{{0., 3.}, {-2., 2.}}, 0.04847715736040609], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGBQBWIQjQo4HGbympsuPrTC/qSydvHXOewOcuvXBN86vMu+
Y1aS7kNNdoeqPTNFz04+am+Zskzv8DI2B41P0yd4HDtnf6/hW9lsYTYHn5qM
s+trrtiXfQhiyypgdXiSriTVKXbLnmXz7jt6e1kc3t+1EY+QeGDfcsLg18uf
zA6yNuatk1If2/802BQ3W43ZodqP4frnT8/sE9/Yczk7MzlETA4Vtb/5wt7I
VUh98n5Gh3MtoT4hba/s37t1zvtmyujwSImhxvjXa/sZH5cU5C5jcOjPDV1y
x+StvZZr6tzvAgwO11JCj/qbvbMPaJ7iqfX6n/1ODob7Pf/e2SudW87bs+Kv
vVlk6MfJve/tT2SxtItE/bH3Cwv9k/L4vb175Kqth///soeEywf7NDD4Zn8z
5GqjL98H+x3LQr1sGL7apwWHsptZfrA3n/q74vXSz/ZLftdP2Nnwwf6BYcSn
4vBP9lN9Q2VvPPlgv6Eme9tVkY/2lp5X105M/Wgf8TqrS3HPe/v+d/8dnzF9
sl9kmWPrlfbWfobt1ZtX93yyd3pyq1VV47V9iFloacLkz/amr7clb2Z8aX/o
Rr1IW9sXe1g4fUhM2Wvm+81eBhqOHBMTv1z+/N0eFs5saeU7Y6t+2j+DxsOb
B0t5rjz4ZQ+Lp92Mb9+aqf+xV4fGY+EJn9g237/21dB45jM9GnUo+J89LB1M
cQ979sryv/08aDqBJhwHWAoCAGXTEwc=
"]], 0.04847715736040609], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGCQAWIQDQEcDlCGw38wYHdYPm9j93X7//Yw+aSJRh9Ksv/Z
M0L5ejeadG80/YXL8xQvcmZs+wPn/0oEafiN4C/xByGEepu7s+TFfsL5hupW
IgknvsP5aWDwzR7mnsVg7V/g8o8t+oDoM9w9ykog8Akun8i9LYF72wc43/7l
ZLuXk9/B+Xt2g8BrON8SZNzjF3A+SHcC9zM43xgMHsPdAw6e/Adw+XP83VMa
l9+Gu0c856BYzsFrcHnJil2m9jqX4PwV6W8efT1/Gs6fYgdy4GE4/8HLa382
eOyE8/9pnenkY10B58NiDgBUO4XD
"]], 0.04847715736040609], ArrowBox[{{3., 2.}, {2., 1.}}, 0.04847715736040609], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGCQAWIQDQEcDlCGg9mdKz1cyRwOk9zDnr2y/G9fmTr3ktw1
Dgc+06NRh4L/2Z+YHXnRJpLToeiET2yb7197pXrOzpQ3nA57GN++NVP/Y9/F
v/bn1H4uh7cPlvJcefDL/q+Pi/JFJ24H9rTynbFVP+1rzM+zirHxOHBMTPxy
+fN3e47zvgtTbvI4fEpM2Wvm+81+vvCBr3v28DoculEv0tb2xf5aSuhRfzM+
h9QuFT+1+s/2JomiwlMX8jnc7xWyfZv9yX4XB8P9nn98DvqPPR/e8vlonxwt
qmnuy+8Q0nXK6r3iB3vTyNCPk3v5HeazaU4OufbWXp/pgPni/fwOTnP8pSUC
X9v7hYX+SXnM7zDxKgef5pYX9lNCRe1v/uB36NkUkt3+/6k9JFgEHIzB4DGc
P29j93X7/Adw/jn+7imNy2/bM0L54jkHxXIOXoPLS1bsMrXXuQTnr0h/8+jr
+dNw/hS7l5PtXh6G8x+8vPZng8dOOP+f1plOPtYVcD4s5gCR0qTK
"]], 0.04847715736040609], ArrowBox[{{-2., 2.}, {-2., 1.}}, 0.04847715736040609], ArrowBox[{{2., 1.}, {-1., 0.}}, 0.04847715736040609], ArrowBox[{{2., 1.}, {0., 0.}}, 0.04847715736040609], ArrowBox[{{2., 1.}, {2., 0.}}, 0.04847715736040609], ArrowBox[{{2., 1.}, {3., 0.}}, 0.04847715736040609], ArrowBox[{{2., 1.}, {4., 0.}}, 0.04847715736040609]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {DiskBox[{0., 3.}, 0.04847715736040609], InsetBox["1", Offset[{2, 2}, {0.04847715736040609, 3.048477157360406}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{-1., 0.}, 0.04847715736040609], InsetBox["2", Offset[{2, 2}, \
{-0.9515228426395939, 0.04847715736040609}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{0., 0.}, 0.04847715736040609], InsetBox["3", Offset[{2, 2}, \
{0.04847715736040609, 0.04847715736040609}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{3., 2.}, 0.04847715736040609], InsetBox["4", Offset[{2, 2}, {3.048477157360406, 2.048477157360406}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{-2., 2.}, 0.04847715736040609], InsetBox["5", Offset[{2, 2}, {-1.9515228426395939, 2.048477157360406}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{2., 0.}, 0.04847715736040609], InsetBox["6", Offset[{2, 2}, {2.048477157360406, 0.04847715736040609}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{3., 0.}, 0.04847715736040609], InsetBox["7", Offset[{2, 2}, {3.048477157360406, 0.04847715736040609}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{2., 1.}, 0.04847715736040609], InsetBox["8", Offset[{2, 2}, {2.048477157360406, 1.0484771573604061}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{4., 0.}, 0.04847715736040609], InsetBox["9", Offset[{2, 2}, {4.048477157360406, 0.04847715736040609}],
ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}, {DiskBox[{-2., 1.}, 0.04847715736040609], InsetBox["10", Offset[{2, 2}, \
{-1.9515228426395939, 1.0484771573604061}], ImageScaled[{0, 0}],
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{
"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{217.95703125, Automatic}]\);](https://www.wolframcloud.com/obj/resourcesystem/images/f83/f83b39a2-ac8f-4fae-8c4f-638534efd2b2/211dec4e0c024214.png)
|
| In[2]:= |
|
| Out[2]= |
|
Highlight the longest path:
| In[3]:= |
|
| Out[3]= |
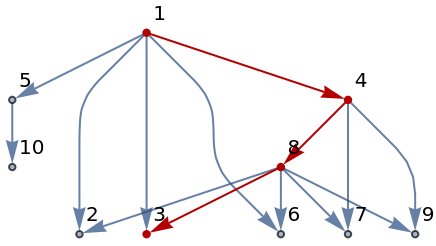
|
FindLongestPath works with directed acyclic graphs:
| In[4]:= |
![g = \!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{"A", "B", "C", "D", "E", "F", "G", "H"}, {{{1, 2}, {1, 3}, {2, 3}, {2, 4}, {3, 4}, {2, 5}, {4, 5}, {4, 6}, {4, 7}, {3, 7}, {5, 8}, {6, 8}, {7, 8}}, Null}, {
GraphLayout -> {
"LayeredDigraphEmbedding", "Orientation" -> Left}, VertexLabels -> {
Placed["Name", Center]}, VertexSize -> {Medium}}]]},
TagBox[GraphicsGroupBox[{
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[Medium], ArrowBox[{{-4.999999999999998, 1.339744851455892*^-7}, {-3.9999999999999987`, 1.0717958811647137`*^-7}}, 0.09999999999999999], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGCQAWIQ/e8/CAgfqK3dwBHyu9HuqV/9zqpzwgc4Jr5asfzQ
CvscncZpH6YIH2D4zdd+5/Au+6kzWKcnBgsfcDkzW/vc5KP2MZN5dp/lFD4w
cUL5Is9j5+yPyExjMt0hdMAolTdkQ80V+zMmi3KnxwkduLfHaV6n2C374tsG
f778ETyw4vnb8AiJB/a7BZzW+U4WPODol3NkUupj+8VXrjYvVBQ8YDtpjsiX
T8/sm9cqTzp5X+CABTdrkP3NF/a3BI/7/p4lcGBuJ29HSNsr+5WMB7aZBQsc
yOXdts3412v71zV8Z6s5BA4smvbv7h2Tt/Z+7KmKU0v5DzipPv/rb/bOfp12
BLPbFb4D3jvzxXr/vbP/m/bNnkuX78CeoBnqU3rf21vutL/+sJ73wLSPCYap
j9/bJymZnDxzhufAm1NPJBkYPtj/cfT6dF6a54DfKlcwf8L2H3ofSrgPNC5c
LwHiSzXb1+ve4DrQuEEJzJ+1RO5xuyvXAb/r88RBfAGZaVH/93AeeCOqAuY3
vFz6dLId54HwnE1iIP5THr8W11McBybc8gTzndv6zEQSOA7MSHglCuJPC03/
8/8/+4H8f5PBfAA8zNh/
"]], 0.09999999999999999], ArrowBox[{{-3.9999999999999987`, 1.0717958811647137`*^-7}, {-2.999999973205102, 1.0000000803846907`}}, 0.09999999999999999], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGCQAWIQ/fc/CPAfSEqScgw+WmMXeP7G0dfz+Q8kq+8S/5hX
Y7feQ7Jilyn/AWXGJ/Ll/DV2ojkHxXIO8h1Y8H565NNl1XbNlhcXMjjzHbjx
6eoRa9Nqu18bQBp4D5zjmpdYtavKrvqSeu0ldd4DTeYf9BeaVdmxzMs7y9/N
c+BDxRn9DSsr7aYJy3IZPOE+IHveKHG5cKWdoTEIcB9gs1I+0lZSYXcepL2W
64Dv+hv2ty6U2xXKHAcizgPTVPp26+qW2wkIggDngfsznc0bO8vs1rFGb2CN
5jigxv9z05WnpXZ+v5b4/1rCfiCvZZ2ehlOp3TswYDuw7Wfyqup5JXa9jy36
HluwHfibJ6l2/lexne6NJiBiPeD25NxCpfBiuzNgwHKgN7JFtmxzkV3qm0df
z0uzHCg7UtIQKlJk9zNxotGHEuYDi6Rub/SpK7RrBhvAdEAoZvvG6I8Fdkz+
25+1uzIdONLB2dCUW2BXeUwv7v8exgOljostm57m272YbPdysh3jgWfu8gL6
TPl2viDlpxgO3Fdpb+Y2zLNbbaBuJZLAcCDuxq3J4kW5dpD4+r8fEl85dgC9
w9Ws
"]], 0.09999999999999999], ArrowBox[BezierCurveBox[CompressedData["
1:eJwdx2tIk3EYhvFXbe6gbVopYkJU6pRwS1eKIqIJiX1wmEMxA8eaQpZWyKyl
wy9RgiXhKrGZWyZbgukwiyjkedhyYkVBTklza8ucp9zm5iFPW/274eLmd1hy
5WxFIEVRcf8iv+sn46BEEp1TNNyQhT0ltWsdHOTF9unUhufAmzYk2RM5mKkv
V34zvoXcthy+UctGXtGR9E/KYdiZGruu2s/GjK1Tb/JMn0Gsk9Orru7FbkfT
hf4GM1zaSbHyhkKRWzky0BQ5BTFT/u2FzRAcVzh/lUTZoC7bJlbFh+CjMamo
tWIG6vjm0NxcFhYPmnRejwNK+ZZEJTBx3zBjLmtyHmKrbj1dP8nEzkTqkOj2
Inz/MVpbrWWgx94rFGwtwY37LzQbYQyMdLLl0yeWwVfPT3goo+OegniVMNUJ
NV1C1mlzMBoCvK/u+pxgCmLnsZKC8QxTNqq85wKmpspqb6ShRto7Lp1xwWPL
x1SBIAgjOuQWv98F6V8jJriKQIxZQyvxpKlcFjMSgHEFDBux/F3PgfDwADyu
E9qJo/Tel7QyCtOotp/ENfn12tV8P2SXWmeI+1I4sxbLLuQPxM0SLx18dnTk
2g4UhlQ7iI/R0iR62jackw7OEV90ftC0t2+CZGh7nlidtOFRp/0BlS99kdgY
JbpsW1iHjLDKJeKJfntomX4NMj2Nv4nHPWozp3kVOrvvLBO/t7cYfXIvSLkK
J3FXQ98kV+GBlptiF3G10RfZ/GAFojuT3cTc1431CegGVqv7v7+IkukU5Ybz
xU9WiP8CiERiEw==
"]], 0.09999999999999999], ArrowBox[{{-2.999999973205102, 1.0000000803846907`}, {-1.9999999999999993`, 5.3589794058235685`*^-8}}, 0.09999999999999999], ArrowBox[BezierCurveBox[CompressedData["
1:eJxTTMoPSmViYGCQAWIQPS00/c///+wH8v9NFmVg+GD/SsXh0Ov57Adc59iC
+R7zGkp2mbIf8FO6JwLirzuoIZxzkO1Ax4RSMF+m32IegzPbgc/PmMH8KWwb
RCt2sR6YoNopDOKLaPRXXlJnPRDnwwrmz/189SR/N8uBuOgKIRDfILOFzeAJ
84EJQY8EQfxTHbP0jY2ZD3wydAbzM2qfnFOvZTqQ1zpfAMTnKNLLkznOeODl
jd/8IP7KtApeQUHGA2k6EWC+e/ShNazRDAce1m/hA/HPzJeY8cXz//7YywJg
Pk/nmmt37/7df1MtlxfE9ypyED1e+Gd/SNVJHhC/I/pK8AbW3/svnFUF84+5
ZEyaOfPnfh/FJm4Q/0/zlCfzzX/sX8/wmAvEV8j/GPvg5bf9D7/7gPnGbPX/
ojZ83f+Q7QAniG/iaXuMv/vL/nW6NmC+soXO1n+Vn/d75xzkAPEZLnufVq/9
tH/bIX8w/4zkHI7uKR/3fzB4zg7it/HI5moc+LD/x7Z2MD8mbO7H///f7z8f
YgjmAwBfZMKG
"]], 0.09999999999999999], ArrowBox[{{-1.9999999999999993`, 5.3589794058235685`*^-8}, {-1.0000000267948967`, \
-0.9999999732051026}}, 0.09999999999999999], ArrowBox[{{-1.9999999999999993`, 5.3589794058235685`*^-8}, {-0.9999999999999997, 2.6794897029117842`*^-8}}, 0.09999999999999999], ArrowBox[{{-1.9999999999999993`, 5.3589794058235685`*^-8}, {-0.9999999732051026, 1.0000000267948967`}}, 0.09999999999999999], ArrowBox[{{-1.0000000267948967`, -0.9999999732051026}, {0.,
0.}}, 0.09999999999999999], ArrowBox[{{-0.9999999999999997, 2.6794897029117842`*^-8}, {
0., 0.}}, 0.09999999999999999], ArrowBox[{{-0.9999999732051026, 1.0000000267948967`}, {0., 0.}}, 0.09999999999999999]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[
0.7]}], {
DiskBox[{-4.999999999999998, 1.339744851455892*^-7}, 0.09999999999999999], InsetBox["\<\"A\"\>", {-4.999999999999998, 1.339744851455892*^-7},
BaseStyle->"Graphics"]}, {
DiskBox[{-3.9999999999999987, 1.0717958811647137*^-7}, 0.09999999999999999], InsetBox["\<\"B\"\>", {-3.9999999999999987, 1.0717958811647137*^-7},
BaseStyle->"Graphics"]}, {
DiskBox[{-2.999999973205102, 1.0000000803846907}, 0.09999999999999999], InsetBox["\<\"C\"\>", {-2.999999973205102, 1.0000000803846907},
BaseStyle->"Graphics"]}, {
DiskBox[{-1.9999999999999993, 5.3589794058235685*^-8}, 0.09999999999999999], InsetBox["\<\"D\"\>", {-1.9999999999999993, 5.3589794058235685*^-8},
BaseStyle->"Graphics"]}, {
DiskBox[{-1.0000000267948967, -0.9999999732051026}, 0.09999999999999999], InsetBox["\<\"E\"\>", {-1.0000000267948967, -0.9999999732051026},
BaseStyle->"Graphics"]}, {
DiskBox[{-0.9999999999999997, 2.6794897029117842*^-8}, 0.09999999999999999], InsetBox["\<\"F\"\>", {-0.9999999999999997, 2.6794897029117842*^-8},
BaseStyle->"Graphics"]}, {
DiskBox[{-0.9999999732051026, 1.0000000267948967}, 0.09999999999999999], InsetBox["\<\"G\"\>", {-0.9999999732051026, 1.0000000267948967},
BaseStyle->"Graphics"]}, {DiskBox[{0., 0.}, 0.09999999999999999], InsetBox["\<\"H\"\>", {0., 0.},
BaseStyle->"Graphics"]}}}],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{
"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FormatType->TraditionalForm,
FrameTicks->None,
ImageSize->{288., Automatic}]\);](https://www.wolframcloud.com/obj/resourcesystem/images/f83/f83b39a2-ac8f-4fae-8c4f-638534efd2b2/16a4e2699c79ee6a.png)
|
| In[5]:= |
|
| Out[5]= |
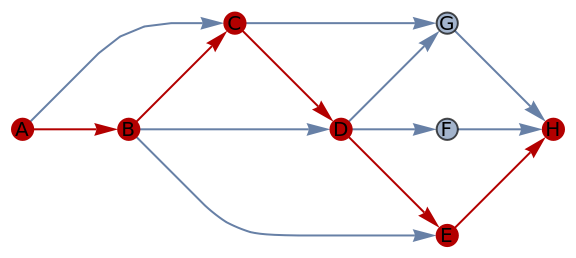
|
Use rules to specify the graph:
| In[6]:= |
|
| In[7]:= |
|
| Out[7]= |
|
| In[8]:= |
|
| Out[8]= |
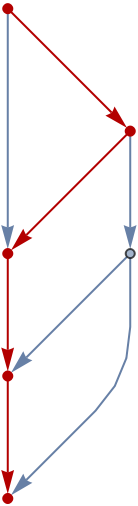
|
FindLongestPath is left unevaluated if the input graph is not a DAG:
| In[9]:= |
![ResourceFunction["FindLongestPath"][\!\(\*
GraphicsBox[
NamespaceBox["NetworkGraphics",
DynamicModuleBox[{Typeset`graph = HoldComplete[
Graph[{1, 2, 3, 4, 5}, {{{1, 2}, {2, 3}, {3, 4}, {4, 5}, {3, 5}}, {{3, 1}}}, {
EdgeStyle -> {
Arrowheads[0.08]}, ImageSize -> 120, VertexSize -> {4 -> Medium, 1 -> Medium}}]]},
TagBox[GraphicsGroupBox[
GraphicsComplexBox[{{2.017540427513767, 0.000442083090181955}, {2.017313637850549, 0.8021720908379496}, {1.0081041532060644`, 0.4011713309635613}, {0., 0.}, {0.00022442849777104534`, 0.8026134053739986}}, {
{Hue[0.6, 0.7, 0.5], Opacity[0.7], Arrowheads[0.08], LineBox[{1, 3}], ArrowBox[{1, 2}], ArrowBox[{2, 3}], ArrowBox[{3, 4}], ArrowBox[{3, 5}], ArrowBox[{4, 5}]},
{Hue[0.6, 0.2, 0.8], EdgeForm[{GrayLevel[0], Opacity[0.7]}], DiskBox[1, 0.08017300398243705], DiskBox[2, 0.02275362775597045], DiskBox[3, 0.02275362775597045], DiskBox[4, 0.08017300398243705], DiskBox[5, 0.02275362775597045]}}]],
MouseAppearanceTag["NetworkGraphics"]],
AllowKernelInitialization->False]],
DefaultBaseStyle->{
"NetworkGraphics", FrontEnd`GraphicsHighlightColor -> Hue[0.8, 1., 0.6]},
FrameTicks->None,
GridLinesStyle->Directive[
GrayLevel[0.5, 0.4]],
ImageSize->120]\), 1, 2]](https://www.wolframcloud.com/obj/resourcesystem/images/f83/f83b39a2-ac8f-4fae-8c4f-638534efd2b2/277781bf9cbf8ee7.png)
|
| Out[9]= |
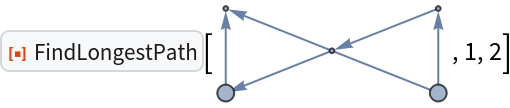
|
This work is licensed under a Creative Commons Attribution 4.0 International License