Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Try to find a proof of equivalence between lists in a given multiway system
ResourceFunction["FindListProof"][thm,axms] tries to find a proof of the list equivalence theorem thm using the multiway system axioms axms. |
| TimeConstraint | Infinity | how much time to allow |
Prove an elementary theorem regarding the equivalence of two lists in a simple multiway system:
| In[1]:= |
|
| Out[1]= |
|
Show the abstract proof network, with tooltips showing the intermediate expressions:
| In[2]:= |
|
| Out[2]= |
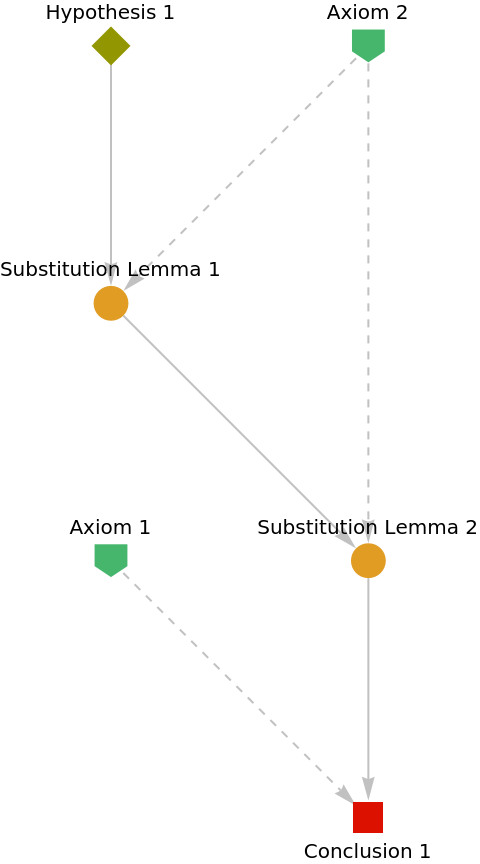
|
Show the complete list of proof steps as a Dataset object:
| In[3]:= |
|
| Out[3]= |
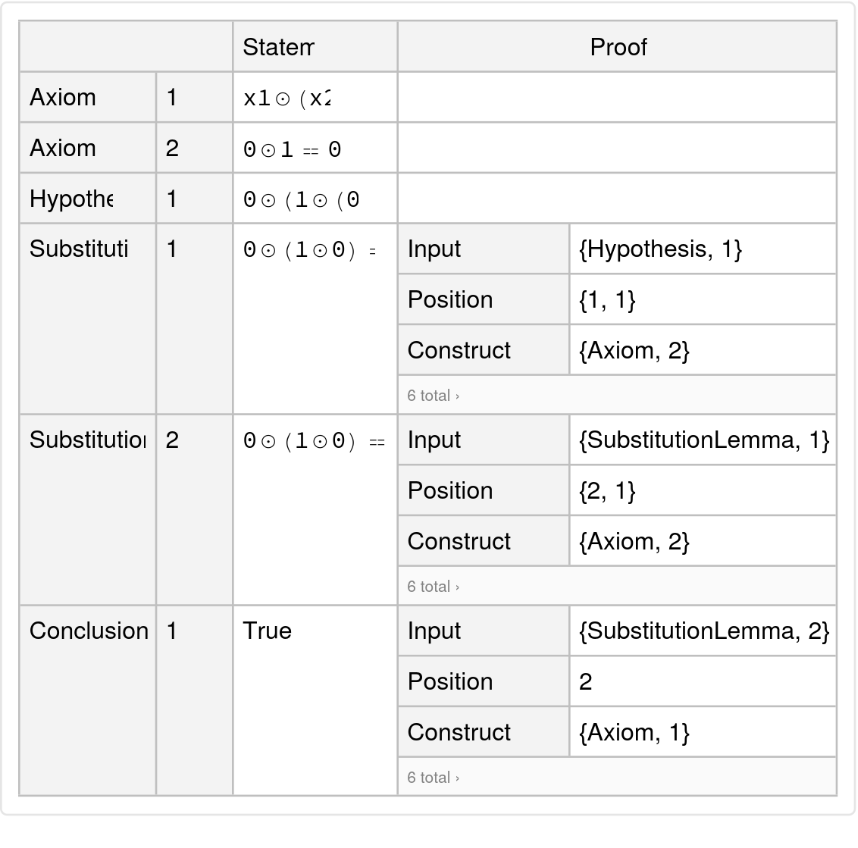
|
Typeset a natural language argument:
| In[4]:= |
|
| Out[4]= |
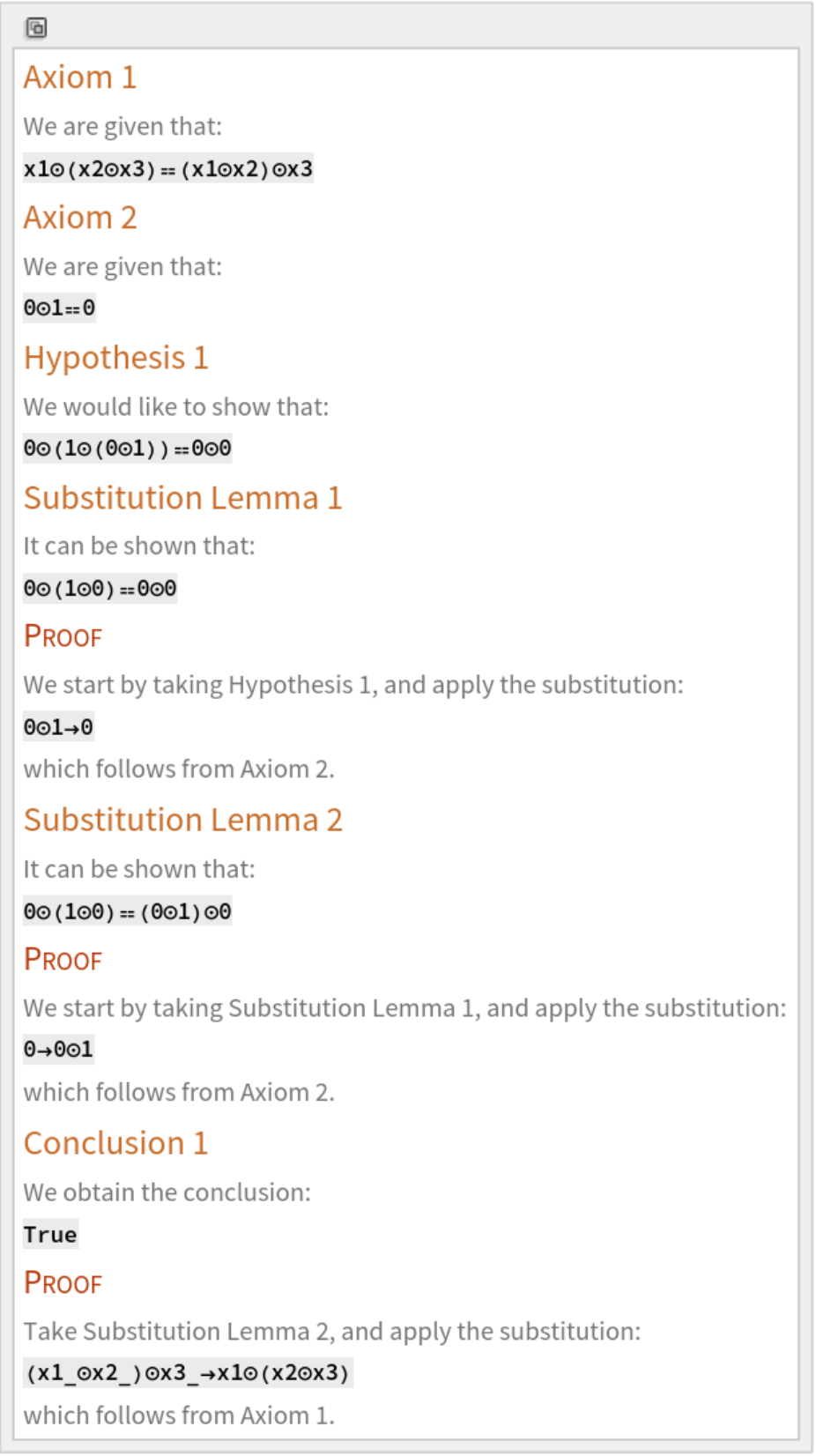
|
Prove a more sophisticated theorem involving multiple rules and hypotheses:
| In[5]:= |
|
| Out[5]= |
|
Show the abstract proof network:
| In[6]:= |
|
| Out[6]= |
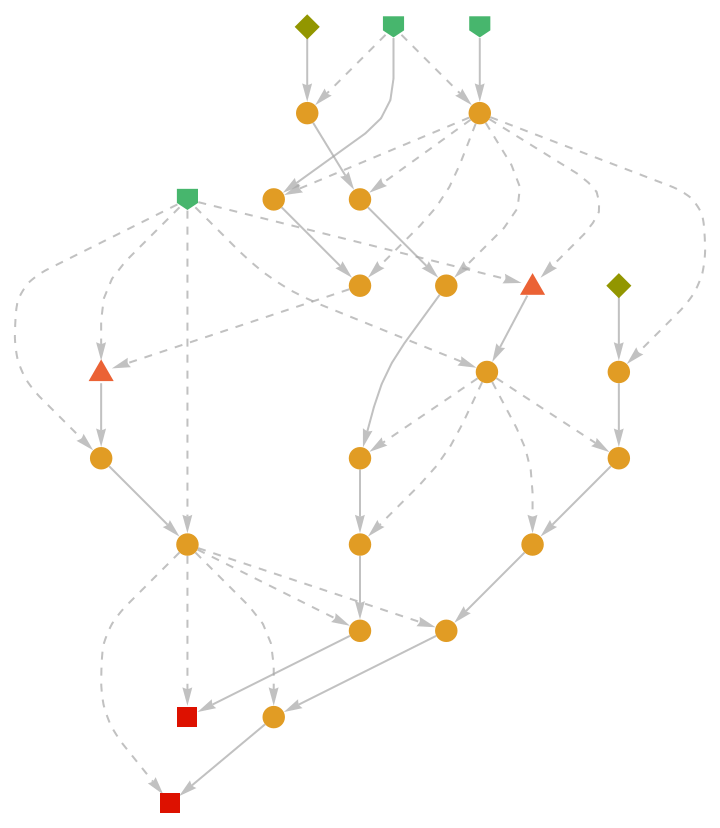
|
Show that a list equivalence proposition cannot be derived from a given set of multiway system axioms:
| In[7]:= |
|
| Out[7]= |
|
FindListProof accepts both individual axioms and lists of axioms:
| In[8]:= |
|
| Out[8]= |
|
| In[9]:= |
|
| Out[9]= |
|
Likewise for theorems:
| In[10]:= |
|
| Out[10]= |
|
Use TimeConstraint→t to limit the computation time to t seconds:
| In[11]:= |
|
| Out[11]= |
|
By default, FindListProof looks for a proof indefinitely:
| In[12]:= |
|
| Out[12]= |
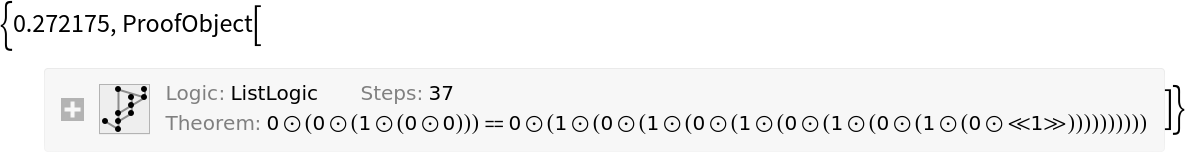
|
FindListProof will return a proof object for a particular theorem if and only if the associated path exists in the corresponding multiway system:
| In[13]:= |
|
| Out[13]= |
|
| In[14]:= |
|
| Out[14]= |
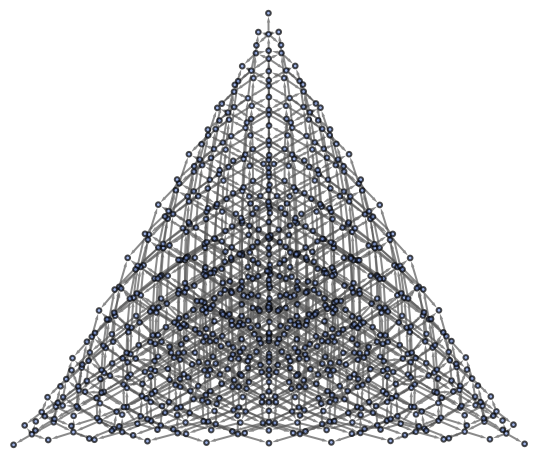
|
| In[15]:= |
|
| Out[15]= |

|
| In[16]:= |
|
| Out[16]= |
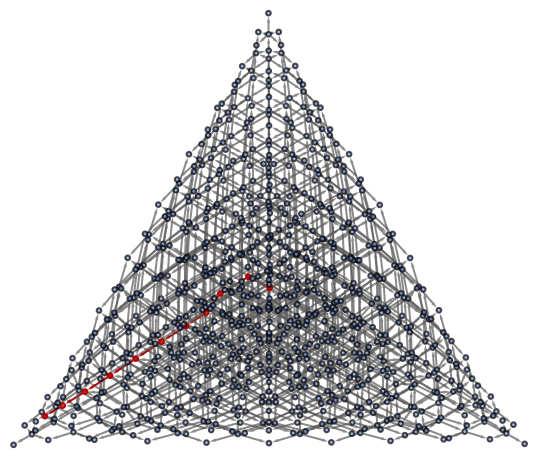
|
This work is licensed under a Creative Commons Attribution 4.0 International License