Function Repository Resource:

FindLinearRecurrenceEquations

Source Notebook

Find equations describing a linear recurrence corresponding to an input sequence

Contributed by: Max Piskunov and Jan Mangaldan

ResourceFunction["FindLinearRecurrenceEquations"][list,a[n],n]

attempts to find equations describing the minimal linear recurrence a[n] that generates list.

ResourceFunction["FindLinearRecurrenceEquations"][list,a[n],n,d]

attempts to find equations describing the linear recurrence a[n] of maximum order d that generates list.

ResourceFunction["FindLinearRecurrenceEquations"][list]

represents the equations in terms of formal symbols a and n.

Details and Options

ResourceFunction["FindLinearRecurrenceEquations"] gives the equation for the recurrence itself, and the equations for its initial conditions.

Examples

Basic Examples (2)

Find recurrence equations for the Fibonacci sequence:

In[1]:=

$ResourceFunction[ "FindLinearRecurrenceEquations"][{1, 1, 2, 3, 5, 8}, \[FormalA][\[FormalN]], \[FormalN]]$

Out[1]=

Use the default symbols for the recurrence equations:

In[2]:=

Out[2]=

A more complicated example:

In[3]:=

$ResourceFunction["FindLinearRecurrenceEquations"][ Table[Fibonacci[k] Fibonacci[k - 1]^2, {k, 10}], \[FormalA][\[FormalN]], \[FormalN]]$

Out[3]=

Scope (2)

Use symbolic data:

In[4]:=

$ResourceFunction[ "FindLinearRecurrenceEquations"][{a, b, a + b, a + 2 b, 2 a + 3 b}, \[FormalA], \[FormalN]]$

Out[4]=

Use the default formal symbols to represent the equations:

In[5]:=

Out[5]=

Use different symbols for the equations:

In[6]:=

Out[6]=

In[7]:=

Out[7]=

Applications (4)

Generate the convergents of a quadratic irrational:

In[8]:=

Out[8]=

Find the recurrence equations for the numerators and denominators:

In[9]:=

Out[9]=

In[10]:=

Out[10]=

Solve the two sets of recurrence equations:

In[11]:=

Out[11]=

In[12]:=

Out[12]=

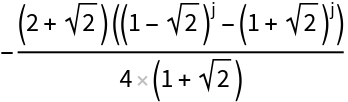
Verify that the limit at infinity of the ratio of the two solutions is the starting quadratic irrational:

In[13]:=

$Limit[nuFun/deFun, j -> \[Infinity]]$

Out[13]=

Properties and Relations (4)

Here are the first few values of the Padovan sequence:

In[14]:=

Generate the recurrence equation and initial conditions with FindLinearRecurrenceEquations:

In[15]:=

Out[15]=

Use RSolve to generate the explicit solution:

In[16]:=

$pfunRS = \[FormalA] /. First[RSolve[eqs, \[FormalA], \[FormalN]]]$

Out[16]=

In[17]:=

Out[17]=

Use DifferenceRoot to generate the implicit solution:

In[18]:=

$pfunDR = DifferenceRoot[ Function[{\[FormalA], \[FormalN]}, Evaluate[eqs]]]$

Out[18]=

In[19]:=

Out[19]=

Version History

1.0.0 – 14 April 2020

Related Resources

License Information

This work is licensed under a Creative Commons Attribution 4.0 International License