Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Find up to a specified number of isomorphisms between two permutation groups
ResourceFunction["FindGroupIsomorphism"][g1,g2] finds an isomorphism between permutation groups g1 and g2. | |
ResourceFunction["FindGroupIsomorphism"][g1,g2,n] finds up to n isomorphisms. | |
ResourceFunction["FindGroupIsomorphism"][g1,g2,n,form] finds up to n isomorphisms, each having head form. |
Find an isomorphism between two groups:
| In[1]:= | ![ResourceFunction["FindGroupIsomorphism"][
PermutationGroup[{Cycles[{{1, 2, 3}}], Cycles[{{1, 2, 3}, {5, 6}}], Cycles[{{5, 6}}], Cycles[{{2, 3}}]}], DihedralGroup[6]]](https://www.wolframcloud.com/obj/resourcesystem/images/044/04461ed0-411e-467a-9d8c-2f14b7737907/31ee35408a2007c7.png) |
| Out[1]= |
Find three isomorphisms between two Abelian groups:
| In[2]:= |
| Out[2]= |  |
Find all automorphisms of the symmetric group of degree four:
| In[3]:= |
| Out[3]= |  |
Test if two groups are isomorphic by seeing if there is at least one isomorphism between them:
| In[4]:= |
See that the following two groups are isomorphic:
| In[5]:= |
| Out[5]= |
See that the following two groups are not isomorphic:
| In[6]:= |
| Out[6]= |
Compute the automorphism group Aut(G) of a group G by finding all isomorphisms from that group to itself:
| In[7]:= |
Find the automorphism group of the following group:
| In[8]:= |
| Out[8]= |
Format the isomorphism as a permutation list:
| In[9]:= |
| Out[9]= |
Format the isomorphism as a disjoint cycle representation of its representative permutation list:
| In[10]:= |
| Out[10]= |
This is equivalent to wrapping the permutation list representation of the isomorphism with PermutationCycles:
| In[11]:= |
| Out[11]= |
Format the isomorphism as an association:
| In[12]:= |
| Out[12]= | 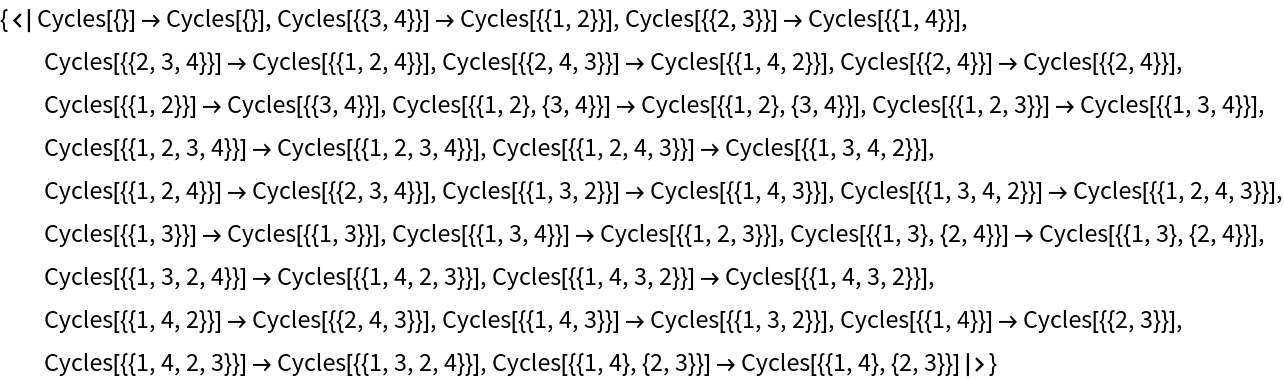 |
This is equivalent to creating an association by threading the domain group elements to the permutation of the range group elements provided by the isomorphism:
| In[13]:= |
| Out[13]= | 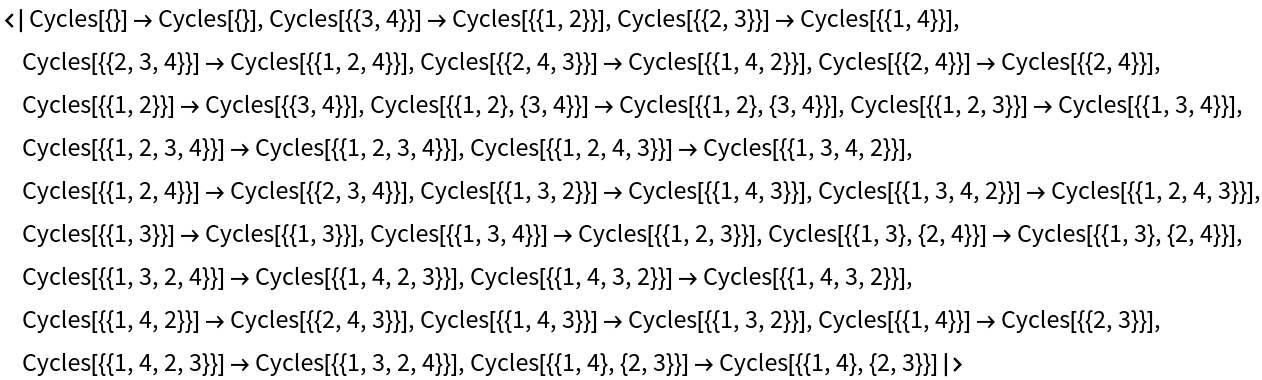 |
Wolfram Language 11.3 (March 2018) or above
This work is licensed under a Creative Commons Attribution 4.0 International License