Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Find the indices of approximate grid points
ResourceFunction["FindGridIndices"][pts,{i1→{j1,k1},i2→{j2,k2},i3→{j3,k3},…}] finds the grid indices of the points pts given the indices for the is. | |
ResourceFunction["FindGridIndices"][pts,{i1→{j1,k1},i2→{j2,k2},i3→{j3,k3},…},delta] finds the grid indices with a maximum deviation delta in the index. | |
ResourceFunction["FindGridIndices"][pts,{i1→{j1,k1},i2→{j2,k2},i3→{j3,k3},…},delta,max] finds the grid indices with a maximum index distance of max allowed to jump 'gaps'. |
Make a grid of points and figure out the grid-indices:
| In[1]:= | ![points = {{1.25, 1.25}, {1.25, 2.25}, {1.25, 3.25}, {2.25, 1.25}, {2.25, 2.25}, {2.25, 3.25}, {3.25, 1.25}, {3.25, 2.25}, {3.25, 3.25}};
known = {1 -> {0, 0}, 2 -> {0, 1}, 4 -> {2, 0}};
out = ResourceFunction["FindGridIndices"][points, known]](https://www.wolframcloud.com/obj/resourcesystem/images/de7/de7a41fb-b002-4038-8149-531348b94809/1bc63e881277c769.png) |
| Out[3]= |  |
For some given points, and known indices, find all the indices:
| In[4]:= | ![points = {{2.2457107617837337`, 3.151739383363539}, {
1.2194058590709853`, 4.177855965476845}, {0.18612053291149167`, 5.255740242248263}, {3.265717355719692, 4.302069883742035}, {
2.230859571348209, 5.330745256117548}, {1.3451808496165396`, 6.274072003786259}, {4.169600297056586, 5.34635094414414}, {
3.3000345340888666`, 6.1767441646481815`}, {2.21976647442846, 7.186465699338501}, {5.279614167307427, 6.223906792689673}, {
4.282957106416612, 7.196190176911716}, {3.2616964858975876`, 8.310921559418997}, {6.156158838009473, 7.2418246145486025`}, {
5.256388542385789, 8.258148926045028}, {4.216236774163855, 9.26524266508286}};
known = {1 -> {0, 0}, 2 -> {0, 1}, 7 -> {2, 0}};
out = ResourceFunction["FindGridIndices"][points, known]](https://www.wolframcloud.com/obj/resourcesystem/images/de7/de7a41fb-b002-4038-8149-531348b94809/1731569739c3fea5.png) |
| Out[5]= | 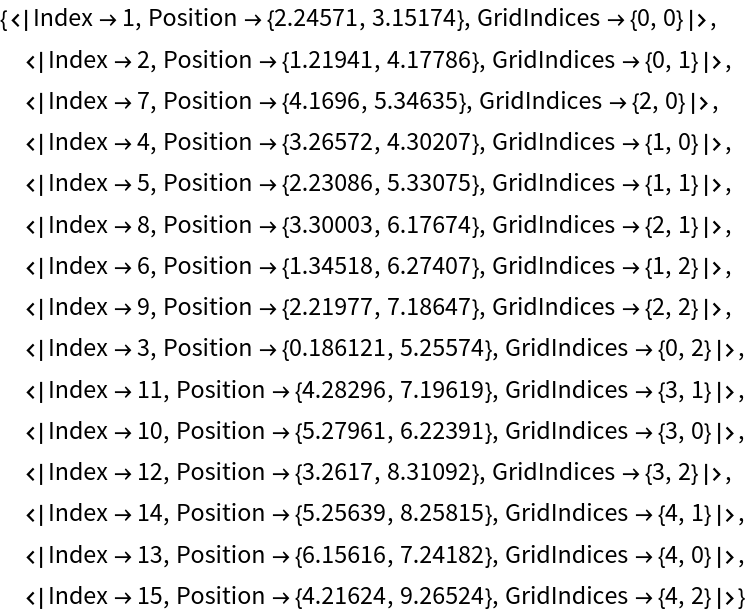 |
Given some point and known indices, visualize the configuration:
| In[6]:= | ![testpts = CompressedData["
1:eJw1WQdczfv7RySENEihhIjsrIzekj2Ln5u9cm9khIQG2rvOPqfTOquyZWeV
lU1U14iSVWSVjLq67v/5nE//59Wr5zzz83z283y+PVdv9ljbolmzZgPpH8MO
S5OufK/PRG6PiA/uThIUrnaOe/89G742l4NbrolEJ1ejnuGflXCuSt12f3sy
yKTZg2HperzSPESPoczWY1VZOOzGzxtz/nM2vNgPeQz+R2AxicubHQ7BY63v
+Lar0uDYUCBaYRmCLwqrJ2Pl2RiXZfgjcXskHi53DWyTno2RLo4ehs5hqFrj
O8HwbRaWx5RK95G94HKDZapLk79pYTBkIM5GaAiBRTROZB1y8EnWwHXFgy7f
tiRjSU6rJTk3BCjqG1zU96wcH6/N+XgtPhUtBj5oMbBbCLa2Gno29J2OY08B
kiyMen0amw1d9wEmUyrD8dGdRuaYBmx4cmeEIjbtScyy1zr081/d1z9WjAJy
N+etDkStzs4TYcCM173MJmXC/sHY7QODxQhs86nPyV+ZaEtIXi+Br+evyFNb
BAiYIchumRCCqFObPX8hEz4vcn60ny4BE29WZaJocpdlfmMlmP/mxKYhmkx0
myUsPLdZjGenNz5bOFILUe/pIp0sFNPph4dLJs5sfHZ6oLkUfYjhkJ4JEvdu
YyiFXcgZG1N/ASo+RbUsXxyGXz2JkZsC8yrnKVvsQiAebO3UEKHDshv97m+/
LUKr8t3TKtwycehbyZUZx0QYQuLjC7LwdW2Y/Qo3Od5ezV0hj9Jhqsr74OV/
hRixMxEP3+vwckyLyUt6CaFMJpiSCfHtqC35b4T4vC78bXpeCs5ld5IFbkzG
PkJWfXTImOL5ed1jEUyJXLVXh96OP52uDJGiF8NVOj6/tUJUpk/x3DQ+E1e2
zu3lWCHFNkI/lZncr1KGTk6pJcHmWniP3v/r65swVOeNO23XTYc/Wrbvu32z
AjcX0o/BOpwbnHTY6EccOk+8Or0srEkuF/N2Xum43UIJQiPF5wbTftDjOBny
ie09Pwv1b49ZTGyv0I977ygRPPzz3f3T5Jhs+9jNNl0DwwF+hgNKxRjH4LIW
91dG3F+5R4LqgqDqgrGZcDj/ot/5/TIws/xvmYjFkRh0U6Ax4fivhIZMbn9F
im5rf1qvXZjF9QJluHeXYKwGO3cQnJGgE4F7My3n3xGDsUet1KK8rKxsWbyE
92e1Fm4M8sX4k8EVrd6u03Ex519r0n8jQkx0dLTRc51eLgyXcz3PLD6PJ6So
8vn+0SRNg4WFHUKs90sQfDi9e4vfGhw3nhERs06KCzZj7j1urkX8oHPvNP+K
8OjEpIrrvXRQL1DsdNGJURJEBnt03O5fKdYaPXpYaaPDl/lLh7V0kcKloM+k
nDgdUn46DOq6UoB1dRMK+pTrMCtyZfeNn6Wwn5STOLJCh43l2bledlLo7v0y
l8szud5ABfeXkonLzqUX5j6UIiDjlajnkSwYM8ZlBWJnkqOcLIh7ek5N+SWH
TVjd0NFKDV4GGd+/8UqOkCwT77apGvxjmZp0eYcUbzvP3VS7TAvr9znCDg4y
Lg/V4cfuRV/kayQgq4qgGB3KXt0amD5IiMa1F1c8KtXhbkD+oZ+zFUjbdn9M
1SgN6NQ0cb2kQNCXiz+Xr9AiU+Ixw2GxFHk/ywO/3NDiuuWa+KGThfx87anD
o8U+h09tkeDwKfo1JhNHGJ6gwLOG3esvPFajJvv6zFFrZKj6tb+26B8Nynob
hkjXJXP+Bi2ufO+3NCkvAW8f2D1ryNeixYCozk9nSXFHPfl0XQ8dNIT+bSvD
PlKP6a8DO856+Ahgw36MysRwBq2SEewyYvk550yorAaX9faTo9hpdrHTIzVs
jUJtjVoo0JPhp2rMZoKvYnwbV1g37j8NbmzpdmOLUoLE16MTXy/Rcn6SAneO
O9457qXlfFuR/nyaXqZDQHrVrvSztL++/Mr7coz2V/CLn8HD5bA1MWrZIkeF
wwsP/r2+UIAHVXUNQdT/fcXv/ZzFUqjn9TNvW6qGpbFh2GU7MW6+rt05bqIG
QxhDK0DanOzi94E6MPHK5QpcX33M0/GpDjFudsJpnZNx5tkn//M/MjEy5d6f
J+bL9fulop7fZxWb+Hmws6Naj41qFHqc2onTD9rx/dXbgtNDrgr02G9bk34F
11ds5/TO/7i/WWWcrt8r1GOT0Rp+f37l7Q9pogV2nLYdx+lpldz+WnKT/lHu
3y27Sb8qges1ctqyFbc/9P/0KJkeL12q1WPfK1yes4bT3jUi7t+b056hvD8m
Fzi9cg9vr+VtTsOfy9/Z8/M514jbrwzg9AP7ZAhHvWm/yyEdJRbbJy8LFOvv
//9NU4G4k8rtJbD81ip4ookankzhqBTnNUf2DaDxstt80/rrAwnyVYPftdul
5vqxQoTlEeOJGjOWFMlOXpWgsfmeSzbjNSCpYFRnMUx3XOu+hfbzgkeSEWvN
5CBpTWu1BnHnyPEYEew3Tl9SpNVwvwoBfu91qeiYnImKjvUGv1fLYT72mNnY
uFQ0XurYeEkqxn7pYvpLw6Y3Uza9aSmDukuAuku/dL4/5kr4ufgrHRWtd1e0
thLApcbApeawCsvfRSx/N1UM5u4YrR+9/V4ZljCHpmoYkfpuZzHKbiY8v2lG
+5nMDNaJ+PlsTv0l9SkyIb65Dv7mSuvJhAVkokC3s0Lrs8/UnO8uQqhNfYhN
uRorWHuHBVxuqOX+EgRgpJD2n8eAUx4DFiXzeC9qMYnMB1fKeP/ymmgrGRKf
U0AFWjiS+ilzEaetdHjQ7uKDdqOSwdS+ddfhALN71NSfIB0oivoQsRwPmV6i
DpY0TAE9k3CZhrFjXSZEFIb1awVYtyvmZenXR7MiBcLyY808ggTIO7VKeb53
BG6diH9nMFOFnn0Kh2meCvA5lBQOqnC9jcMu2X8K6N4smvJtqxrOPx5FroMc
1lln2/3+W40FN8pLhxQqkCoQ/dWVzqenS0gyVI7jZ0bO2jaBr/9mU0Tcfwad
73urnyxpI8Z7gwNrNms0CCHS2luIO9ETVM6ZGvh1afxfanwS4sw8vjoaabn/
XUlg6B7lE/4fD7cv1sgRIRl3JzpYh0Cfq047bsjgtXmjolKayek6BSbUV4R1
pPWkx+sluG2fsuE4raegmsutbaLFsGE/rmeAbsu4Qaub9sdUFUyYgUky3hPb
mdaPNo4uVBsF1/dTg6mf2yLjfneo4feQEsTBYhw8QPBLw/0VyXGltU2QL91f
TG3Cdxm8r2S02VOhBEP2/UIw9+DYw59jU3Gi9d0eQzoJcelj8xOtabyXCrZM
vD5YgRfdgrd9o/3Z8s+OivHldB99PnmumPZjz9eh8e1yBRjHGLTfApnhZBkm
O1ocW0Dt0/9rHhk0v/Hthg0y0KLUgBwMEGHQzVzb1+1off5FEQyI5/L2Wsxi
htGxgNnvWfV/ajFS8njecnchj2sTjf81j04zu8bj6tHrbgE0fo8U0zouWCpB
+RVi/EjHp867R9gnyhG5IiHm27UMqLb6t8un+qULsYumqJBvZfY+JF0GVo5E
OGt4XRIhRTsmaKnF9I4L7m9aJkQAM/TVwvl8xIqE7bF83ZzXcvtpyRjD+Pe0
8GeG+xMwTNhjX2phk36reBQZSE8s6afjemOEaElkvaMOH1l8I5NQUnPGYUqV
Eh32pKwueSSC92D1xXA6T8J/mJbOpHxmDVOg8dfv0ySZPi8rO6TCqIJ9Lzd3
lWBE48ZY9yMq+L1tfst5uwiGrKCh9WH1e2TBvrlyZFuSRhc1v1+dEnHu616v
NFovzL23WopFVbcNRPs0YOniXcRzP221WMrqoocJyGOB0HnPwqs5JsdABhTv
SQKnI2KcYvhcChYz2CHhNK3vnQyo3rl29erVSTQ/zOzwsSaa5oeJ64ckoyOD
n+mYNZPAQqq3P0l0bQ3BRAmKi4qKPOqb9BUiREdFRd04oOLtL5dzfRofGYM8
Kc+vd6rx6uXLl6uWiXi8L9Tc/+kkvbyxgt+3zYwTMf2hyZ7nS9Ng9zt3+65W
Qo4b0jGhb/EfbQqEeOq470fqlQx0HO3hdO2pFGHrC299o/XzeUxy3oxNcpQ3
nxobSfvTrXHLh69Uv4X0mjypkebDmcSWaiE2LSONLVrYnhn0ZW9hNPd3Rwv7
+Huh62cmYaBXz3aLaPyqZ28OKFaLYeaivVZI43XOf+WR7ofovBJEOHr1TUek
IylSPdFu0U3XzhQPIxfNUYCRx+m8KP+WNepigggOtcNnNN7O4PwOAjAkmKFC
D4VP68pDQjBU+lKNxnhTF61XPFKZIdU/elqSgE4FK94Yv1Vi1trAx837CmG+
RzjcsVIJf4yqfE/13Mo3xu0GnUnBEfuesfklobDqvLT/s4spOL2j+4ME2t9u
tV3GXKX6+UKHd9dZfjc++KQynOabkcGUb/nu3/DFmeL/ecTg3NBgOQzlt38c
Oa7Ck+ZliuyUeAT84z2izV41IluRwC4G7o2T7+cc1MDjafl21EVzuxwNlOH9
ftvVhWE+45tqMceVIk2KgLpDtaqDhRKbWCF8nuqLid1LJtL4Oua9GpBH9av+
nqbx1ddHVE9un9d6+zzKR4IK/ggqQDKnKd6c+tij9edkqLVYUWtB89uZ0AoX
hd7fZcpX9H4WiMHYtew+IvM/Pki4/hgNKIpq1QIZPJljtya6nvYThbF6mxbh
zvvCnPtFYWrwX9q8EckoulBv1uZXKN7tLevh80GJyoKMaaMpn7N7KaksOJuC
EYN/u12xFnJM+6t6rPX3NDMZPF483feF+lPew6er824Fdo4kyeB03I9zEfpG
xiCe0Axo0PHJp2OybUIM97u0KclVA8foWxbXVElYtc32YdvzMuzY3/f1mU5i
9F5MnFsyVN+q/+ThwPO7ZjQu8+de3yz/LMLXZ5np8ROTMWt81/xl6RJMHrCh
Q29TJUgaMKytCBqLka1Naf3kLyMPswXInUmKFL/ef50QXZmA7hc/ajaliuef
zei808u/S7lfop90m3byyiYFzpeIa5/9m462KQYxC0visZwF1iwDpodzxgj8
YjhN62nwd69G/9ZSMLR/lgr6QBYn4jZ1Y+4BDQTeEfdCFLE8ng5axC6kFiqi
eb/WU336YtB3r5VJPD8bk4zlrU7ouhkn8fzPTIm8tn9OH/NKxO9dcyVaCF8u
byWUYBm7aGk+XIof1Z+vEsKhtVtkINF6O6pfR/7e1ENN+4G9//S9HQqZxMDu
6pI0LPboEG3snoz1Po1l4+j8yTpcu6PuUCJ/L6L1l/4kJu1JlRRHiG1E+eTC
ITNvN/8iwABFn7d7qb+RgRZ3RbbJYGGa3MkAc3txUyJ/v7qbwfGVeLSjsG1p
/TJz4R0p9k2gQKl+smSB1yXxeDqreX9eJOF78unrLyzVKKHu7IqOx+svlZ0O
BKlRPXxjQr5NItyDKdJXaly7SANyMRasuxZv1WDlfZxpjL7OGzopWX/frPGX
Ygz96NBZCZaGVHtL9fLa3BS8oetopxuvF/aeT9HL+8/m+nOof3o/h2SgqrFb
1XSVHt/Yy+uJipmcbt1SwN8PA9UYzdq5k6TPd2IfavX+c71iMcl581DdRRlm
+G/UeH0SY1rVwEi/cclgz0RO44TwZA9FtL7LV5Pkppjfs12UaHy594YNZGDP
TVu7KjEo0q98dbWc671RovRUjGhZVSJfv9VKnB/pftxnqIy/WxGdt+BB9czW
csyfeHCwBe1Pu7QzlkWPZWiR5NKthmiHp+TgGeWX4xNyni9Lgz0LcFoc2jBG
fzqPrFadzS4UYo7kY6nbjQweb64Qh5ljWt83bTrsbDwcj7Jiozvj6fx0YufR
1EReL3RVw+O4j1mfF7GYfOvIbMlkDRau6O/93T2exzNTg1zLol1xhyPQhwU+
S4NSN1JsFs7f2+ZosDh4v+rv+aF4enztHdn4ZPhV3U8bayFCt9G+FZfo/o+3
HLr6WrgEjL2D1nd97esbSUvi4LK7sb6W1iszGxiWCFvGuJWBffPUrhFvBAj8
Xv33QSs10sfu+Px8aAz6zlY6rQtWo5QZbI/n47mH6jmx/Wzl3VhcDCCDcDW3
Xx8Kpl40RYPV16I79ToQi5+GkpgBU6kOya54a/6PHDlP3eMENF/xgvw/p+Yr
+DvDeyV+K7ufMlpC66sVadJ6a01mZT1l+KE+NsHpQgrXvyPn+TbtX+a2LD8R
+yffXHEiIRWpofL5NSuTwZq5QPMTMmxLZmCDAKstI1dZ0nnE2Kn2cShbGRv0
aJAEi0cp7DIsJPBmDKkcWTf/Klv5UoxbhGKNKN82bzhkPSgEGdvDHL46pkNU
eO6y+ft4kNX2sGHpUDH+sVAIiS9xp/lmdomhmPDBcL5XlZrLz0aAPftenqaB
P5GLmsfgwHvFzPCXUgxZUDxU3kMMaUHXTz28FWgZud650laEfVlrBnXyU2Bb
TI3Oth3VD6fz2luOpjow8azbzoUJmH1jqd24scl497/Of51cJcCGYOshCzop
QVTgE08BfJwrTV/S/ljIGJ3lvB1a75NGdN8WUyqHyOXo8dF03sf7d1zyoigR
HoLGXVIaz7ZMYJwAFoZpYQaOj9aWXTWNQzaFk16UAebGyCAScqO5bUUnaX8z
x5NiwNhzQ9S8X9uicM5tp4fgsAbjHKb9vjAlCt/6xw0vNdGiB+vHyCiwzwaO
GxXo4FeK7IMSjG/7WOtL59GXzwRzZFhza7Cs0USJEkPnjaqhQpwKmWP9jub/
VYD5kak/ZXz+2X7M9/wa1xCP1qRWbJ/OzwW6F9cbpI18UJwBnS95nhuOLayB
Eyq86TJz97GaWP49oIcau48Rxz8UyTNm9ckyp3P3Q/H3975yzHuc/aF4hQKd
W8WFTj4ch4VjD6b9TfNh980kwOiFAp0CjMaH0/nokdPP09w2AazsmWQlReRX
q9sf6Lyvs7rt0+9PBdyXT9qVMFnIadIPaP92hGR6JCbtav/2FI33BWZwXg4i
R5jT/tTLx0fiIvFnLE/j+0wSA8Z+PCAdlYTmyRKxod9R9bgHGdAwB14x3P/D
DHxl+HgUmPq80yrkqEmhMkJv36VSrbe74BWFKKZYreb12qpQfZyzZ2i4/z+i
9P0xOKrR98cnNQJZmQRdpPo8v2iaAvfvESRRnbqhy5UNVO+JhARyOfbP/71v
fq4EnX0uWfisV6D/nhKHPf+I+L3gQ3llgZVvQYkYY98mOb/d2OQnTIqed/17
3vVVII/BUhkihzyLGDI5GTlHCfo07fd2SvRj8DEUIytiR1RQPWzOwDMSzF0S
3c+fXRWfXAcJsMjgiKfByjTM0vycpTkfihZ/HGr+x6B0+LOGRtN6bnTPbqT1
URRo/zBQGQpv04t/mc5R4bbN9ts2zePAyItEb2LgEcPbPaWCgJpxFkahzuzV
oUZjKV4MHZGz45UEJ78S47YMqdIMk7/+U8Ag8EbJpbZKsM9h+7tGYyX7QNZR
iZsll8qHNiQi2erJ2CyKL/oEGfrR+ly42zV1noq/B3yLQEMb4lir4bWeLEOj
oHDcc+urgwTXDk67EDtSjOfqc90PJMvRstRJNVsoxdUJgz6+9lKAPUObbBAg
fuh1yzVbFVg++dX/ejvJ4cAerun8fd8mMb3ivgKbo6r999H46fUqQnH5oVm3
8VQvsGbkgnCMau9dvJfW64Fn1NDpGO5/COU3vcnjunDcORN058wOEc9f2kkx
6MXXgS8MpMgldtAcfv83o/2kl8tlCGYG+TLkvV2S97ZAgqXsxxUZ2hfZti9S
SeHbINvcIJBz3F/E87AMOZd3VcBKN9FKR/GwdCvGJw7rBIbrBLR/nKaFOU37
FIW5rCE6DxgZVh7F9em8Z2nax0s0XwMpwBYZ3K9ppD6eme/U3F/7cEzMtf7V
YzjF5X1JtLxGgt5bQ31HNZPCKkcnd5ELkCl32aheo0BNpzETc22SIDQLP3/s
pRI6xk8Lx5oXvbaGvqL8aeeRRd3bRqM+OtX2+Yo0TLDra7RjcCTqsgc6raR8
v9TVQPbtfhRql55wjp+rgmQ/GaijYLm2f7rPGRWM23sW3RkejvhhFoUjQtVg
4fy+GQED9/c3093F+GHsltmrpwSZvQINNW2luPtl/RYzIwlC9/l5Fb6RQjSe
NP8RY2j+wYLZNVI8emV/98toBbePkXP7HQmo+JsEr5VI/Ng1esaeOLQndiDl
S3r7IQkoFtKPbmr07/50uMnfEZwOUyO8YdnATVbhuPvCp9cjsRyOv7p5mBmK
UV8avf39EgUEypUXpLsiEVXS8vXhDkqc9DUMFyXFYcZn84GptL7M488cL/w3
itvT/B0v7Dnisi4GTraS5w50f/Y7O/+kr2s4Tnf6ULSmuxqVX051+mAfrl9P
qig5z5/y4vg5HyfXv4fMGpakp7vSec3wopoY/p69SqHPsyq9EvR1oHgUf0d9
msbtGyg+fR7mmqCvM43fcLryeoyejqfzWO83NFzPzzLI0LdftzSc15UtOb1N
F6qni2n+9Os+JBSJU+taW7+X4vT9vOj1R6X4ZXdg+48zMszZHFCcslSI8ARS
SKC6OmhrrrG/AIMMJoxZaqyE056cWu/Vkajx89ntOVqCb1ft1lZky8A+o6dX
Srn/Egl+snehozLc7xgnCSmM43KVHMQdrP6iAFnrjEcmg6FxL2OQvulexzja
v0caVgmH2Ubi7Oedx/osFGNWzcbfbf+VQBs9qe+nAhl0DLvL8dQ0KCU/lfZj
3R+Kv13lYKifUzLOMbve0fg0o+SIm4kU7DOacR7VC3vXGSvQVGcNT8aDrb8d
q5pL9e+g57YKYcfgpAyh4/rcnL9XgPsZbxsXkT+mVrgpkuvReZmXWPJh2v5w
pK0IvLl2EeX5zvk/BE+lKCppOBXlLEFciGm59145hs67Yj17vAR3Y4nhqUCf
Cw9LGj5IsXURSaJkMCv3rm7MleHEalX4qJEiSGqmzK+6KkNi1v2j43dS3dxY
OmlQihzCO+RgvQyn/vzl9j1AhI0Z+3o4vZNi3oKOVrtGSHCpYN29H1SPiXb8
7pz9WIpqz9u9nyxK4vmqoRTPT298drq/mOeXZVJ9XdPfW4h3u9KrGsqlXM9V
pL+//v4qBVGFdR2TMZ79oPlmn6Gnl8Rg3dWqpDH9JNg60LRkweKm8y9HBteT
L+tuRCfAmsEyMeYwOC3D508EK8Q4woDOzQ0MSqX8HS1OgHUMaB76Mzgdjs12
52M+KoQQlrn5m/2UgpH2SxXwHppW4DcsGmd7fY4eu1vEv79ca6r3j8vAPrf8
45aEjd3/ufdolRinO/z75wfKU21HSiNTP0nxe87CO9ar5PrvxnaR/LtUs/9i
sDFo+En/tWKcqL33oJTyuh0PNkwY6JCO1f1v9wzMFOFsgg8yKZ/Zf37/rSe9
BOjsFBXbis4DRW31t7WjBfg/DcYA2A==
"];
known = {556 -> {0, 0}, 557 -> {-2, 0}, 555 -> {0, 3}};
ListPlot[{testpts, {testpts[[known[[1, 1]]]]}, {testpts[[
known[[2, 1]]]]}, {testpts[[known[[3, 1]]]]}}, PlotStyle -> {Black, Red, Green, Cyan}, PlotRange -> All]](https://www.wolframcloud.com/obj/resourcesystem/images/de7/de7a41fb-b002-4038-8149-531348b94809/2897bff81ed2a398.png) |
| Out[7]= | 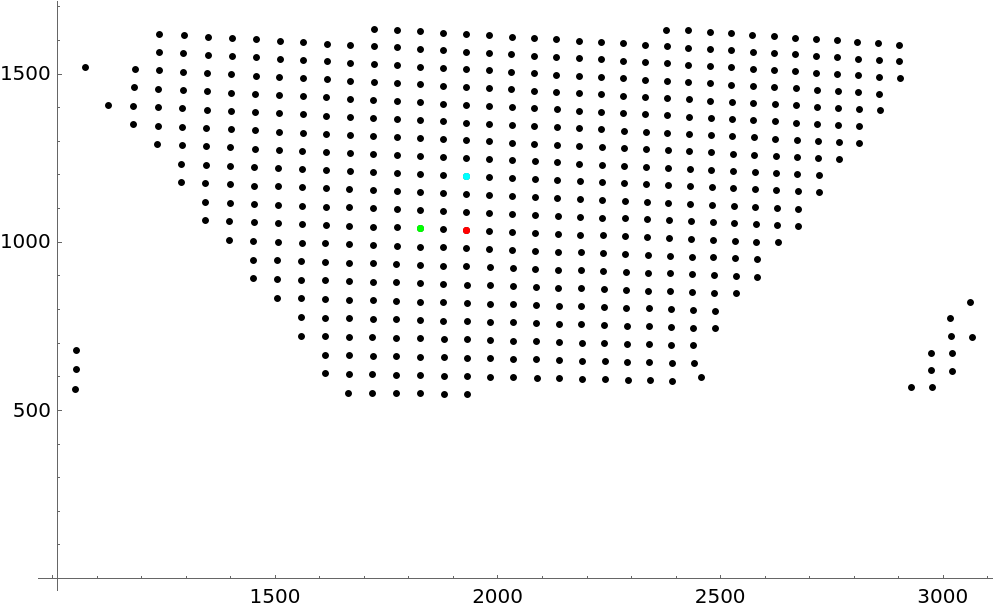 |
Find the indices and annotate the points with their coordinates shown on top. Note that the maximum distance is used to remove very remote points (i.e. it can't jump big gaps):
| In[8]:= | ![result = ResourceFunction["FindGridIndices"][testpts, known, Automatic, 3];
Graphics[{Map[{Text[
Style[#["GridIndices"], 6], #["Position"] + {0, 20}], Point[#["Position"]]} &, result]}, ImageSize -> 800]](https://www.wolframcloud.com/obj/resourcesystem/images/de7/de7a41fb-b002-4038-8149-531348b94809/3ebc1e1a56938dc3.png) |
| Out[9]= | 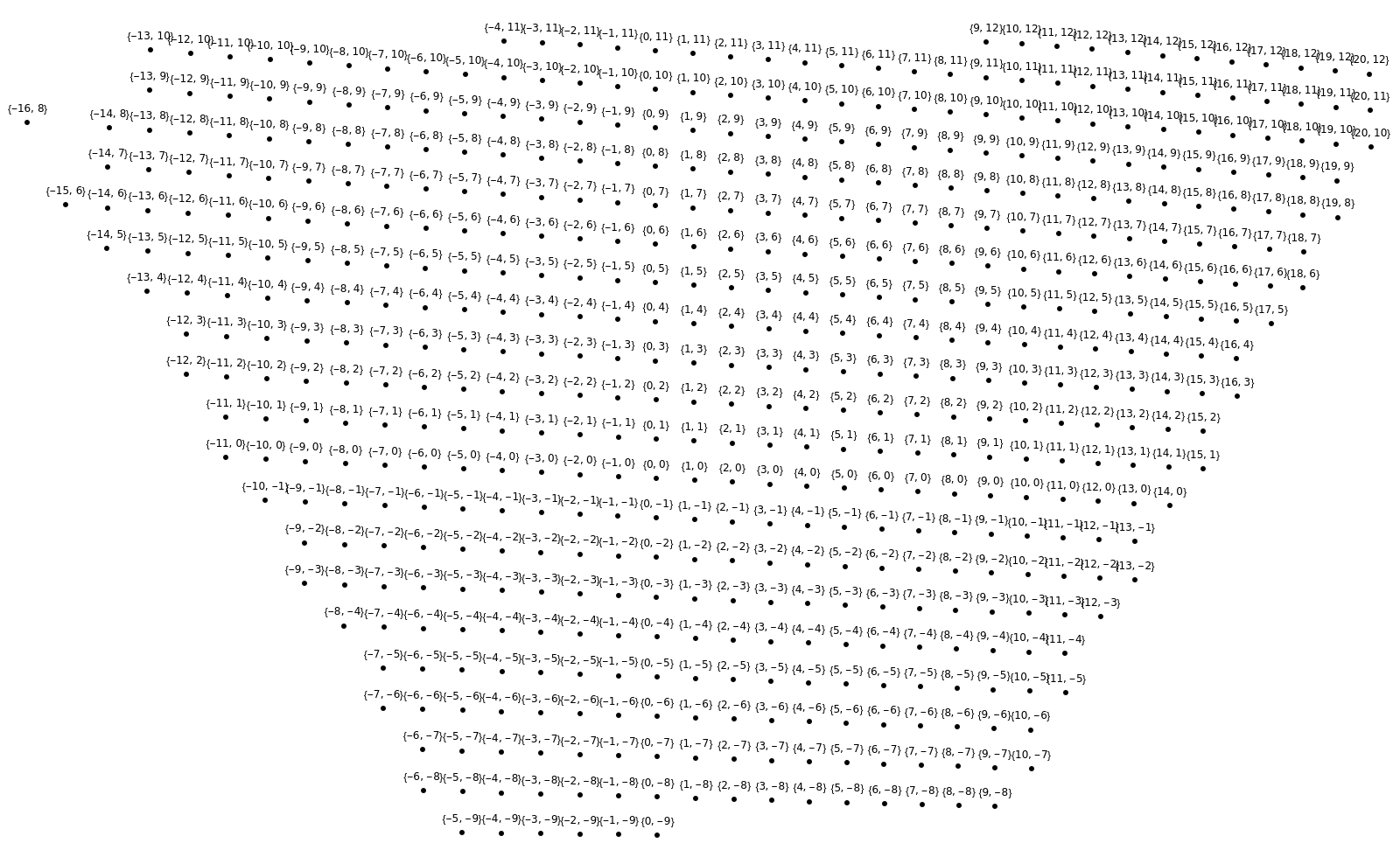 |
Create data points in an arc and randomly remove some datapoints:
| In[10]:= | ![SeedRandom[1337];
pts = Catenate@
Table[AngleVector[{r, \[Theta] Degree}] + RandomReal[0.03 {-1, 1}, 2], {r, 10, 20, 0.5}, {\[Theta], -120, -10, 2.5}];
b = {1, 2, 46};
pts = Delete[pts, List /@ RandomSample[Range[47, Length[pts]], 200]];
ListPlot[{pts, pts[[b]]}, AspectRatio -> Automatic]
b = Rule @@@ Transpose[{b, {{0, 0}, {1, 0}, {0, 1}}}];](https://www.wolframcloud.com/obj/resourcesystem/images/de7/de7a41fb-b002-4038-8149-531348b94809/20c45f8081b0ff2b.png) |
| Out[11]= | 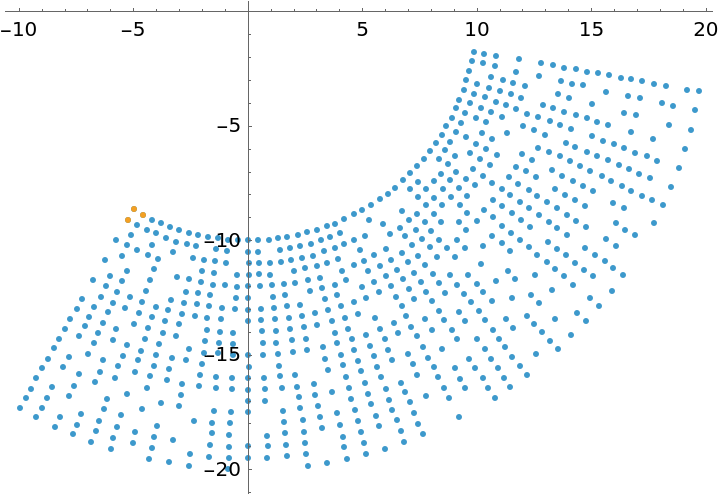 |
Find the indices with a very small delta and visualize the indices with the color indicating the order:
| In[12]:= | ![result = ResourceFunction["FindGridIndices"][pts, b];
Graphics[{MapIndexed[{Blend[{Red, Blue}, #2[[1]]/Length[result]], Text[Style[#1["GridIndices"], 6], #1["Position"] + {0, 0.2}], Point[#1["Position"]]} &, result]}, ImageSize -> 800]](https://www.wolframcloud.com/obj/resourcesystem/images/de7/de7a41fb-b002-4038-8149-531348b94809/18547c4968ae1454.png) |
| Out[13]= | 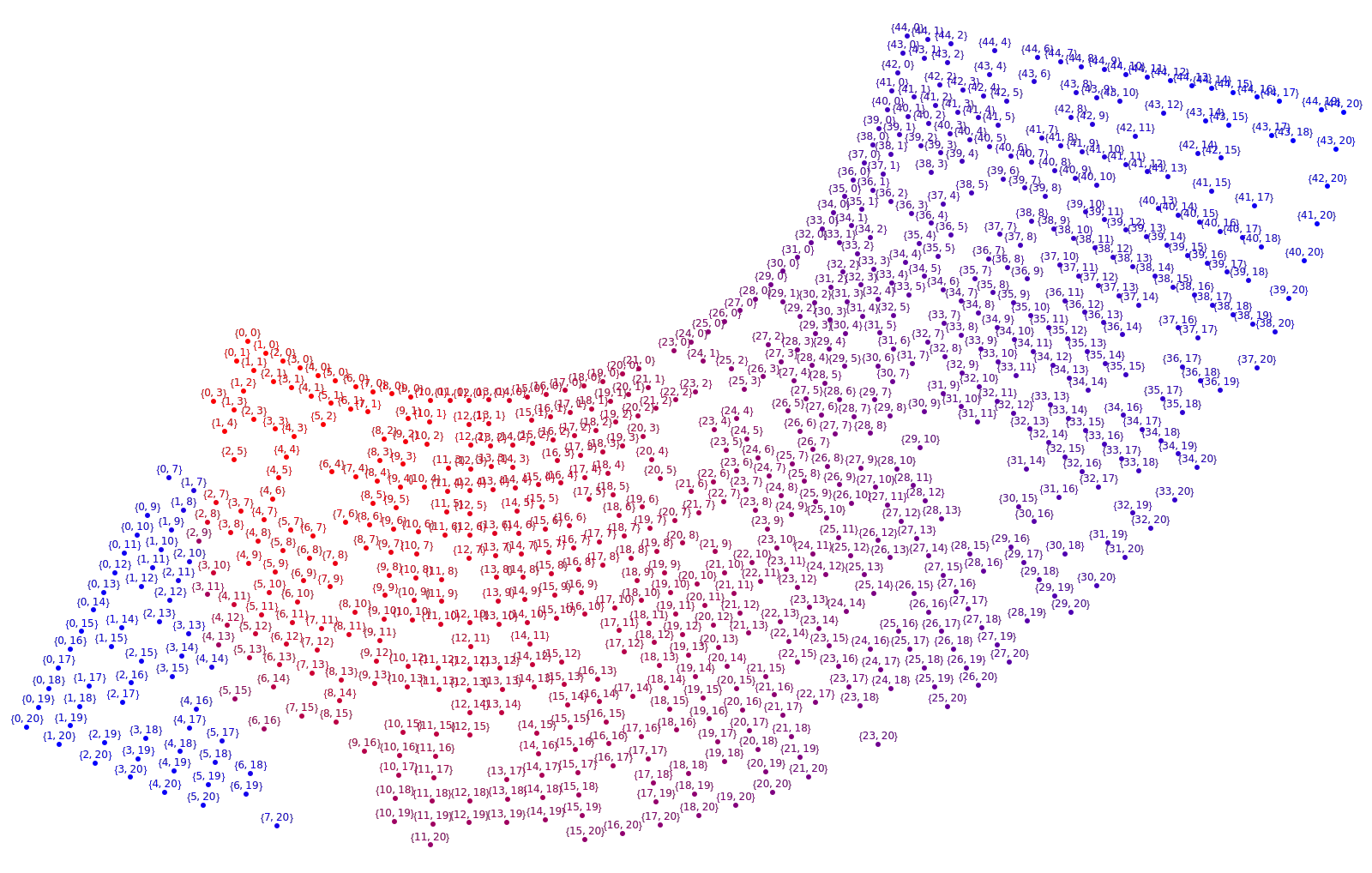 |
Sometimes the delta has to be increased to capture all points:
| In[14]:= | ![SeedRandom[1337];
pts = Catenate@
Table[AngleVector[{r, \[Theta] Degree}] + {0.2 r, 0.09 \[Theta]}, {r, 10, 20, 0.5}, {\[Theta], 45, 135, 2.5}];
pts += RandomReal[0.04 {-1, 1}, Dimensions[pts]];
b = {1, 2, 38};
b = Rule @@@ Transpose[{b, {{0, 0}, {1, 0}, {0, 1}}}];
result = ResourceFunction["FindGridIndices"][pts, b];
Graphics[{Map[{Text[
Style[#["GridIndices"], 6], #["Position"] + {0, 0.2}], Point[#["Position"]]} &, result]}, ImageSize -> 800]](https://www.wolframcloud.com/obj/resourcesystem/images/de7/de7a41fb-b002-4038-8149-531348b94809/1983d67fec386298.png) |
| Out[20]= |  |
Increasing the maximum delta gives all the points:
| In[21]:= | ![result = ResourceFunction["FindGridIndices"][pts, b, 0.5];
Graphics[{Map[{Text[
Style[#["GridIndices"], 6], #["Position"] + {0, 0.2}], Point[#["Position"]]} &, result]}, ImageSize -> 800]](https://www.wolframcloud.com/obj/resourcesystem/images/de7/de7a41fb-b002-4038-8149-531348b94809/0433274a612ff80d.png) |
| Out[22]= |  |
With a very large delta one can get bizarre results with duplicate indices:
| In[23]:= | ![SeedRandom[1337];
pts = Catenate@
Table[AngleVector[{r, \[Theta] Degree}], {r, 10, 20, 0.5}, {\[Theta], 45, 135, 2.5}];
pts += RandomReal[0.07 {-1, 1}, Dimensions[pts]];
b = {1, 2, 38};
b = Rule @@@ Transpose[{b, {{0, 0}, {1, 0}, {0, 1}}}];
result = ResourceFunction["FindGridIndices"][pts, b, 0.8, 3];
Graphics[{Map[{Text[
Style[#["GridIndices"], 6], #["Position"] + {0, 0.2}], Point[#["Position"]]} &, result]}, ImageSize -> 800]](https://www.wolframcloud.com/obj/resourcesystem/images/de7/de7a41fb-b002-4038-8149-531348b94809/79bcdcc29e0ccbe1.png) |
| Out[29]= | 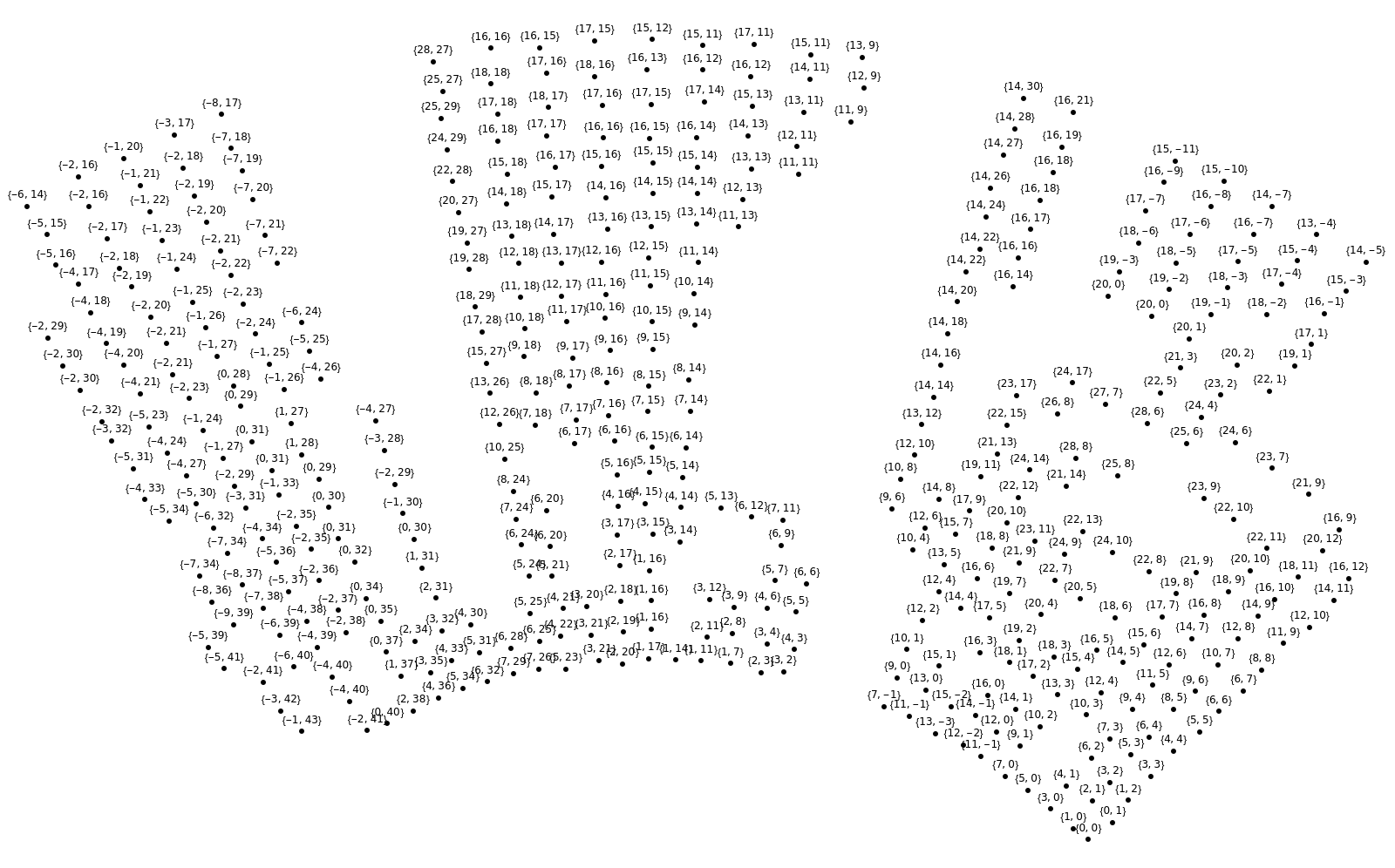 |
Test whether there are duplicate indices:
| In[30]:= |
| Out[30]= |
Wolfram Language 12.3 (May 2021) or above
This work is licensed under a Creative Commons Attribution 4.0 International License