Basic Examples (3) 

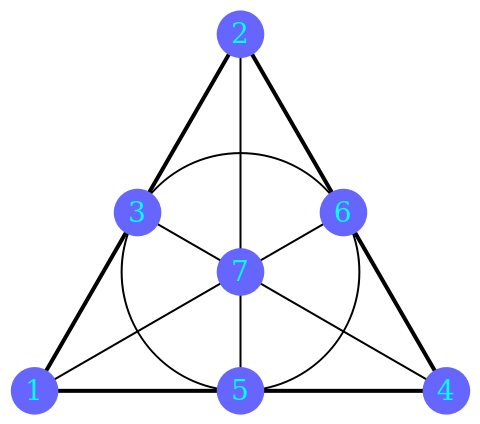
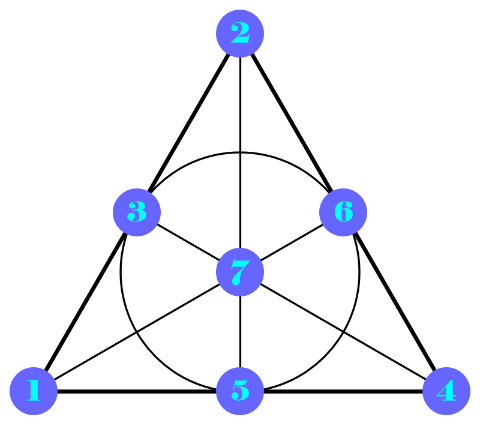
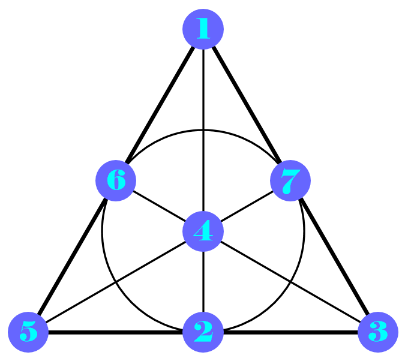
Given the configuration {2,3,1,5,4,6,7}, show its Fano plane diagram:

In[1]:=

Out[2]=

Given the configuration {2,3,1,5,4,6,7}, find all isomorphic permutations that preserves collineation:

In[3]:=

Out[3]=

Verify the number of isomorphism generated is 168:

In[4]:=

Out[4]=

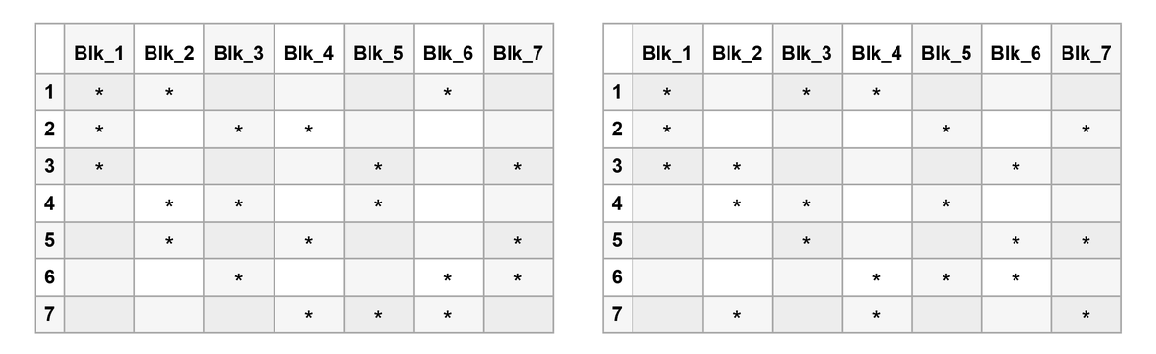
Given the configuration {2,3,1,5,4,6,7}, show the Fano plane block table for it and one of its isomorphisms:

In[5]:=

Out[7]=

Scope (1) 

In the following, block 1 corresponds to the line through triplet {1,2,3} regardless of order. One can find the same triplet on the left side on the diagram. Block 7 has three dots for 3, 5 and 6 which corresponds to the circle (general line) in the Fano diagram and analogously for the other columns:

In[8]:=

Out[9]=

Properties and Relations (2) 

The visual proof below shows the existence of an isomorphic permutation of a given configuration in a trivial way. For instance {2,3,1,5,4,6,7} has the following Fano plane:

In[10]:=

Out[11]=

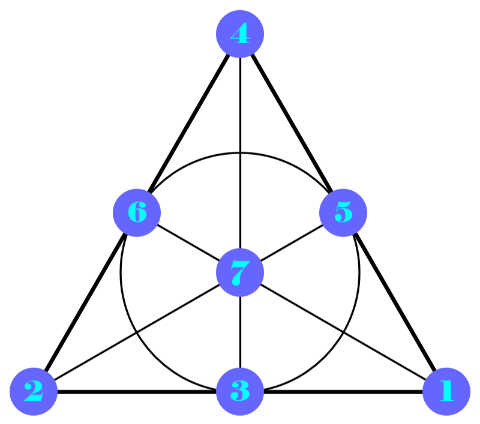
Rotation of the above diagram 120 degrees counterclockwise about 7 will preserve the collinearity of all points:

In[12]:=

Out[12]=

Show the corresponding Fano plane:

In[13]:=

Out[13]=

The cycle structure for permutations of the isomorphic family has 6 conjugacy classes. Use FindFanoPlaneIsomorphism to verify the enumeration given on Wikipedia:

In[14]:=

Out[17]=

One of the permutations is the identity permutation:

In[18]:=

Out[18]=

21 of the permutations have two 2-cycles:

In[19]:=

Out[19]=

Similarly, 42 of the permutations have one 2-cycle and one 4-cycle:

In[20]:=

Out[20]=

56 of the permutations have two 3-cycles:

In[21]:=

Out[21]=

48 of the permutations have a 7-cycle:

In[22]:=

Out[23]=

The 48 permutations are composed of two conjugacy classes: 1) A maps to B, B to C, C to D. Then D is on the same line as A and B. 2) A maps to B, B to C, C to D. Then D is on the same line as A and C. Both classes can be found directly using the reference diagram in Details & Options:

In[24]:=

In[25]:=

In[26]:=

Each class has 24 items:

In[27]:=

Out[27]=

Possible Issues (2) 

The input must be a permutation of {1,2,3,4,5,6,7}. Otherwise the function returns unevaluated with an error message:

In[28]:=

Out[28]=

The property must be one of "BlockTable", "Diagram" or "All". Otherwise, the function returns all isomorphisms only:

In[29]:=

Out[29]=

Neat Examples (2) 

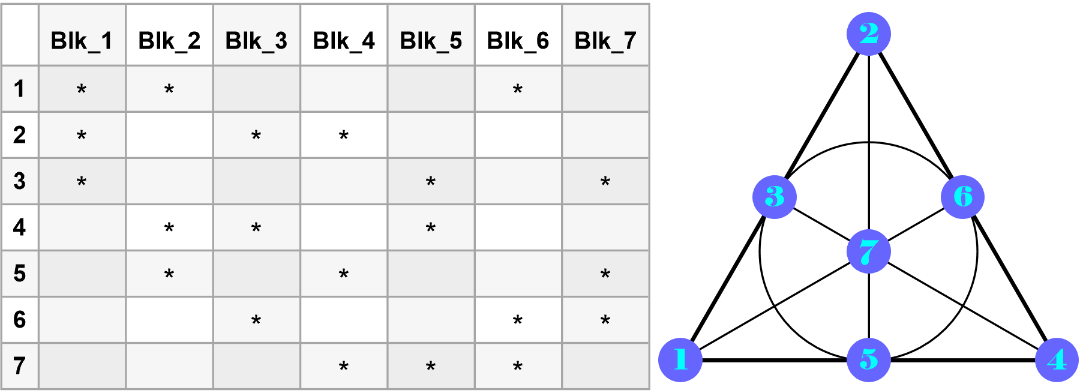
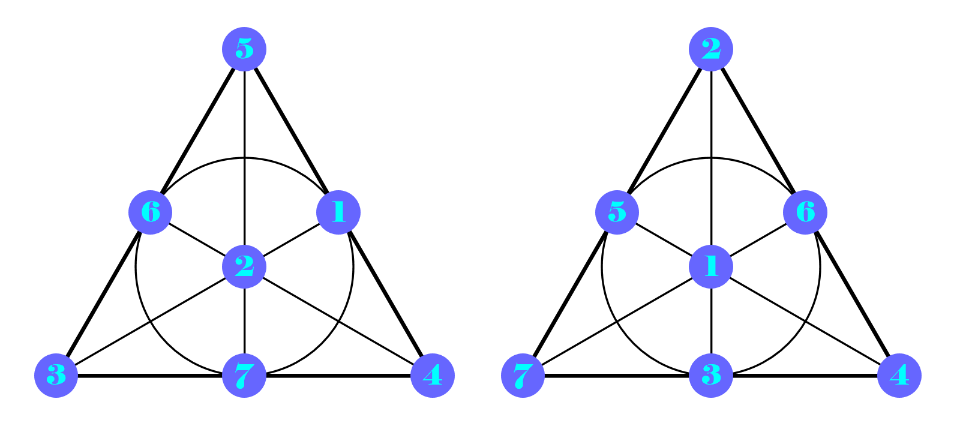
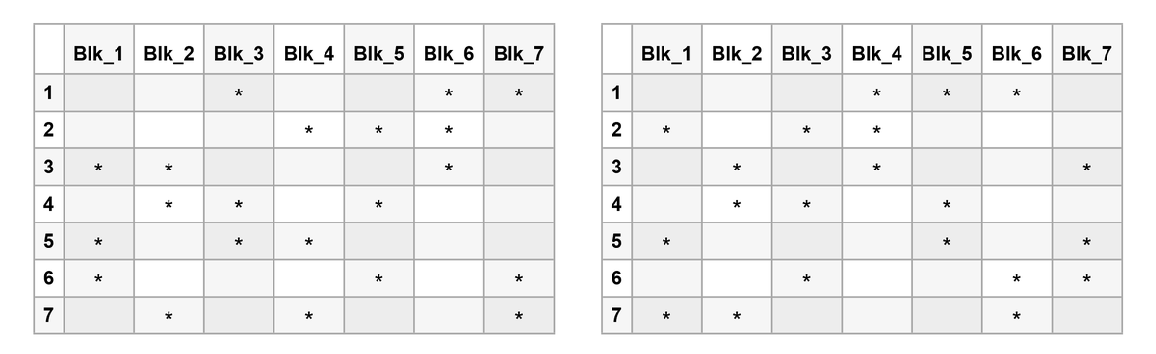
Compare two isomorphic Fano planes for a given configuration with both diagram and block table:

In[30]:=

Out[31]=

The collinearities are identical for both diagrams. For instance, one can find a general line through the triplet {5,6,3} in both diagrams:

In[32]:=

Out[32]=

The two associated block tables are identical up to column swapping: {1→7,2→2,3→5,4→1,5→3,6→4,7→6}, where 1→7 compares the first column in the left table to the seventh column in the right table and so on:

In[33]:=

Out[33]=

Build the Hoffman-Singleton graph. First we generate all even permutation of the given configuration:

In[34]:=

There are exactly 15 non-isomorphic Fano planes:

In[35]:=

Out[35]=

Find 7 collinear triplets in each configuration. Generate blocks or collinear points on the reference Fano plane:

Show the collinear blocks for the first of the 15 Fano planes:

In[36]:=

Out[36]=

Show the Fano plane diagram for this configuration:

In[37]:=

Out[37]=

The Hoffman-Singleton graph has two types of connections: 1. the Fano plane to its 7 collinear triplets 2. a triplet to another disjoint triplet

In[38]:=

In[39]:=

In total there should be 50 = 15 + 35 nodes and 175 edges:

In[40]:=

Out[40]=

Set up customized styles for vertices and edges:

In[41]:=

Mark the Fano planes with triangles and the collinear triplets with circles in the graph:

In[42]:=

Out[42]=

The arrangement of nodes follows a pre-computed Hamiltonian cycle of this graph. The above diagram is isomorphic to the built-in entity:

In[43]:=

Out[43]=

In[44]:=

Out[44]=