Details
An exact cover is a partitioning of a set of elements into disjoint subsets whose union is exactly the original set.
The exact cover (XC) problem gives an original set along with a list of allowable subsets and asks if any selection of the allowable subsets is an exact cover of the original set. It is an NP complete problem, and very similar to graph clique finding (cf.
FindClique).
Here we do not deal with sets and subsets, but rather with binary matrices. The input binary matrix mat lists allowable subsets as rows and set elements as columns, by coding that the kthelement of the original set is also a member of the jth listed subset if and only if matjk=1. Thus a one's row {1,1,…,1} represents a trivial exact cover.
Sometimes the terms items and options are used in place of column and row headers respectively. The exact cover problem can then be stated as follows: Choose a set of options such that every item is included in exactly one option.
If two options are not disjoint, their respective row sum will have a value exceeding 1 in at least one column. Similarly, if neither of two options includes the
kth item, their respective row sum will have a 0 in the
kth column. Let
{ j1,j2,… }∈𝒪 be a set of options. It is an exact cover if and only if the respective row sum satisfies that
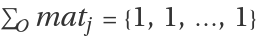
.
Now define a graph whose vertices are options and whose edges indicate pairwise disjunction. Cliques in the graph represent maximal sets of disjoint options, which can easily be tested for the exact cover property once they are found.
FindExactCover has a
Method option for switching between three distinct algorithms:
| "DancingLinksX" | Donald Knuth's algorithm |
| "CliqueToCover" | transforms input to a graph and uses FindClique |
| "BranchAndPrune" | uses a depth-first search |
When using the DancingLinksX method, setting the Heuristic sub-option to either
Automatic or
"Increment" changes the search order:
| {"DancingLinksX","Heuristic"→ Automatic} | Knuth's suggested MRV heuristic |
| {"DancingLinksX","Heuristic"→ "Increment"} | select right-nearest column |
The "MRV heuristic" chooses to cover the next item with the minimal number of associated options.
ResourceFunction["FindExactCover"] ignores empty subsets, i.e. zero's rows of the form {0,0,…,0}.
![With[{coverMatrix = {
{1, 0, 0, 1, 0, 0, 1},
{1, 0, 0, 1, 0, 0, 0},
{0, 0, 0, 1, 1, 0, 1},
{0, 0, 1, 0, 1, 1, 0},
{0, 1, 1, 0, 0, 1, 1},
{0, 1, 0, 0, 0, 0, 1}},
alpha = ToUpperCase[Alphabet[]]},
alpha[[Position[coverMatrix, #][[1, 1]] ]] & /@
ResourceFunction["FindExactCover"][coverMatrix]]](https://www.wolframcloud.com/obj/resourcesystem/images/8af/8af3735d-76fd-44a4-979c-0e02c18aea78/1ccd1453ab73672e.png)
![With[{coverMatrix = Rest[Tuples[{0, 1}, 4][[1 ;; -1 ;; 3]]]},
MatrixForm[coverMatrix] -> MatrixForm[ResourceFunction["FindExactCover"][coverMatrix]]
]](https://www.wolframcloud.com/obj/resourcesystem/images/8af/8af3735d-76fd-44a4-979c-0e02c18aea78/7348d60889835f77.png)
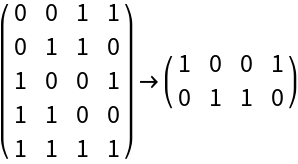
![With[{coverMatrix = Rest[Tuples[{0, 1}, 4][[1 ;; -1 ;; 3]]]},
MatchQ[Total@
ResourceFunction["FindExactCover"][coverMatrix], {1 ..}]]](https://www.wolframcloud.com/obj/resourcesystem/images/8af/8af3735d-76fd-44a4-979c-0e02c18aea78/207a3ae7426679fd.png)
![With[{coverMatrix = Rest[Tuples[{0, 1}, 4][[1 ;; -1 ;; 3]]]},
MatrixForm[coverMatrix] -> Map[
MatrixForm, ResourceFunction["FindExactCover"][coverMatrix, All]
]]](https://www.wolframcloud.com/obj/resourcesystem/images/8af/8af3735d-76fd-44a4-979c-0e02c18aea78/2e463276c783a386.png)
![AbsoluteTiming[SeedRandom[9230482];
ClearSystemCache[]; Reap[
ResourceFunction["FindExactCover"][RandomInteger[1, { 100, 10}],
All, Method -> {"DancingLinksX", "Heuristic" -> #}]
] /. {x_, y_} :> Rule[y[[1, 1]], Length[x]]
] & /@ {Automatic, "Increment"}](https://www.wolframcloud.com/obj/resourcesystem/images/8af/8af3735d-76fd-44a4-979c-0e02c18aea78/72e16f499436190d.png)
![AbsoluteTiming[SeedRandom[9230482];
ClearSystemCache[]; Reap[
ResourceFunction["FindExactCover"][
RandomChoice[{.3, .7} -> {1, 0}, {100, 10}],
All, Method -> {"DancingLinksX", "Heuristic" -> #}] faster
] /. {x_, y_} :> Rule[y[[1, 1]], Length[x]]
] & /@ {Automatic, "Increment"}](https://www.wolframcloud.com/obj/resourcesystem/images/8af/8af3735d-76fd-44a4-979c-0e02c18aea78/612fd4618f6eae7c.png)
![AbsoluteTiming[SeedRandom[9230482];
ClearSystemCache[]; Length@ResourceFunction["FindExactCover"][
RandomChoice[{.3, .7} -> {1, 0}, {100, 10}],
All, Method -> #]
] & /@ {"CliqueToCover", "BranchAndPrune"}](https://www.wolframcloud.com/obj/resourcesystem/images/8af/8af3735d-76fd-44a4-979c-0e02c18aea78/606867f09bee846e.png)
![ListPlot[MapApply[Divide,
Outer[ClearSystemCache[];
First@AbsoluteTiming[ResourceFunction["FindExactCover"][
#1, All, Method -> #2]] &,
Tuples[{1, 0}, #] & /@ Range[5],
{"DancingLinksX", "CliqueToCover"}, 1 ]],
PlotLabel -> Text["Slowdown Factor"],
PlotRange -> {0, 10}]](https://www.wolframcloud.com/obj/resourcesystem/images/8af/8af3735d-76fd-44a4-979c-0e02c18aea78/19c51ccbbf259e23.png)

![With[{tetrisData = {SparseArray[
Automatic, {1, 4}, 0, {1, {{0, 4}, {{1}, {2}, {3}, {4}}}, {1, 1, 1, 1}}], SparseArray[
Automatic, {21, 8}, 0, {1, {{0, 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56,
60, 64, 68, 72, 76, 80, 84}, {{5}, {6}, {7}, {8}, {4}, {6}, {
7}, {8}, {3}, {5}, {7}, {8}, {4}, {5}, {6}, {8}, {3}, {5}, {
6}, {8}, {4}, {5}, {6}, {7}, {3}, {4}, {6}, {8}, {3}, {5}, {
6}, {7}, {2}, {4}, {6}, {8}, {3}, {4}, {5}, {7}, {3}, {4}, {
5}, {6}, {2}, {4}, {5}, {6}, {1}, {3}, {5}, {7}, {1}, {3}, {
5}, {6}, {2}, {3}, {4}, {6}, {1}, {3}, {4}, {6}, {2}, {3}, {
4}, {5}, {1}, {2}, {4}, {6}, {1}, {3}, {4}, {5}, {1}, {2}, {
3}, {5}, {1}, {2}, {3}, {4}}}, {1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1}}], SparseArray[
Automatic, {65, 12}, 0, {1, {{0, 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56,
60, 64, 68, 72, 76, 80, 84, 88, 92, 96, 100, 104, 108, 112, 116, 120, 124, 128, 132, 136, 140, 144, 148, 152, 156, 160, 164, 168, 172, 176, 180, 184, 188, 192, 196, 200, 204, 208, 212, 216, 220, 224, 228, 232, 236, 240, 244, 248, 252, 256, 260}, {{9}, {10}, {11}, {12}, {8}, {10}, {11}, {12}, {7}, {
10}, {11}, {12}, {8}, {9}, {11}, {12}, {6}, {9}, {11}, {12}, {
7}, {8}, {11}, {12}, {8}, {9}, {10}, {11}, {5}, {8}, {11}, {
12}, {7}, {8}, {9}, {12}, {7}, {8}, {10}, {11}, {6}, {8}, {
9}, {12}, {7}, {8}, {9}, {11}, {5}, {8}, {9}, {12}, {5}, {8}, {
10}, {11}, {6}, {8}, {9}, {11}, {7}, {8}, {9}, {10}, {5}, {
8}, {9}, {11}, {4}, {7}, {10}, {11}, {5}, {6}, {9}, {12}, {
5}, {7}, {8}, {11}, {3}, {6}, {9}, {12}, {4}, {7}, {8}, {11}, {
5}, {6}, {8}, {11}, {5}, {7}, {8}, {10}, {6}, {7}, {8}, {9}, {
4}, {7}, {8}, {10}, {5}, {7}, {8}, {9}, {4}, {5}, {8}, {11}, {
4}, {7}, {8}, {9}, {5}, {6}, {8}, {9}, {2}, {5}, {8}, {11}, {
3}, {6}, {8}, {9}, {4}, {5}, {7}, {10}, {4}, {5}, {8}, {9}, {
5}, {6}, {7}, {8}, {2}, {5}, {8}, {9}, {4}, {5}, {6}, {9}, {
4}, {5}, {7}, {8}, {3}, {5}, {6}, {9}, {4}, {5}, {6}, {8}, {
1}, {4}, {7}, {10}, {2}, {5}, {6}, {9}, {2}, {5}, {7}, {8}, {
3}, {5}, {6}, {8}, {4}, {5}, {6}, {7}, {2}, {5}, {6}, {8}, {
1}, {4}, {7}, {8}, {2}, {3}, {6}, {9}, {2}, {4}, {5}, {8}, {
1}, {4}, {5}, {8}, {2}, {3}, {5}, {8}, {2}, {4}, {5}, {7}, {
3}, {4}, {5}, {6}, {1}, {4}, {5}, {7}, {2}, {4}, {5}, {6}, {
1}, {2}, {5}, {8}, {1}, {4}, {5}, {6}, {2}, {3}, {5}, {6}, {
1}, {2}, {4}, {7}, {1}, {2}, {5}, {6}, {2}, {3}, {4}, {5}, {
1}, {2}, {3}, {6}, {1}, {2}, {4}, {5}, {1}, {2}, {3}, {5}, {
1}, {2}, {3}, {4}}}, {1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1}}], SparseArray[
Automatic, {113, 16}, 0, {1, {CompressedData["
1:eJwl0BFzwgEAxuH/7oIgCIIgaHdBEARBEARBEHS7IAi6XRB0rdsFQRAEQRAE
QRAEQRAEQRAEg8FgMBgMBoNBMBgM9uz23j0f4P1d397ddK+CILgP/hciTIQo
MeIkSJIiTYYsOfIUKFKiTIUqNeo0aNKiTYcefQYMGTFmwpQZcxYsWbFmw5Yd
ew4cOXHmgUeeeOaFV95454NPLnzxzc/feSFChIkQJUacBElSpMmQJUeeAkVK
lKlQpUadBk1atOnQo8+AISPGTJgyY86CJSvWbNiyY8+BIyfO/AJZhzT8
"], CompressedData["
1:eJwljo0RgzAIhWMSgQSMrtCVOoILdMkO1g975zveH8HX/XnftZTy3UrhK8c6
rwAOZs4AmNPRTCc0vPF469T0Pa4xUwc4luIbHhoeF/wcLMvMfnJPoOlaXPrX
hzDhCx77yL6T+2no/u+FcFA4Jk+HycN0kh+icynLLTscInNluWfOcTpOJ3P0
oG9R05f0DYzZyDs+Gm4Bd7qTHnvJ1Td+jolHnx9reOhRmfAJNzrkSq7e0fhW
OVw5Vp+cycPkyUdtMhuLdAxfG0sbR7fHS77T6YaH7mAXpuCDRt5y7qD/AFjI
EXE=
"]}, CompressedData["
1:eJxTTMoPSmJkYGA4AiQYR8GQBwDtgQQx
"]}], SparseArray[Automatic, {161, 20}, 0, {1, {CompressedData["
1:eJwl0hFzAgAABeC2C4IgCIKg3QVBEARBEARB0O2CIOh2QdBtQRAEQRAEwWAQ
dLtgMAiCIBgMBkEQBMFgEAyCwSDY1+3dfT/gvXs3dw+391eBQOA58J8gIcJE
iBIjToIkKdJkyJIjT4EiJcpUqFKjToMmLdp06NKjz4AhI8ZMeOSJKTPmvPDK
giUr1rzxzgcbtuzYc+CTL458c+KHX86X8oYIEiJMhCgx4iRIkiJNhiw58hQo
UqJMhSo16jRo0qJNhy49+gwYMmLMhEeemDJjzguvLFiyYs0b73ywYcuOPQc+
+eLINyd++OV8OcG1/oQIEyFKjDgJkqRIkyFLjjwFipQoU6FKjToNmrRo06FL
jz4DhvwBPY9Kng==
"], CompressedData["
1:eJwlj9d5wzAMhMUmAiygihfwShnBC2SJDJ4f1gN1hyv4oPfn9+cTt2374xPA
87pfi2e8yTsQbDGDkzccjZlQQ58EJ6HBU/TufHpm4Z0XeCuZMb/8auiCryD8
7sPzhn+caKBdQrazEH4qXiUjoLb1Ysab3lny8LOS1WZ3Q2M+BJ/cKuR3DqrM
wnHopzwZq86VHEeozxyCb5ncDq8ciXaQM7pLWY5+FPJVhndNWERmJrL01s6h
u2vinbaExSA76dZ+0PN5FrxIlh5eW8z43lOrLEUDlb1j0hvwkfECP0MPXS3z
c2j44r2WHj4i+VzUChpzT/jkGl08mYlD0UZ6fI3OMxmOyD5zCL4GMHIgcyej
9FouX73HVL2jiQX4EjgqOE+eKy2xCNQQd8869wx+1kgJZP5iDZTAAjrfefkf
0A8cmg==
"]}, CompressedData["
1:eJxTTMoPSmJkYGBoYWJgYBwFo2CAAQC7VQSy
"]}], SparseArray[Automatic, {209, 24}, 0, {1, {CompressedData["
1:eJwl0pGTIgAYxuHubiEIgiAIupkgCIIgCIIgCHZugiBoboKg2QuCIAiCIAiC
YCEIgoUgCIIgCILmZiEIgmBhIQiC4J6d+2aeP+D3zvfz959fL98CgcDfwP97
IkiIMBGixIiTIEmKNBmy5MhToEiJZ8pUqFKjToMmLdp06NKjz4AhI8ZMeGXK
jDlvLFiyYs2GLTv2HHjnyIkzFz745MqNO4+veEM8ESREmAhRYsRJkCRFmgxZ
cuQpUKTEM2UqVKlRp0GTFm06dOnRZ8CQEWMmvDJlxpw3FixZsWbDlh17Drxz
5MSZCx98cuXGncfXE3zXT5AQYSJEiREnQZIUaTJkyZGnQJESz5SpUKVGnQZN
WrTp0KVHnwFDRoyZ8MqUGXPeWLBkxZoNW3bsOfDOkRNnLnzwyZUbdx4Efugn
SIgwEaLEiJMgSYo0GbLkyFPgH5PFZGA=
"], CompressedData["
1:eJwlkEl2xCAMRG0GM4jRbtu9zV1yghwhF8j9d/lqL3ggUb9K8PX79/NrlmX5
tsuysp/X/d5Zk/WiGHrWnTX3+33Q7FpP+giH1qwBULhvWg+9Py9B0wHG3N+N
vQ/V7begrU//al31rzPDFHQdY2HnfLeuzLzyUK/95nxWAhqmCU7QNsKyMugq
IdTK7Kmr57ykkE1AhMtopcy7cF8JTsqil6dWdsam3uPMDJ+f/rHhERg4wWTB
46ODh4GfeKpu0HslHgI/vfIMLYRFhk4ZFk3gTH3ADrzmBkvviDwIfjjlCc6E
4LHHBIt55iFwHR+4gv+YgUeF525Y5QlOhOAxN/Qh1iMxhOdMPfGCFzLUu0zO
3agHwZEQPIZHHxnAKYcWj0atXLFJvWV4PoReW/kU+O7Q+03mhiYwhFUexj+1
8mKi+ufueJR7+hW+WfTOw380sOhhBT/VZHrN8iBYgS2eEMPA1sFxv3KmrnAZ
H6GuhofAZTgYPCx6zByDo02waDdZGX59+mhUH9NqQrUEwaDz9Dy9mAwGBkPu
dde7jT2ugCztefbAcv9nYSrD
"]}, CompressedData["
1:eJxTTMoPSmJkYGBwYWZgYBwFo2AUUAQAuqkFMw==
"]}], SparseArray[Automatic, {257, 28}, 0, {1, {CompressedData["
1:eJwl0xGQIgAUBuDudiEIgoUg6GaCIAiChSAIgqC5CYKguQmC5i5YWAiCIAiC
IAiCIFhYCIIgCIIgCIIgCIIgCILgvr17M9/z/5/3fvz68/P3t0Ag8P1rmWeC
hAjzQoQoMeIkSJIizSsZsuTIU6BIiTIVqtSo06DJG++0aNOhS48+A4aMGDNh
ygefzJizYMmKNRu27Nhz4MiJMxeu3Ljz+Aqvg2eChAjzQoQoMeIkSJIizSsZ
suTIU6BIiTIVqtSo06DJG++0aNOhS48+A4aMGDNhygefzJizYMmKNRu27Nhz
4MiJMxeu3Ljz+HcE8hMkRJgXIkSJESdBkhRpXsmQJUeeAkVKlKlQpUadBk3e
eKdFmw5devQZMGTEmAlTPvhkxpwFS1as2bBlx54DR06cuXDlxp0HgSf5CRIi
zAsRosSIkyBJijSvZMiSI0+BIiXKVKhSo06DJm+806JNhy49+gwYMmLMhCkf
fDJjzoIlK9Zs2LJjz4EjJ85cuHLjzuPp//M/8xdv+IFD
"], CompressedData["
1:eJwl0Et24zAMRFHrb4nUl5KT2Jn0lnoJ2UD2P+sL94AHRBH1APDPz+/fn/p2
u7Xt7VaJX8/X9+V8upxicU73D0IRj9Av+unQTsUPj4f7HjVMi/eD8aAX5l2c
1W9RV6Lm4r9es9odcAc4StRez809867ifkT9+VrUi8/MO7vLX5tm+xG+E/t6
JZxtD095zjziV+LP7vLnqvmmET08F/05YczL9b1quhkk84qfE05yl3vXXz09
vGcKTT7iZUvhXKthEr/4MeCNeJOcpsY8fN4eGGUKTX63YLIo3qnHNWH0eKPo
7s08Fss88/L2H2PowbAsTsE+R4t1OAPG3V3+mJJ5DJZ4sub30Nzxr9HSOAc+
/3I5Z4vXB2vaPrDLpFnK4V0K3o5/3i2Ms2PzzufAK5YGr8Pq5TR160OPY0rB
mPV88ws2by49r3jUeC1WJ6cV/H3U2Fv4lu4/++h9KOY2GqzjF/fK5zV4rZym
xjw83sI/t6HJ9dg7S2Mtd0O1GOJW4zXucu9m4qGv/LkJTa7H1loca8ZfGv7a
EelmsVinvh/e3lSHHn7LYmTcubZU5Yhr0+pvkFZtp2EVWviaNzdh8gyLM9fN
uOHkBrjton7IGFNVv3kTlvp+dnJV31eM1LRR2+PFe2eOLqmfahD3eBvUjjWw
Q29D7ytmZ3TutE5s/wFJwzvs
"]}, CompressedData["
1:eJxTTMoPSmJkYGBgYWFgYBwFo2AUjGgAAOt9BbQ=
"]}], SparseArray[Automatic, {305, 32}, 0, {1, {CompressedData["
1:eJwl0xGQIgAUBuDudiEIgiAIupkgCJqbIAiCIAiamyAImpsgaO6CIAiCIAiC
IAiCIAiCIAiCIFhYCBaCIAiChYVg4b6dezPf8/9/8378/vvrz7dAIPDza5ln
goQIEyFKjDgJkqRIkyFLjjwFipQoU6FKjToNmrRo06FLjz4DhowYM2HKjDkL
lqxYs2HLjj0Hjrzwyok3zly4cuPOOx88+PwKr4NngoQIEyFKjDgJkqRIkyFL
jjwFipQoU6FKjToNmrRo06FLjz4DhowYM2HKjDkLlqxYs2HLjj0Hjrzwyok3
zly4cuPOOx88+Py6/3f5CRIiTIQoMeIkSJIiTYYsOfIUKFKiTIUqNeo0aNKi
TYcuPfoMGDJizIQpM+YsWLJizYYtO/YcOPLCKyfeOHPhyo0773zw4JPAk/wE
CREmQpQYcRIkSZEmQ5YceQoUKVGmQpUadRo0adGmQ5cefQYMGTFmwpQZcxYs
WbFmw5Ydew4ceeGVE2+cuXDlxp13Pnjw+fT/+Z8JEiJMhCgx4iRIkiJNhiw5
8hQoUqJMhSo16jRo0qJNhy49+gwYMmLMhCkz5ixYsmLNhi079hz4B6nBlVM=
"], CompressedData["
1:eJwl0VmimzAMQNGEMQFsCGbInNctdQndQDfZhfUQPhxLsn2vUH79+fv7T3Y4
HP4Vh8PR/np/fp5+rvbVWqyHwqq2WLO1Xj8/d8VFfbaW1V0Ppm/8/twczs4n
awZYPB68Sd/89e7dn9xZ1utPsk+gM5j803s/7mfvCTx6nwBnktGeSCZw+Tti
DRiX/fzVi+WfRBzmzXP9TBoYiROh+BUweyzxM9rFzr/vr920+dZ30tBFEyOx
+NnhRZx+0C95EMvdud1x1jZtvuXVD+tnwBk12e/7o8UOeNFHx7127+RqepqX
hkf+jD0+1kWzJ564x/eGo8MLBhH22q2Vqz34Nt58NgC1R4g8mDUX/sJ57TXU
YnYG0n196SG/822sSX7vAj5OxYE7c61RMyf8xiBag2m/nvEuv/Fsjqv81nbY
ONFwSg7siWsJGlFba57GgJr9zsK1edRwNRA0WeDjJp6504jaUnGcMM8GdN7v
zbVcbeWcuPQwrOfmcus0nG8OTbaakc8lT40tniq7eOHcOAOfHvql1Wi28TXX
aEY+FdgVXu1PkKdSLJ95RqyehzvO9alfT1iNpo/+gHqPU85R4lYGVO21sZCr
6S1EviSfqpoD76zpat/HjKPAKw2o3GuXXK6W+DZW4BrVUllx4OFGrqHWTI5V
GEzx9bRJPvJsnE4+FiU2Bl7g6CsNZD4+N5D8y25G+QU7ii95gedtZRhYHXYs
SeV9ZhDZfhZxQ5bjEJWawWgxQ0Emj0cffdzPAmZ3zM6XQgMYXU4gdrfqMLY7
p5zImzYDFLtTtt407tQZsOWs2M6qI4jVWGe10l78B215URQ=
"]}, CompressedData["
1:eJxTTMoPSmJkYGA4wsLAwDgKRsEoGAVDGAAAEWQHNA==
"]}], SparseArray[Automatic, {353, 36}, 0, {1, {CompressedData["
1:eJwl1CGwKQgUBuC7++7OCIIgCIKdEQRBEARBEATB7AiCYN4IgnlPEARBEARB
EARBEARBEARBEIQbbrhBEARBEARBEN53Z8/Md/p/zpzz78/f//366+3t7ed3
U+8ECBIiTIQoMeIkSJIiTYYsOfIUKFKiTIUqNeo0aNKiTYcuPfoMGDJizIQp
M+YsWLJizYYtO/Yc+OCTL46cOHPhyo07D568vsObwTsBgoQIEyFKjDgJkqRI
kyFLjjwFipQoU6FKjToNmrRo06FLjz4DhowYM2HKjDkLlqxYs2HLjj0HPvjk
iyMnzly4cuPOgyev7/3/LT8BgoQIEyFKjDgJkqRIkyFLjjwFipQoU6FKjToN
mrRo06FLjz4DhowYM2HKjDkLlqxYs2HLjj0HPvjkiyMnzly4cuPOgycv3n7I
T4AgIcJEiBIjToIkKdJkyJIjT4EiJcpUqFKjToMmLdp06NKjz4AhI8ZMmDJj
zoIlK9Zs2LJjz4EPPvniyIkzF67cuPPgyevH/8f/ToAgIcJEiBIjToIkKdJk
yJIjT4EiJcpUqFKjToMmLdp06NKjz4AhI8ZMmDJjzoIlK9Zs2LJjz4EPPvni
yIkzF67cuPPgyev78f0jPwGChAgTIUqMOAmSpEiTIUuOPAWKlChToUqNOg2a
tGjToUuPPn8AmeCrhQ==
"], CompressedData["
1:eJwdkdmBozAQRG1ujE5AJ+MTR7QhTAKbxAa+T/rQdHfJqlf0vH///vltLpfL
v/5yuVLfn/P74s9BzZzEeSJktMSJnAdCKtpxfiM1cFLm9zy6cxnLPY8D1XMi
JgmDHy5X3oTyG8w81fLOUQPGMZV3x5dzWt57fh9i1T6O3uCzUz3AEItHPjkf
g5fD3IeqvVc8dmaNp6VnPjdmRxgfimcq+kl9a/ydr9rL4qfwNlT6z04w54tv
5Bvygf6hfyk4u6v60+Al8dVU+rddj+9GyJ1AjqD4Zu5ghKeEY9d8rnhte71/
aLxhHQKWomd+GZYC69gJDCOhw/MPAdNYsuPJfFf4w8wzzAWmZEZ7ahYFM298
AIyI/qS/LzC1iW+DJznI4H4kDJhpgnljSYIZ7aFYHtxElsOulRdE1cNL40mO
LPCHF0d4Cz3zXbJAeJEM2RAUhufuPsOTyj8VPmRIC0uCEwY4sI8bM9qPYJlw
AvykTeGs5e6HmqfClO4h8SRHuUswfQ+TDHlhibA8GaLShWMzJ42FJ/a7IAwZ
ih5nfOG5Dh4Z+P71QMs3FgnPkSNIVTim3GVqHGDelo2MVQ8T/i1M+OzAZmY4
zgtZOJod2BU90YceLhmK7kc8Gziw+X6TmOPEPxG2Wwgp+AD8LXeR3nfwptnm
GT/45d4N+MNbr/zTyMAOdEQLI8uEuS58ACyDDle6FvY48S34Mu89DLiWHOxA
BWY/sESY9sZHwNDonn5vYA6jjiN+5CCD2Dr84Rn4e0vP7HoWCc+QYZ3mylFt
1VUY8INvW7xh6YZKv3csD46GbUfC4S2bqkvf8x6uaVgM/upKpd9aFoevgmeG
sfjO7GHZqLbthOvwgFl00xY/FoSnhKX7oXhOlmOadtlbgLCKpvEWVxaCl4Ch
ur74jIajr80Nbp0VfrLtyruB3NNMRauz5L1oMG2B8duJilZn9I4Mw0gt/XLF
CH2glv6G1lO7/yxFaD0=
"]}, CompressedData["
1:eJxTTMoPSmJkYGBoYWVgYBwFo2AUjIJRMGAAAGSHB7U=
"]}]}}, Labeled[
ListLogPlot[Outer[AbsoluteTiming[
ResourceFunction["FindExactCover"][Normal[#2], All, Method -> #1]][[1]] &,
{"DancingLinksX",
{"DancingLinksX", "Heuristic" -> "Increment"},
"BranchAndPrune", "CliqueToCover"},
tetrisData[[1 ;; 5]], 1], PlotStyle -> {Red, Orange, Darker@Green, Blue},
PlotLabel -> "First terms of Tetris Timing Test "],
Grid[{{Spacer[10],
Red, Text@"DancingLinksX", Spacer[50],
Blue, Text@"CliqueToCover"},
{Spacer[10],
Orange, Text@"DLX + Increment", Spacer[50],
Darker@Green, Text@"BranchAndPrune"
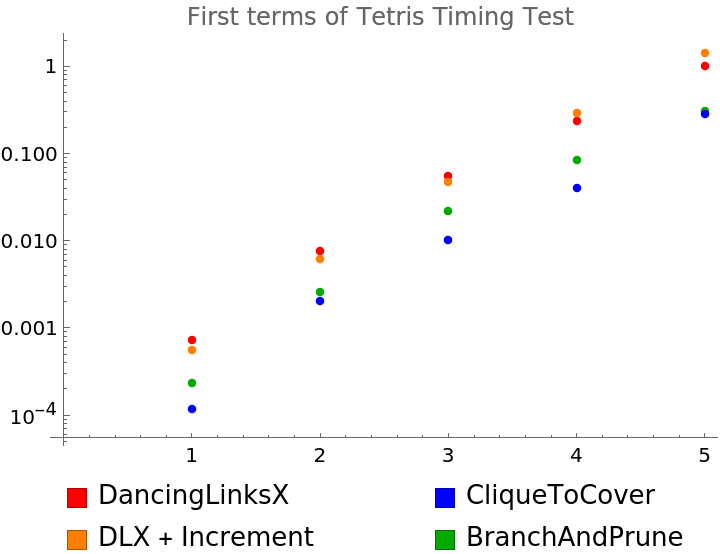
}}, Alignment -> Left]]]](https://www.wolframcloud.com/obj/resourcesystem/images/8af/8af3735d-76fd-44a4-979c-0e02c18aea78/1ce9a60c9f2be1f9.png)
![With[{timingsData = {{{0.000126, 1}, {0.001624, 4}, {0.016606, 23}, {0.071039, 117}, {0.51405, 454}, {7.019132, 2003}, {103.378979, 9157}, {
DirectedInfinity[1], 0}, {
DirectedInfinity[1], 0}}, {{0.000273, 1}, {0.003343, 4}, {0.02751, 23}, {0.094647, 117}, {0.336667, 454}, {1.384281, 2003}, {7.586634, 9157}, {44.559014, 40899}, {251.11148, 179399}}, {{0.000788, 1}, {0.008222, 4}, {0.058785, 23}, {0.220384, 117}, {0.901261, 454}, {3.972747, 2003}, {18.658699, 9157}, {88.163207, 40899}, {405.350752, 179399}}, {{0.000613, 1}, {0.006324, 4}, {0.047467, 23}, {0.259825, 117}, {1.317492, 454}, {7.347735, 2003}, {42.384888, 9157}, {
DirectedInfinity[1], 0}, {
DirectedInfinity[1], 0}}}}, Labeled[
ListLogPlot[Map[First, timingsData, {2}],
PlotLabel -> "More terms of Tetris Timing Test",
PlotStyle -> {Blue, Darker@Green, Red, Orange}],
Grid[{{Spacer[10],
Red, Text@"DancingLinksX", Spacer[50],
Blue, Text@"CliqueToCover"},
{Spacer[10],
Orange, Text@"DLX + Increment", Spacer[50],
Darker@Green, Text@"BranchAndPrune"
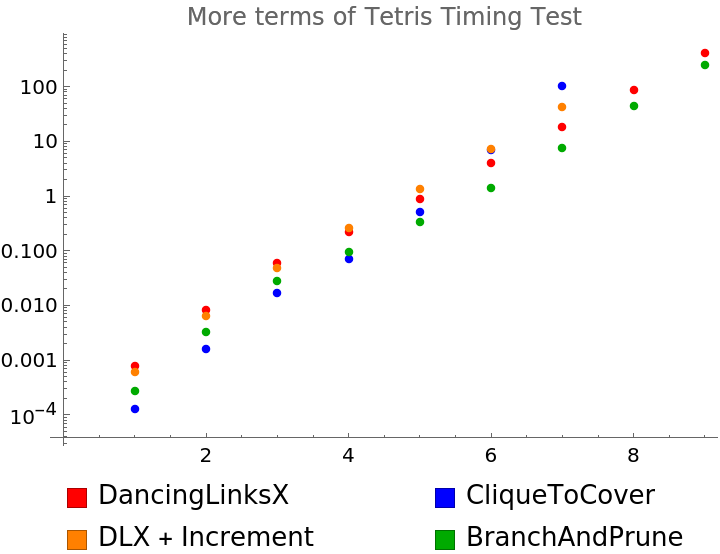
}}, Alignment -> Left]]]](https://www.wolframcloud.com/obj/resourcesystem/images/8af/8af3735d-76fd-44a4-979c-0e02c18aea78/7d602a8098aa8d6a.png)
![With[{
template0 = ArrayPad[ConstantArray[1, {2, 2}], 3],
res1 = ResourceFunction["FindExactCover"][
Normal[SparseArray[Automatic, {1568, 72}, 0, {1, {CompressedData["
1:eJwl2HEoeF2ewGFrzW9nZ6w11hprjTVGkiRJkiRJkiRJkiRJkmQlSZIkSZIk
SZIkSZIkSZIkSZIkSZIkSZIkSZL2efc99XT+vbdPt3Pu9+91/1vW8k8BAQF/
/xXw/+u3LZgwIokhniRSySCbPAopoZwqammgmTY66aGfIUaZYJo5FllhnS12
OeCYMy654Z4nXvngm0AP/UdCCCeKWBJIJo1McsiniFIqqKaORn57+Xa66GWA
YcaYZIZ5llhlg232OOSEc6645YFn3vjkh6DAgIA/EUoE0cSRSArpZJFLAcWU
UUkN9TTRSgfd9DHICONMMcsCy6yxyQ77HHHKBdfc8cgL73wR8M/6E0wYkcQQ
TxKpZJBNHoWUUE4VtTTQTBud9NDPEKNMMM0ci6ywzha7HHDMGZfccM8Tr3zw
TWCQ/oQQThSxJJBMGpnkkE8RpVRQTR2NtNBOF70MMMwYk8wwzxKrbLDNHoec
cM4VtzzwzBuf/BD0B/0JJYJo4kgkhXSyyKWAYsqopIZ6mmilg276GGSEcaaY
ZYFl1thkh32OOOWCa+545IV3vv7w+8f/i2DCiCSGeJJIJYNs8iikhHKqqKWB
ZtropId+hhhlgmnmWGSFdbbY5YBjzrjkhnueeOWDbwL/RX9CCCeKWBJIJo1M
csiniFIqqKaORlpop4teBhhmjElmmGeJVTbYZo9DTjjnilseeOaNT34I+qP+
hBJBNHEkkkI6WeRSQDFlVFJDPU200kE3fQwywjhTzLLAMmtsssM+R5xywTV3
PPLCO18E/Kv+BBNGJDHEk0QqGWSTRyEllFNFLQ0000YnPfQzxCgTTDPHIius
s8UuBxxzxiU33PPEKx98E/gn/QkhnChiSSCZNDLJIZ8iSqmgmjoaaaGdLnoZ
YJgxJplhniVW2WCbPQ454ZwrbnngmTc++SHoz/oTSgTRxJFICulkkUsBxZRR
SQ31NNFKB930McgI40wxywLLrLHJDvscccoF19zxyAvvfP3594P/F8GEEUkM
8SSRSgbZ5FFICeVUUUsDzbTRSQ/9DDHKBNPMscgK62yxywHHnHHJDfc88coH
3wT+m/6EEE4UsSSQTBqZ5JBPEaVUUE0djbTQThe9DDDMGJPMMM8Sq2ywzR6H
nHDOFbc88Mwbn/wQFKI/oUQQTRyJpJBOFrkUUEwZldRQTxOtdNBNH4OMMM4U
syywzBqb7LDPEadccM0dj7zwzhcB/64/wYQRSQzxJJFKBtnkUUgJ5VRRSwPN
tNFJD/0MMcoE08yxyArrbLHLAceccckN9zzxygffBIbqTwjhRBFLAsmkkUkO
+RRRSgXV1NFIC+100csAw4wxyQzzLLHKBtvsccgJ51xxywPPvPHJD0F/0Z9Q
IogmjkRSSCeLXAoopoxKaqiniVY66KaPQUYYZ4pZFlhmjU122OeIUy645o5H
Xnjn6y+/X/p/EUwYkcQQTxKpZJBNHoWUUE4VtTTQTBud9NDPEKNMMM0ci6yw
zha7HHDMGZfccM8Tr3zwTeB/6E8I4UQRSwLJpJFJDvkUUUoF1dTRSAvtdNHL
AMOMMckM8yyxygbb7HHICedcccsDz7zxyQ9B4foTSgTRxJFICulkkUsBxZRR
SQ31NNFKB930McgI40wxywLLrLHJDvscccoF19zxyAvvfBHwn/oTTBiRxBBP
EqlkkE0ehZRQThW1NNBMG5300M8Qo0wwzRyLrLDOFrsccMwZl9xwzxOvfPBN
YIT+hBBOFLEkkEwameSQTxGlVFBNHY200E4XvQwwzBiTzDDPEqtssM0eh5xw
zhW3PPDMG5/8EPRX/QklgmjiSCSFdLLIpYBiyqikhnqaaKWDbvoYZIRxpphl
gWXW2GSHfY445YJr7njkhXe+/vr7D/8vggkjkhjiSSKVDLLJo5ASyqmilgaa
aaOTHvoZYpQJppljkRXW2WKXA44545Ib7nnilQ++Cfwv/QkhnChiSSCZNDLJ
IZ8iSqmgmjoaaaGdLnoZYJgxJplhniVW2WCbPQ454ZwrbnngmTc++SEoSn9C
iSCaOBJJIZ0scimgmDIqqaGeJlrpoJs+BhlhnClmWWCZNTbZYZ8jTrngmjse
eeGdLwL+W3+CCSOSGOJJIpUMssmjkBLKqaKWBpppo5Me+hlilAmmmWORFdbZ
YpcDjjnjkhvueeKVD74JjNafEMKJIpYEkkkjkxzyKaKUCqqpo5EW2umilwGG
GWOSGeZZYpUNttnjkBPOueKWB55545Mfgv6mP6FEEE0ciaSQTha5FFBMGZXU
UE8TrXTQTR+DjDDOFLMssMwam+ywzxGnXHDNHY+88M7X334f9v0imDAiiSGe
JFLJIJs8CimhnCpqaaCZNjrpoZ8hRplgmjkWWWGdLXY54JgzLrnhnide+eCb
wP/RnxDCiSKWBJJJI5Mc8imilAqqqaORFtrpopcBhhljkhnmWWKVDbbZ45AT
zrnilgeeeeOTH4Ji9SeUCKKJI5EU0skilwKKKaOSGuppopUOuuljkBHGmWKW
BZZZY5Md9jnilAuuueORF975iv1tCKw/wYQRSQzxJJFKBtnkUUgJ5VRRSwPN
tNFJD/0MMcoE08yxyArrbLHLAceccckN9zzxygffBMbpTwjhRBFLAsmkkUkO
+RRRSgXV1NFIC+100csAw4wxyQzzLLHKBtvsccgJ51xxywPPvPHJD0H/0J9Q
IogmjkRSSCeLXAoopoxKaqiniVY66KaPQUYYZ4pZFlhmjU122OeIUy645o5H
Xnjn6x+/D/p/EUwYkcQQTxKpZJBNHoWUUE4VtTTQTBud9NDPEKNMMM0ci6yw
zha7/B/V1nYA
"], CompressedData["
1:eJwt2VdWI9GSheFKKfOko/DeSFgZkAFZkMXD8x3CnUBPsYfW+9/VL6oXrVWf
IiP2iZNc/fd//vPfyp8/f/739s+fSP9Gfze3tnciPnYjPvYiPvajg8Oj45OI
j9OIj7OIj/Poola/vIr4uI74uIn4uI2eBsPROOJjEvExjfh4jl5m88Uy4mMV
8bGO+HiN3t4/Pr8iPr4jPn4iPn6jvwcXdw/R5mGt0Ym2jurNbrR7et3qRXtn
N+1+tH9+e/8Y8ZWniK8MIr4yjPjKJOIr04ivPEd85SXiK7OIr8wjvrKK+Mo6
4iuvEV95i/jKe8RXPiK+8h3xlZ+Ir/xWNrdUicrWtipR2d5RJSo7u6pEZXdP
5ajs7asmlcMjVaVydKyqVI5PVJXKyamqUjk9U2kqZ+eqT6VWv2s0Kze3rfZ9
pdF86HQr7fte/7HS6apylV5fxar0H1WxymComlWGI9WsMhqrZpXxRDWrTKYq
XGX6rOpVZnPVrzJfqH6VxVL1qyxXql9ltVYRK+tXVbLydxP55hbyrW3k2zvI
d3aR7+4hPzhEfniE/OgY+fEJ8pNT5KdnyC9qyK9vkN81kLfayB86yDtdPXP5
kT8NkA+GyIcj5KMx8vEE+WSK/GWGfDZHPl8gXyyRL1fIV+t/8i3Lty3fsXzX
8j3L9y0/svzY8hPLTy0/s/zc8rrkV9Dlv7W/af+9/V1X/tHyoeUjy8eWTyyf
Wv5s+dzyheVLy1eWry1//Sc/OETuntlxz+y6Z/bcM2oX5Bc15O6ZE/fMqXvm
zD2jdkF+11DPXLryahrkDx3kvT7ypwFy9cwT7YLcPTN2z0zcM1P3jNoF+ds7
cvfM0j2zcs+s3TNql8omrVDZclW3XdUdV3XXVd1zVfdd1UMaonLk2p65tueu
bY3mqNRd4RtapHLrOjdolErT1W7TKJV717xDu1S6rnzP1e672o+u9oBGqQxd
85FrPnbNJ6751DV//ldzyzct37J82/Idy3ct37P8wPJDy08tP7P8wvKa5deW
31h+Z3nD8pblbcsfLO9Y3nXP9CzvW/5k+cDyoeUjy8eWTyyf/n+3HBzWPKF1
T+ilJ/TKE3rtCZVcRb/1nDY8p03PZsuzKb9+1r0nVH79rK7nVH79rEdPq/z6
WUPPrPz6Wc+e3Jknd+7JlVw/69Xz++75/fD8fnp+vzy/355fyfUT/8kvLK9Z
Xrf80vIry68tv7H8zvKGE6ZpecvytuUPlncs71net/zJ8oHlE8unlr9YPrN8
Zfna8jfL3y3/sPzT8i/Lvy3/qf4lz6ub5Hl1izyvbpPn1R3yvLpLnlcPyPPq
IXlePSLPq8fkefWEPK+ekufVC/K8ek2eV+/I82qLPK8+kOfVHklefSLJqwOS
vDokyasjkrw6JsmrE5K8+kKSV2ckeXVOklcXJHl1SZJXVyR5lVSRWakis1JF
ZqWKzEoVmZUqMitVZFaqyKxUkVmpIrNSRWalisxKFZmVJzIrT2RWnsisPJFZ
eSKz8kRm5YnMyhOZlScyK09kVp7IrDyRWXkis/JEZuWJzMoTmZUnmPXgZdaD
l1kPXmZNpcxqX5nVBNW9fTWB5GoCydUEcqoJqup4VVUd/9CpquNVW/V6r19V
r6vC6vWnQVW9rjqr1yfTqnpd1Vavv8yq6nXVXL2uCqvXVWH1+tu7fpHmUb9I
86hfpHnUL9I86hdpHqvqftf5wOZDm49sPrb5xOZTm89svrC5ZvO1zTc239nc
sLllc9vmB5s7Nvds7tv8ZPPA5onNU5tfbJ7ZPLd5YfPS5pXN65/feJtFLd5h
UYt3WdTiPRa1eJ9tLT5mXYtPWNfiU9a1+Ix1LT5nZ4t7LGpxn0UtfmRbi0es
a/GYdS2esK7FU9a1+JmdLV6wtMVLlrZ4xdIWr1na4lc2t/ivJZuWbFmybcmO
JQeWHFpyZMmxJSeWPLA+xh3Wx7hr1ZMlA0uGlowsGVvyYsnMkrklC0uW/yQa
FUk0KpJoVCTRqEiiUZFEQkkklERCSSSURMzbGForhtaOod3H0CSRShLRJFGt
JFHBJJFQEgklkVASCSUR85/kwJJDS44sObbkxJILS2qW1C25tOQqpmB3MQVr
WNW05MWSmSVzSxaWLC15s+Tdkg9LPi350nPRlOm5aMriPaYs3mfK9EQ0ZXoi
mrL4jCmLz5myuMaUxXWmLNbmrCdyw6zFt8xa3GDW4iazFmtn1tNpM3HxPROn
56iJ03PUxMU9pizuM2XxI1MWs+E38EjCbt/GIwlbfQePJOzzfTySsMkP8EjC
Jj/CIwmb/HPMDj/DIwk7/AKPJOzwrzEL/jseSVjwP/FIwoLP09H/pqejX68n
ov8z3oUS73HN0NPR/6mno/9TT0T/Z3wKKD7jgqGno/9TT0f/p/pE/2d8DSi+
4WoR3wGKG4DiFpS4zXUifoASd6DEPRBxn1tGTPLcxSSPntE2HtKmFZM27Zi0
eYhJGz2pYzxkTi8mc/oxmfMUkzl6Xpd4SB49r1s8JM9LTPLMYpJHT+oeD8nz
FpM87zHJo2ek5PlJOB6PE47Hk4Tj8TTheDxLOB7PEw7Gy4SD8SrhYLxOOBhv
Eg7G24Sjb5T0aMqEC81zwgG4SDgAlwkH4CrhAFwnHICvCUffZ8LR95Vw9H0n
HH0/CUffb7JpyZYl25bsWLJryaElR5YcW3JiyaklHUu4moyTniUDS4aWjCwZ
WzKxZGbJ3JKFJUtLVpYwxUcJUywPV5GEKZaHq0gCs57AlIdLSAJTHi4hCcxm
Aq2VQGsn0OYJNHm4ZiQUTB6uGQnMjwSmPFwwEpjycMGw5NCSI0uOLTmx5NSS
miV1Sy4tubLk2pJGQsGalrQsmVkyt2RhydKSlSXvlnxY8mnJlyXfCcd7I+F4
byYc6a2EI72dcKTfJ4RNJyFsuglh008Im8eEsBkkhM0wIWymCWHznBA2s4Sw
mSeEzSohbNYJYfOaEDbvCWHzkRA23wlh85MQNu4TJAwqvYGEQU1YnO/pEyQM
Kr3R6iUw5WFQE5jyMKgJTHkY1ASmPAxqAlMSBpW+QiLmB32FZMLUwFSfcMFQ
ZTSLqgzPfZdrhirDcyf2HhJir5MQe5JwzUiIvaeE2BskxN4kIfamCbH3khB7
VIaeIfaoDH1C7L0lxB6VoWeIPSrjPiEyEu5ESI79jM78jBQZCUwkdT+jSypD
ZCQw8SgyEph4FBkJTDyKjATmLIGJRJGRwEQy9DMa+RlN/Yy0oIQtFpSwzYIS
dlhQwi4LSthjQQlHLCjhmAUlnLCghFMWlHDGghJ0/jWaoceCEvosKGHIghJG
LChhzIISJiwoYcqCEuYsKGHBghKWLChhxYIS1iwogaP4MHAU49m1Z88eUQJH
cS1wFOM5tefMHlECR3EjcBTjESVwFM8CRzGeiT1Te0QJHMXvgaMYz8qetT2i
hL8sSfJQjS2WJHmohs6gs/NwwJIkD9U4YkmSh2qotW9ug1q4fR8eWJVCh1Up
PLEkyUM1hixJ8lANtef6NbywJMlDNeYsSfJQDU3Rz68kW5ZsW7Jjya4le5Yc
WXJsyYklp5aoUwKLUjuwKOERRZKhJSNLxpZMLJlaMrdkYcnSkpUlOosDeXIX
yJNG4LrQDORJK5An7UCePATypBPIk14gT/qBPHkK5MkgkCeTQJ5MA3nyEsiT
WSBPloE8WQXyZB3Ik7dAnrwH8uQrkCffgTxRnzA7gautJMxO4DorCbMTYErC
7ASY3QBTHmYnwJSH2Qkw5WF2Akx5mJ0AUxJmJ8CUhNkJMCVhdsKjZ4c8aQTy
pBl2VP5WIE/agTy5D+RJJ5An3UCe9AN58hjIk0EgT4aBPJkG8uQ5kCezQJ7M
A3myCOTJOpAnr4E8eQ/kyUcgTz4DefITyBP1CRkryZElp5acWXJuSc0SZWyA
2Qsw8dza07CnaU/bnnt7OvbofwswkTxaMrBkaMnIkqklyth0ixUk3WYFSXdY
QdJdVpB0jxUk3edunh5xN0/PuZunde7m6S1387TJgpK2WFDSNgtKes89Pe2y
pqQ9VpO0z2qSPnI3T4csKOmIBSUds6CkExaUdMqCkj5zN095RvWUZ3SZkvlX
suHhed2kPK/blCfVTHlG9ylPp5vyXB5Tnsgw5YmMUp7IOOWJPKc8i3nKs1ik
PItlyrN4TVlmP1KW2c+UZfZLNjxjJjplsZWHdTZlouXRRMvDapsy0fKw2qbM
dTNlllsps9xOufrIxhNMmeteylz3Uy5AcvLs0hZPLWXSVSueVMq8y8MzSpl3
eTgTU+ZdHj8v3l1c4Dms4ZGNteUSj2ysLdd4Lu5SlpdGyvLSxCMb7yseUtaW
Tsra0sUjG+8unvD0JnieXvBMVnhe3vDM3vHIxlLziUc2lprvbIu3r9k2b1+z
Hd6+Zru8fc32ePua7fP2NTvi7Wt2zNvX7Jy3r1mdt6/ZLW9fsyZvX7M2r+yz
e97BZl3ewWY93rtmfd67Zo+8d82GvHfNRrx3zca8d80mvHfNprx3zZ5575rx
wvgi44WxVFq4pdLCLZUWbqn2FT0Z5LsMslQiNzOYrQzmQwazk8HsZTCfMpiT
DOZLBlMqMVcZzLeMV8VSaR2XSmSpRJZK5O+MSa9nTPpltkXyZ9skf8bU32RM
/W3GvDczJr2dMen3GTPezZjux4y5HmbM9Shjrp8zJnqeMdGLjIleZkz0a0bk
fGREzmdG5HxlI86FbMy5kBE/vxlnpTxQMo4peaBkHFPyEEAZ5GYGs5XBlIro
yWB2M5j9DKZssDKYUgHKYC4ymPJAyWDKAyXjEJMHSgb5N+d+VM+5H13m3I+u
cu5H1zn3o5uc14e3ORHVzImlVk4stXNi6T4nlro5sfSYE0vDnFh6zomleU4s
rXJiaZ0TS685sfSRc3v6zLk9feVE1HdORP3kRNRvzrlZzzk3L3POzauc12zX
OTv5Tc4ZeptzejZzzs37nBOzm3NWPuacksOcU3KUc0pOc07J55zzcZ5zPi5y
zsd1zvn4mnOt/8i51n/mvEj7ynmR9p1zxf/JueL/5rwFushZcGo5C45qxU0k
Z8FRrRjsnMi8y4nMRk5kqlYMdk5MPuTEZC8nJp9yYnKSE5MvOTE5y4lJ1Yph
zonJt5yYfM+JSdWKe0rO+qNacU/J+VtSLecCpyrxOi/nAqcqccHOucDd5Pwt
qZFzjWvmXN1aOVe3ds7fjzo5F7huzgWul3OB6+f8FWmQ81ekac5fkWY5f0Va
5/wV6T3neqcq8cIu53qnKnGm51zvfgr6p1bQP/WC/rks6J+rgv65Luifm4L+
aRQccc2C/mkV9E+7oH86Bf3TL+ifQUH/TAv6Z1bQP8uC/lkV9M+6oH/eC/rn
o6B/Pgv656ugf74L+uen2CRcii3CpdgmXIod8rDYJQ+LPYKmOCRoiiOCpjgj
aIoaQVPcEDRFg6ApWgRN0SZoig5BU3QJmqJHuBR9wqUYkIfFkDwsRuRhMSYP
iwl5WEzJw4LbXL3gNndZ8CeRq4I/iVwX3OxuCm52twV3umbBba5dcJu7L7jH
dQtucI8Fd7dhwd1tVHB3ey64tc0Lbm2LglvbuuDW9lpwrfwouFZ+Fvy546vg
zx3fBVfMn4Ir5i+eI3uO7Tmx59SeM3vO7ak3C8auherGqlurmlbdW9Ud4nm0
Z2jPyJ6pPc/2zO1Z2LO0Z2XP2p7Xf54Le2r21O25tOfKnmt77goiQV3EfNnT
sufBnp49T/ZM7HmxZ2bP0p6VPW/2vNvzYc+nPV/2fBecX+qfbarE+aX+2aVK
nF/qn32qRIupf46pEm3VKmgrdZHaqlPQVqqS2kq9pLYaFLSVukhtJY/aSv3z
SJVoK/XPiCpxfql/JlSJFlP/PFOlv56vTc/Xludr2/O14/na9XwdeL4OPV8n
nq9Tz9eF5+va83Xn+Wp5vh48X+TPnK4eL+hqzdeT52vg+Rp6vkaer7Hna+L5
4vySZ8uebXt27Nm1Z8+eQ3uO7Dm158weLuEFbd4raHOpGla1repYxZW7oM3l
GdgztGdkz9ieiT28GSjJn4uS/KmV5E+9JH8uS/LnqiR/rkvy564kfxolK3az
JH9aJfnzUJI/vZL8eSrJn0lJ/ryU5M+iJH+WJfmzKsmft5L8eS/Jn4+S/Pks
yZ+vkvz5LhXPF7VS8Vyrl4rn+mWpeL68KhXPV9el4vn6plQF7xqlKtholqpX
q12qXg+dUvXqdEtVqtcvVamnQalKjSelKjWZlqrUy6zUJrRclarXal2qXm/v
per1/lHqKX58lkrMz69Sifn1XaqC3z8l/VMv6Z/Lkv65Kumf65L+uSnpn9uS
/mmWrPmtkv5pl/TPfUn/dEv657Gkf4Yl/fNc0j/zkv5ZlPTPsqR/Xkv656Ok
fz5L+uerpH++S/rnp6R/fkveUcvD1aJkqZeHq0XJUi8PV8GSy1mzZJ2XhEtg
yYWsW7LI90sWeXm4ZpQs8qOSS5hUXDBK1vlFyfVLHq4WJUu9PFwtSpZ6ebha
lCz1vxvkT22D/KlvkD+XG+TP1Qb5c71B/txskD+NDfKnuUEetjbIn/YG+dPZ
IH/6G+TPYIP8mW6QP7MN8me+Qf6sNsif9Qb5875B/nxskD+fG+TP1wb5871B
/vz8H1C+PHk=
"]}, CompressedData["
1:eJztwUENACAMBLCbFBIUIWEGsDhpyODTdvU9XUlmJwUAAAAAAAAAAPDJAzWg
J0w=
"]}]], 1]},
ArrayPlot[ReplacePart[template0 - 1,
Catenate[MapIndexed[Thread[#1 -> (#2[[1]] + 1)] &,
DeleteCases[Times[Position[template0, 0], #],
{0, 0}] & /@ res1[[All, 13 ;; -1]]]]],
ColorRules -> {0 -> Black, x_ :> Hue[x/5]},
ImageSize -> 300]]](https://www.wolframcloud.com/obj/resourcesystem/images/8af/8af3735d-76fd-44a4-979c-0e02c18aea78/4dce76a3ff09d1b5.png)

![With[{tetrisData = {SparseArray[
Automatic, {1, 4}, 0, {1, {{0, 4}, {{1}, {2}, {3}, {4}}}, {1, 1, 1, 1}}], SparseArray[
Automatic, {21, 8}, 0, {1, {{0, 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56,
60, 64, 68, 72, 76, 80, 84}, {{5}, {6}, {7}, {8}, {4}, {6}, {
7}, {8}, {3}, {5}, {7}, {8}, {4}, {5}, {6}, {8}, {3}, {5}, {
6}, {8}, {4}, {5}, {6}, {7}, {3}, {4}, {6}, {8}, {3}, {5}, {
6}, {7}, {2}, {4}, {6}, {8}, {3}, {4}, {5}, {7}, {3}, {4}, {
5}, {6}, {2}, {4}, {5}, {6}, {1}, {3}, {5}, {7}, {1}, {3}, {
5}, {6}, {2}, {3}, {4}, {6}, {1}, {3}, {4}, {6}, {2}, {3}, {
4}, {5}, {1}, {2}, {4}, {6}, {1}, {3}, {4}, {5}, {1}, {2}, {
3}, {5}, {1}, {2}, {3}, {4}}}, {1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1}}], SparseArray[
Automatic, {65, 12}, 0, {1, {{0, 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56,
60, 64, 68, 72, 76, 80, 84, 88, 92, 96, 100, 104, 108, 112, 116, 120, 124, 128, 132, 136, 140, 144, 148, 152, 156, 160, 164, 168, 172, 176, 180, 184, 188, 192, 196, 200, 204, 208, 212, 216, 220, 224, 228, 232, 236, 240, 244, 248, 252, 256, 260}, {{9}, {10}, {11}, {12}, {8}, {10}, {11}, {12}, {7}, {
10}, {11}, {12}, {8}, {9}, {11}, {12}, {6}, {9}, {11}, {12}, {
7}, {8}, {11}, {12}, {8}, {9}, {10}, {11}, {5}, {8}, {11}, {
12}, {7}, {8}, {9}, {12}, {7}, {8}, {10}, {11}, {6}, {8}, {
9}, {12}, {7}, {8}, {9}, {11}, {5}, {8}, {9}, {12}, {5}, {8}, {
10}, {11}, {6}, {8}, {9}, {11}, {7}, {8}, {9}, {10}, {5}, {
8}, {9}, {11}, {4}, {7}, {10}, {11}, {5}, {6}, {9}, {12}, {
5}, {7}, {8}, {11}, {3}, {6}, {9}, {12}, {4}, {7}, {8}, {11}, {
5}, {6}, {8}, {11}, {5}, {7}, {8}, {10}, {6}, {7}, {8}, {9}, {
4}, {7}, {8}, {10}, {5}, {7}, {8}, {9}, {4}, {5}, {8}, {11}, {
4}, {7}, {8}, {9}, {5}, {6}, {8}, {9}, {2}, {5}, {8}, {11}, {
3}, {6}, {8}, {9}, {4}, {5}, {7}, {10}, {4}, {5}, {8}, {9}, {
5}, {6}, {7}, {8}, {2}, {5}, {8}, {9}, {4}, {5}, {6}, {9}, {
4}, {5}, {7}, {8}, {3}, {5}, {6}, {9}, {4}, {5}, {6}, {8}, {
1}, {4}, {7}, {10}, {2}, {5}, {6}, {9}, {2}, {5}, {7}, {8}, {
3}, {5}, {6}, {8}, {4}, {5}, {6}, {7}, {2}, {5}, {6}, {8}, {
1}, {4}, {7}, {8}, {2}, {3}, {6}, {9}, {2}, {4}, {5}, {8}, {
1}, {4}, {5}, {8}, {2}, {3}, {5}, {8}, {2}, {4}, {5}, {7}, {
3}, {4}, {5}, {6}, {1}, {4}, {5}, {7}, {2}, {4}, {5}, {6}, {
1}, {2}, {5}, {8}, {1}, {4}, {5}, {6}, {2}, {3}, {5}, {6}, {
1}, {2}, {4}, {7}, {1}, {2}, {5}, {6}, {2}, {3}, {4}, {5}, {
1}, {2}, {3}, {6}, {1}, {2}, {4}, {5}, {1}, {2}, {3}, {5}, {
1}, {2}, {3}, {4}}}, {1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1}}], SparseArray[
Automatic, {113, 16}, 0, {1, {CompressedData["
1:eJwl0BFzwgEAxuH/7oIgCIIgaHdBEARBEARBEHS7IAi6XRB0rdsFQRAEQRAE
QRAEQRAEQRAEg8FgMBgMBoNBMBgM9uz23j0f4P1d397ddK+CILgP/hciTIQo
MeIkSJIiTYYsOfIUKFKiTIUqNeo0aNKiTYcefQYMGTFmwpQZcxYsWbFmw5Yd
ew4cOXHmgUeeeOaFV95454NPLnzxzc/feSFChIkQJUacBElSpMmQJUeeAkVK
lKlQpUadBk1atOnQo8+AISPGTJgyY86CJSvWbNiyY8+BIyfO/AJZhzT8
"], CompressedData["
1:eJwljo0RgzAIhWMSgQSMrtCVOoILdMkO1g975zveH8HX/XnftZTy3UrhK8c6
rwAOZs4AmNPRTCc0vPF469T0Pa4xUwc4luIbHhoeF/wcLMvMfnJPoOlaXPrX
hzDhCx77yL6T+2no/u+FcFA4Jk+HycN0kh+icynLLTscInNluWfOcTpOJ3P0
oG9R05f0DYzZyDs+Gm4Bd7qTHnvJ1Td+jolHnx9reOhRmfAJNzrkSq7e0fhW
OVw5Vp+cycPkyUdtMhuLdAxfG0sbR7fHS77T6YaH7mAXpuCDRt5y7qD/AFjI
EXE=
"]}, CompressedData["
1:eJxTTMoPSmJkYGA4AiQYR8GQBwDtgQQx
"]}], SparseArray[Automatic, {161, 20}, 0, {1, {CompressedData["
1:eJwl0hFzAgAABeC2C4IgCIKg3QVBEARBEARB0O2CIOh2QdBtQRAEQRAEwWAQ
dLtgMAiCIBgMBkEQBMFgEAyCwSDY1+3dfT/gvXs3dw+391eBQOA58J8gIcJE
iBIjToIkKdJkyJIjT4EiJcpUqFKjToMmLdp06NKjz4AhI8ZMeOSJKTPmvPDK
giUr1rzxzgcbtuzYc+CTL458c+KHX86X8oYIEiJMhCgx4iRIkiJNhiw58hQo
UqJMhSo16jRo0qJNhy49+gwYMmLMhEeemDJjzguvLFiyYs0b73ywYcuOPQc+
+eLINyd++OV8OcG1/oQIEyFKjDgJkqRIkyFLjjwFipQoU6FKjToNmrRo06FL
jz4DhvwBPY9Kng==
"], CompressedData["
1:eJwlj9d5wzAMhMUmAiygihfwShnBC2SJDJ4f1gN1hyv4oPfn9+cTt2374xPA
87pfi2e8yTsQbDGDkzccjZlQQ58EJ6HBU/TufHpm4Z0XeCuZMb/8auiCryD8
7sPzhn+caKBdQrazEH4qXiUjoLb1Ysab3lny8LOS1WZ3Q2M+BJ/cKuR3DqrM
wnHopzwZq86VHEeozxyCb5ncDq8ciXaQM7pLWY5+FPJVhndNWERmJrL01s6h
u2vinbaExSA76dZ+0PN5FrxIlh5eW8z43lOrLEUDlb1j0hvwkfECP0MPXS3z
c2j44r2WHj4i+VzUChpzT/jkGl08mYlD0UZ6fI3OMxmOyD5zCL4GMHIgcyej
9FouX73HVL2jiQX4EjgqOE+eKy2xCNQQd8869wx+1kgJZP5iDZTAAjrfefkf
0A8cmg==
"]}, CompressedData["
1:eJxTTMoPSmJkYGBoYWJgYBwFo2CAAQC7VQSy
"]}], SparseArray[Automatic, {209, 24}, 0, {1, {CompressedData["
1:eJwl0pGTIgAYxuHubiEIgiAIupkgCIIgCIIgCHZugiBoboKg2QuCIAiCIAiC
YCEIgoUgCIIgCILmZiEIgmBhIQiC4J6d+2aeP+D3zvfz959fL98CgcDfwP97
IkiIMBGixIiTIEmKNBmy5MhToEiJZ8pUqFKjToMmLdp06NKjz4AhI8ZMeGXK
jDlvLFiyYs2GLTv2HHjnyIkzFz745MqNO4+veEM8ESREmAhRYsRJkCRFmgxZ
cuQpUKTEM2UqVKlRp0GTFm06dOnRZ8CQEWMmvDJlxpw3FixZsWbDlh17Drxz
5MSZCx98cuXGncfXE3zXT5AQYSJEiREnQZIUaTJkyZGnQJESz5SpUKVGnQZN
WrTp0KVHnwFDRoyZ8MqUGXPeWLBkxZoNW3bsOfDOkRNnLnzwyZUbdx4Efugn
SIgwEaLEiJMgSYo0GbLkyFPgH5PFZGA=
"], CompressedData["
1:eJwlkEl2xCAMRG0GM4jRbtu9zV1yghwhF8j9d/lqL3ggUb9K8PX79/NrlmX5
tsuysp/X/d5Zk/WiGHrWnTX3+33Q7FpP+giH1qwBULhvWg+9Py9B0wHG3N+N
vQ/V7begrU//al31rzPDFHQdY2HnfLeuzLzyUK/95nxWAhqmCU7QNsKyMugq
IdTK7Kmr57ykkE1AhMtopcy7cF8JTsqil6dWdsam3uPMDJ+f/rHhERg4wWTB
46ODh4GfeKpu0HslHgI/vfIMLYRFhk4ZFk3gTH3ADrzmBkvviDwIfjjlCc6E
4LHHBIt55iFwHR+4gv+YgUeF525Y5QlOhOAxN/Qh1iMxhOdMPfGCFzLUu0zO
3agHwZEQPIZHHxnAKYcWj0atXLFJvWV4PoReW/kU+O7Q+03mhiYwhFUexj+1
8mKi+ufueJR7+hW+WfTOw380sOhhBT/VZHrN8iBYgS2eEMPA1sFxv3KmrnAZ
H6GuhofAZTgYPCx6zByDo02waDdZGX59+mhUH9NqQrUEwaDz9Dy9mAwGBkPu
dde7jT2ugCztefbAcv9nYSrD
"]}, CompressedData["
1:eJxTTMoPSmJkYGBwYWZgYBwFo2AUUAQAuqkFMw==
"]}], SparseArray[Automatic, {257, 28}, 0, {1, {CompressedData["
1:eJwl0xGQIgAUBuDudiEIgoUg6GaCIAiChSAIgqC5CYKguQmC5i5YWAiCIAiC
IAiCIFhYCIIgCIIgCIIgCIIgCILgvr17M9/z/5/3fvz68/P3t0Ag8P1rmWeC
hAjzQoQoMeIkSJIizSsZsuTIU6BIiTIVqtSo06DJG++0aNOhS48+A4aMGDNh
ygefzJizYMmKNRu27Nhz4MiJMxeu3Ljz+Aqvg2eChAjzQoQoMeIkSJIizSsZ
suTIU6BIiTIVqtSo06DJG++0aNOhS48+A4aMGDNhygefzJizYMmKNRu27Nhz
4MiJMxeu3Ljz+HcE8hMkRJgXIkSJESdBkhRpXsmQJUeeAkVKlKlQpUadBk3e
eKdFmw5devQZMGTEmAlTPvhkxpwFS1as2bBlx54DR06cuXDlxp0HgSf5CRIi
zAsRosSIkyBJijSvZMiSI0+BIiXKVKhSo06DJm+806JNhy49+gwYMmLMhCkf
fDJjzoIlK9Zs2LJjz4EjJ85cuHLjzuPp//M/8xdv+IFD
"], CompressedData["
1:eJwl0Et24zAMRFHrb4nUl5KT2Jn0lnoJ2UD2P+sL94AHRBH1APDPz+/fn/p2
u7Xt7VaJX8/X9+V8upxicU73D0IRj9Av+unQTsUPj4f7HjVMi/eD8aAX5l2c
1W9RV6Lm4r9es9odcAc4StRez809867ifkT9+VrUi8/MO7vLX5tm+xG+E/t6
JZxtD095zjziV+LP7vLnqvmmET08F/05YczL9b1quhkk84qfE05yl3vXXz09
vGcKTT7iZUvhXKthEr/4MeCNeJOcpsY8fN4eGGUKTX63YLIo3qnHNWH0eKPo
7s08Fss88/L2H2PowbAsTsE+R4t1OAPG3V3+mJJ5DJZ4sub30Nzxr9HSOAc+
/3I5Z4vXB2vaPrDLpFnK4V0K3o5/3i2Ms2PzzufAK5YGr8Pq5TR160OPY0rB
mPV88ws2by49r3jUeC1WJ6cV/H3U2Fv4lu4/++h9KOY2GqzjF/fK5zV4rZym
xjw83sI/t6HJ9dg7S2Mtd0O1GOJW4zXucu9m4qGv/LkJTa7H1loca8ZfGv7a
EelmsVinvh/e3lSHHn7LYmTcubZU5Yhr0+pvkFZtp2EVWviaNzdh8gyLM9fN
uOHkBrjton7IGFNVv3kTlvp+dnJV31eM1LRR2+PFe2eOLqmfahD3eBvUjjWw
Q29D7ytmZ3TutE5s/wFJwzvs
"]}, CompressedData["
1:eJxTTMoPSmJkYGBgYWFgYBwFo2AUjGgAAOt9BbQ=
"]}], SparseArray[Automatic, {305, 32}, 0, {1, {CompressedData["
1:eJwl0xGQIgAUBuDudiEIgiAIupkgCJqbIAiCIAiamyAImpsgaO6CIAiCIAiC
IAiCIAiCIAiCIFhYCBaCIAiChYVg4b6dezPf8/9/8378/vvrz7dAIPDza5ln
goQIEyFKjDgJkqRIkyFLjjwFipQoU6FKjToNmrRo06FLjz4DhowYM2HKjDkL
lqxYs2HLjj0Hjrzwyok3zly4cuPOOx88+PwKr4NngoQIEyFKjDgJkqRIkyFL
jjwFipQoU6FKjToNmrRo06FLjz4DhowYM2HKjDkLlqxYs2HLjj0Hjrzwyok3
zly4cuPOOx88+Py6/3f5CRIiTIQoMeIkSJIiTYYsOfIUKFKiTIUqNeo0aNKi
TYcuPfoMGDJizIQpM+YsWLJizYYtO/YcOPLCKyfeOHPhyo0773zw4JPAk/wE
CREmQpQYcRIkSZEmQ5YceQoUKVGmQpUadRo0adGmQ5cefQYMGTFmwpQZcxYs
WbFmw5Ydew4ceeGVE2+cuXDlxp13Pnjw+fT/+Z8JEiJMhCgx4iRIkiJNhiw5
8hQoUqJMhSo16jRo0qJNhy49+gwYMmLMhCkz5ixYsmLNhi079hz4B6nBlVM=
"], CompressedData["
1:eJwl0VmimzAMQNGEMQFsCGbInNctdQndQDfZhfUQPhxLsn2vUH79+fv7T3Y4
HP4Vh8PR/np/fp5+rvbVWqyHwqq2WLO1Xj8/d8VFfbaW1V0Ppm/8/twczs4n
awZYPB68Sd/89e7dn9xZ1utPsk+gM5j803s/7mfvCTx6nwBnktGeSCZw+Tti
DRiX/fzVi+WfRBzmzXP9TBoYiROh+BUweyzxM9rFzr/vr920+dZ30tBFEyOx
+NnhRZx+0C95EMvdud1x1jZtvuXVD+tnwBk12e/7o8UOeNFHx7127+RqepqX
hkf+jD0+1kWzJ564x/eGo8MLBhH22q2Vqz34Nt58NgC1R4g8mDUX/sJ57TXU
YnYG0n196SG/822sSX7vAj5OxYE7c61RMyf8xiBag2m/nvEuv/Fsjqv81nbY
ONFwSg7siWsJGlFba57GgJr9zsK1edRwNRA0WeDjJp6504jaUnGcMM8GdN7v
zbVcbeWcuPQwrOfmcus0nG8OTbaakc8lT40tniq7eOHcOAOfHvql1Wi28TXX
aEY+FdgVXu1PkKdSLJ95RqyehzvO9alfT1iNpo/+gHqPU85R4lYGVO21sZCr
6S1EviSfqpoD76zpat/HjKPAKw2o3GuXXK6W+DZW4BrVUllx4OFGrqHWTI5V
GEzx9bRJPvJsnE4+FiU2Bl7g6CsNZD4+N5D8y25G+QU7ii95gedtZRhYHXYs
SeV9ZhDZfhZxQ5bjEJWawWgxQ0Emj0cffdzPAmZ3zM6XQgMYXU4gdrfqMLY7
p5zImzYDFLtTtt407tQZsOWs2M6qI4jVWGe10l78B215URQ=
"]}, CompressedData["
1:eJxTTMoPSmJkYGA4wsLAwDgKRsEoGAVDGAAAEWQHNA==
"]}], SparseArray[Automatic, {353, 36}, 0, {1, {CompressedData["
1:eJwl1CGwKQgUBuC7++7OCIIgCIKdEQRBEARBEATB7AiCYN4IgnlPEARBEARB
EARBEARBEARBEIQbbrhBEARBEARBEN53Z8/Md/p/zpzz78/f//366+3t7ed3
U+8ECBIiTIQoMeIkSJIiTYYsOfIUKFKiTIUqNeo0aNKiTYcuPfoMGDJizIQp
M+YsWLJizYYtO/Yc+OCTL46cOHPhyo07D568vsObwTsBgoQIEyFKjDgJkqRI
kyFLjjwFipQoU6FKjToNmrRo06FLjz4DhowYM2HKjDkLlqxYs2HLjj0HPvjk
iyMnzly4cuPOgyev7/3/LT8BgoQIEyFKjDgJkqRIkyFLjjwFipQoU6FKjToN
mrRo06FLjz4DhowYM2HKjDkLlqxYs2HLjj0HPvjkiyMnzly4cuPOgycv3n7I
T4AgIcJEiBIjToIkKdJkyJIjT4EiJcpUqFKjToMmLdp06NKjz4AhI8ZMmDJj
zoIlK9Zs2LJjz4EPPvniyIkzF67cuPPgyevH/8f/ToAgIcJEiBIjToIkKdJk
yJIjT4EiJcpUqFKjToMmLdp06NKjz4AhI8ZMmDJjzoIlK9Zs2LJjz4EPPvni
yIkzF67cuPPgyev78f0jPwGChAgTIUqMOAmSpEiTIUuOPAWKlChToUqNOg2a
tGjToUuPPn8AmeCrhQ==
"], CompressedData["
1:eJwdkdmBozAQRG1ujE5AJ+MTR7QhTAKbxAa+T/rQdHfJqlf0vH///vltLpfL
v/5yuVLfn/P74s9BzZzEeSJktMSJnAdCKtpxfiM1cFLm9zy6cxnLPY8D1XMi
JgmDHy5X3oTyG8w81fLOUQPGMZV3x5dzWt57fh9i1T6O3uCzUz3AEItHPjkf
g5fD3IeqvVc8dmaNp6VnPjdmRxgfimcq+kl9a/ydr9rL4qfwNlT6z04w54tv
5Bvygf6hfyk4u6v60+Al8dVU+rddj+9GyJ1AjqD4Zu5ghKeEY9d8rnhte71/
aLxhHQKWomd+GZYC69gJDCOhw/MPAdNYsuPJfFf4w8wzzAWmZEZ7ahYFM298
AIyI/qS/LzC1iW+DJznI4H4kDJhpgnljSYIZ7aFYHtxElsOulRdE1cNL40mO
LPCHF0d4Cz3zXbJAeJEM2RAUhufuPsOTyj8VPmRIC0uCEwY4sI8bM9qPYJlw
AvykTeGs5e6HmqfClO4h8SRHuUswfQ+TDHlhibA8GaLShWMzJ42FJ/a7IAwZ
ih5nfOG5Dh4Z+P71QMs3FgnPkSNIVTim3GVqHGDelo2MVQ8T/i1M+OzAZmY4
zgtZOJod2BU90YceLhmK7kc8Gziw+X6TmOPEPxG2Wwgp+AD8LXeR3nfwptnm
GT/45d4N+MNbr/zTyMAOdEQLI8uEuS58ACyDDle6FvY48S34Mu89DLiWHOxA
BWY/sESY9sZHwNDonn5vYA6jjiN+5CCD2Dr84Rn4e0vP7HoWCc+QYZ3mylFt
1VUY8INvW7xh6YZKv3csD46GbUfC4S2bqkvf8x6uaVgM/upKpd9aFoevgmeG
sfjO7GHZqLbthOvwgFl00xY/FoSnhKX7oXhOlmOadtlbgLCKpvEWVxaCl4Ch
ur74jIajr80Nbp0VfrLtyruB3NNMRauz5L1oMG2B8duJilZn9I4Mw0gt/XLF
CH2glv6G1lO7/yxFaD0=
"]}, CompressedData["
1:eJxTTMoPSmJkYGBoYWVgYBwFo2AUjIJRMGAAAGSHB7U=
"]}]}},
Length[ResourceFunction["FindExactCover"][Normal[#], All]
] & /@ tetrisData[[1 ;; 5]]]](https://www.wolframcloud.com/obj/resourcesystem/images/8af/8af3735d-76fd-44a4-979c-0e02c18aea78/50a34d5c76103e26.png)
![(* Evaluate this cell to get the example input *) CloudGet["https://www.wolframcloud.com/obj/b2550ade-d752-44cd-b82c-081805b83d47"]](https://www.wolframcloud.com/obj/resourcesystem/images/8af/8af3735d-76fd-44a4-979c-0e02c18aea78/61b1d1aef3997fd1.png)