Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Try to find a counterexample to an equational hypothesis in a given system of axioms
ResourceFunction["FindEquationalCounterexample"][hyp,axms] tries to find an equational counterexample to the symbolic hypotheses hyp using the axioms axms. |
| expr1⩵expr2 | assertion of equality |
| ForAll[vars,stmt] | assertion that stmt is true for all values of vars |
Find a counterexample to an elementary hypothesis in group theory:
| In[1]:= |
|
| Out[1]= |
|
Show the counterexample association:
| In[2]:= |
|
| Out[2]= |
|
Generate a function to verify that this is a valid counterexample to the hypothesis:
| In[3]:= |
|
| Out[3]= |
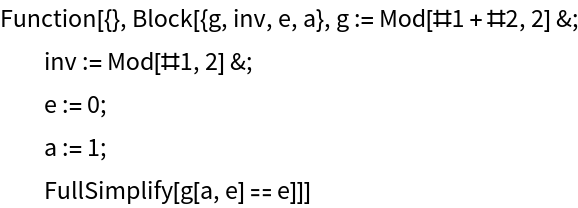
|
| In[4]:= |
|
| Out[4]= |
|
Generate a function to verify that this counterexample is consistent with the underlying axioms:
| In[5]:= |
|
| Out[5]= |

|
| In[6]:= |
|
| Out[6]= |
|
Find a counterexample to a more sophisticated hypothesis in group theory:
| In[7]:= |
|
| Out[7]= |
|
Show the counterexample association:
| In[8]:= |
|
| Out[8]= |
|
Generate a function to verify that this is a valid counterexample to the hypothesis:
| In[9]:= |
|
| Out[9]= |
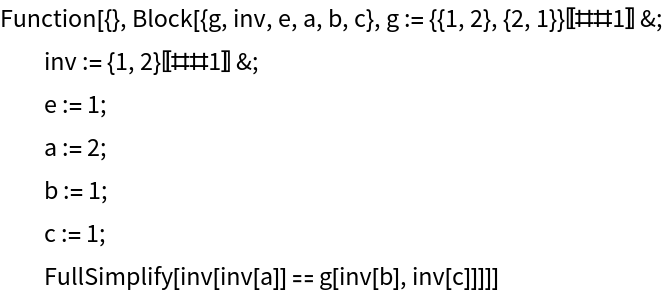
|
| In[10]:= |
|
| Out[10]= |
|
Generate a function to verify that this counterexample is consistent with the underlying axioms:
| In[11]:= |
|
| Out[11]= |

|
| In[12]:= |
|
| Out[12]= |
|
FindEquationalCounterexample supports hypotheses formulated in any equational axiom system, including Wolfram's shortest possible axiom for Boolean algebra (finding a counterexample to the hypothesis that the Nand operator is associative):
| In[13]:= |
![counterexample = ResourceFunction["FindEquationalCounterexample"][
ForAll[{a, b, c}, nand[nand[a, b], c] == nand[a, nand[b, c]]], ForAll[{a, b, c}, nand[nand[nand[a, b], c], nand[a, nand[nand[a, c], a]]] == c]]](https://www.wolframcloud.com/obj/resourcesystem/images/eaf/eafbc16b-a639-4c04-815d-d9f3c3afb63b/14121efeb47d747a.png)
|
| Out[13]= |
|
Show the counterexample association:
| In[14]:= |
|
| Out[14]= |
|
Generate a function to verify that this is a valid counterexample to the hypothesis:
| In[15]:= |
|
| Out[15]= |
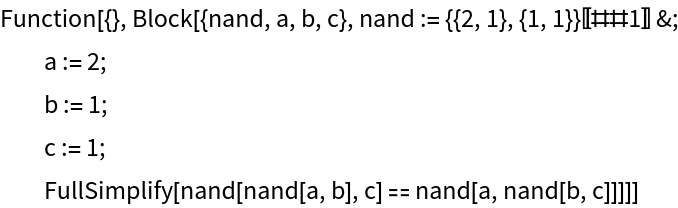
|
| In[16]:= |
|
| Out[16]= |
|
Generate a function to verify that this counterexample is consistent with the underlying axioms:
| In[17]:= |
|
| Out[17]= |

|
| In[18]:= |
|
| Out[18]= |
|
Ring theory (finding a counterexample to the hypothesis that every ring is commutative):
| In[19]:= |
![counterexample = ResourceFunction["FindEquationalCounterexample"][
ForAll[{a, b}, f[a, b] == f[b, a]], {ForAll[{a, b, c}, g[a, g[b, c]] == g[g[a, b], c]], ForAll[a, g[a, e] == a], ForAll[a, g[a, inv[a]] == e], ForAll[{a, b}, g[a, b] == g[b, a]], ForAll[{a, b, c}, f[a, f[b, c]] == f[f[a, b], c]], ForAll[{a, b, c}, f[a, g[b, c]] == g[f[a, b], f[a, c]]]}]](https://www.wolframcloud.com/obj/resourcesystem/images/eaf/eafbc16b-a639-4c04-815d-d9f3c3afb63b/2370b84700d3bbac.png)
|
| Out[19]= |
|
Show the counterexample association:
| In[20]:= |
|
| Out[20]= |
|
Generate a function to verify that this is a valid counterexample to the hypothesis:
| In[21]:= |
|
| Out[21]= |

|
| In[22]:= |
|
| Out[22]= |
|
Generate a function to verify that this counterexample is consistent with the underlying axioms:
| In[23]:= |
|
| Out[23]= |

|
| In[24]:= |
|
| Out[24]= |
|
Equational Presburger arithmetic (finding a counterexample to the hypothesis that every integer is equal to its negation):
| In[25]:= |
![counterexample = ResourceFunction["FindEquationalCounterexample"][
ForAll[x, neg[x] == x], {ForAll[x, plus[x, zero] == x], ForAll[x, plus[x, neg[x]] == zero], ForAll[{x, y, z}, plus[plus[x, y], z] == plus[x, plus[y, z]]]}]](https://www.wolframcloud.com/obj/resourcesystem/images/eaf/eafbc16b-a639-4c04-815d-d9f3c3afb63b/33a6fad8d8c0cfb1.png)
|
| Out[25]= |
|
Show the counterexample association:
| In[26]:= |
|
| Out[26]= |
|
Generate a function to verify that this is a valid counterexample to the hypothesis:
| In[27]:= |
|
| Out[27]= |
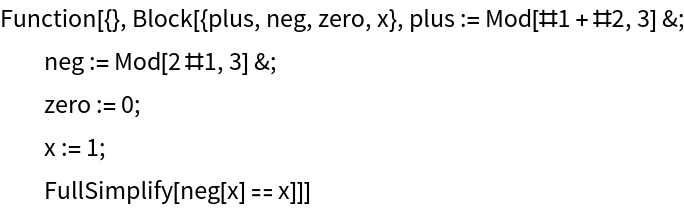
|
| In[28]:= |
|
| Out[28]= |
|
Generate a function to verify that this counterexample is consistent with the underlying axioms:
| In[29]:= |
|
| Out[29]= |

|
| In[30]:= |
|
| Out[30]= |
|
Find a counterexample from a list of axioms:
| In[31]:= |
|
| Out[31]= |
|
Express the axioms as a conjunction:
| In[32]:= |
|
| Out[32]= |
|
Find a counterexample to a list of hypotheses:
| In[33]:= |
![counterexample = ResourceFunction[
"FindEquationalCounterexample"][{ForAll[a, g[a, e] == e], ForAll[{b, c, d}, inv[inv[b]] == g[inv[c], inv[d]]]}, {ForAll[{a, b, c}, g[a, g[b, c]] == g[g[a, b], c]], ForAll[a, g[a, e] == a], ForAll[a, g[a, inv[a]] == e]}]](https://www.wolframcloud.com/obj/resourcesystem/images/eaf/eafbc16b-a639-4c04-815d-d9f3c3afb63b/190336799e640ab2.png)
|
| Out[33]= |
|
| In[34]:= |
|
| Out[34]= |
|
Express the hypotheses as a conjunction:
| In[35]:= |
![ResourceFunction["FindEquationalCounterexample"][
ForAll[a, g[a, e] == e] && ForAll[{b, c, d}, inv[inv[b]] == g[inv[c], inv[d]]], {ForAll[{a, b, c}, g[a, g[b, c]] == g[g[a, b], c]], ForAll[a, g[a, e] == a], ForAll[a, g[a, inv[a]] == e]}]](https://www.wolframcloud.com/obj/resourcesystem/images/eaf/eafbc16b-a639-4c04-815d-d9f3c3afb63b/457d35cd1028872d.png)
|
| Out[35]= |
|
This work is licensed under a Creative Commons Attribution 4.0 International License