Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Find an instance of n-dimensional vectors that produce a specified distance matrix
ResourceFunction["FindDistanceInstance"][mat,n] finds an instance of n-dimensional vectors that will generate the specified distance matrix mat. |
Find a set of three 2D points that are equidistant:
| In[1]:= | ![pts = ResourceFunction["FindDistanceInstance"][({
{0, 1, 1},
{1, 0, 1},
{1, 1, 0}
}), 2]](https://www.wolframcloud.com/obj/resourcesystem/images/e3d/e3daa261-71a8-4e5a-9c4c-aee7a97ab6a7/0186fe75b59f588f.png) |
| Out[1]= |
Verify that the points produce the specified distance matrix:
| In[2]:= |
| Out[2]= |
Find a set of four 3D points that are equidistant:
| In[3]:= |
| Out[3]= |
Verify that the points are equidistant:
| In[4]:= |
| Out[4]= |
The points form a regular tetrahedron in 3D:
| In[5]:= |
| Out[5]= | 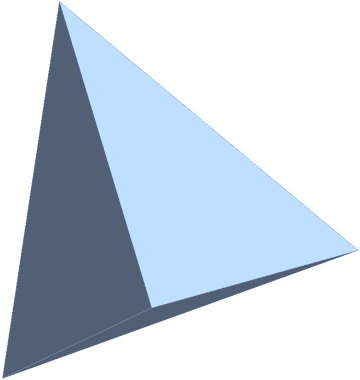 |
A 4D Hilbert matrix with its diagonal zeroed cannot be a distance matrix because it fails to satisfy some triangle inequalities:
| In[6]:= |
| Out[7]= |
Use a larger tolerance to get a result anyway:
| In[8]:= |
| Out[8]= |
Find a set of three 2D points whose distances form a HilbertMatrix:
| In[9]:= |
| Out[10]= |
| In[11]:= |
| Out[11]= | 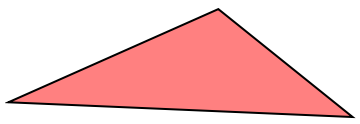 |
Find a set of three 2D points whose distances form a Toeplitz matrix:
| In[12]:= |
| Out[12]= |
| In[13]:= |
| Out[13]= | 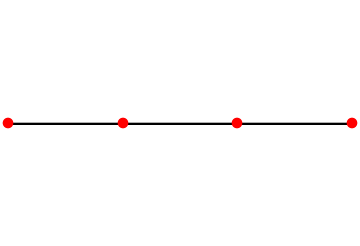 |
This work is licensed under a Creative Commons Attribution 4.0 International License