Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Attempt to find a proof of a theorem in combinatory logic using a given combinatory calculus
ResourceFunction["FindCombinatorProof"][thm,<|"Combinators"→comb,"Rules"→rules|>] tries to find an equational proof of the combinatory logic theorem thm using the combinators comb and reduction rules rules. | |
ResourceFunction["FindCombinatorProof"][thm,calc] tries to find an equational proof of the combinatory logic theorem thm using the named combinatory calculus calc. |
| TimeConstraint | Infinity | how much time to allow |
Prove an elementary theorem about the single-variable fixed-point (y) combinator, with the reduction rule explicitly specified:
| In[1]:= |
|
| Out[1]= |
|
Show the abstract proof network, with tooltips showing the intermediate expressions:
| In[2]:= |
|
| Out[2]= |
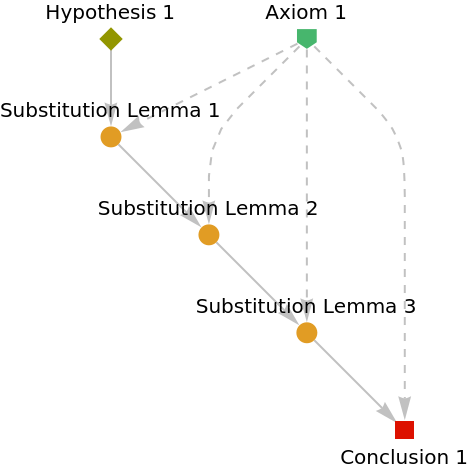
|
Show the complete list of proof steps as a Dataset object:
| In[3]:= |
|
| Out[3]= |
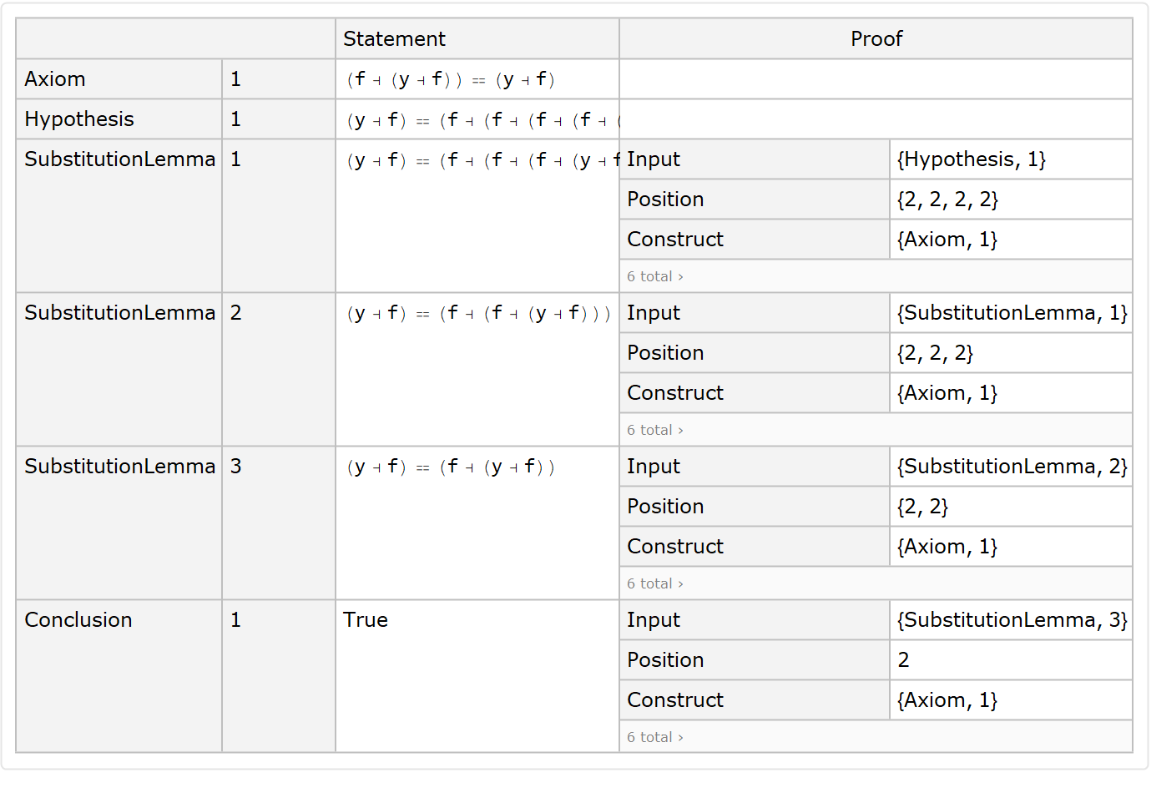
|
Typeset a natural language argument:
| In[4]:= |
|
| Out[4]= |
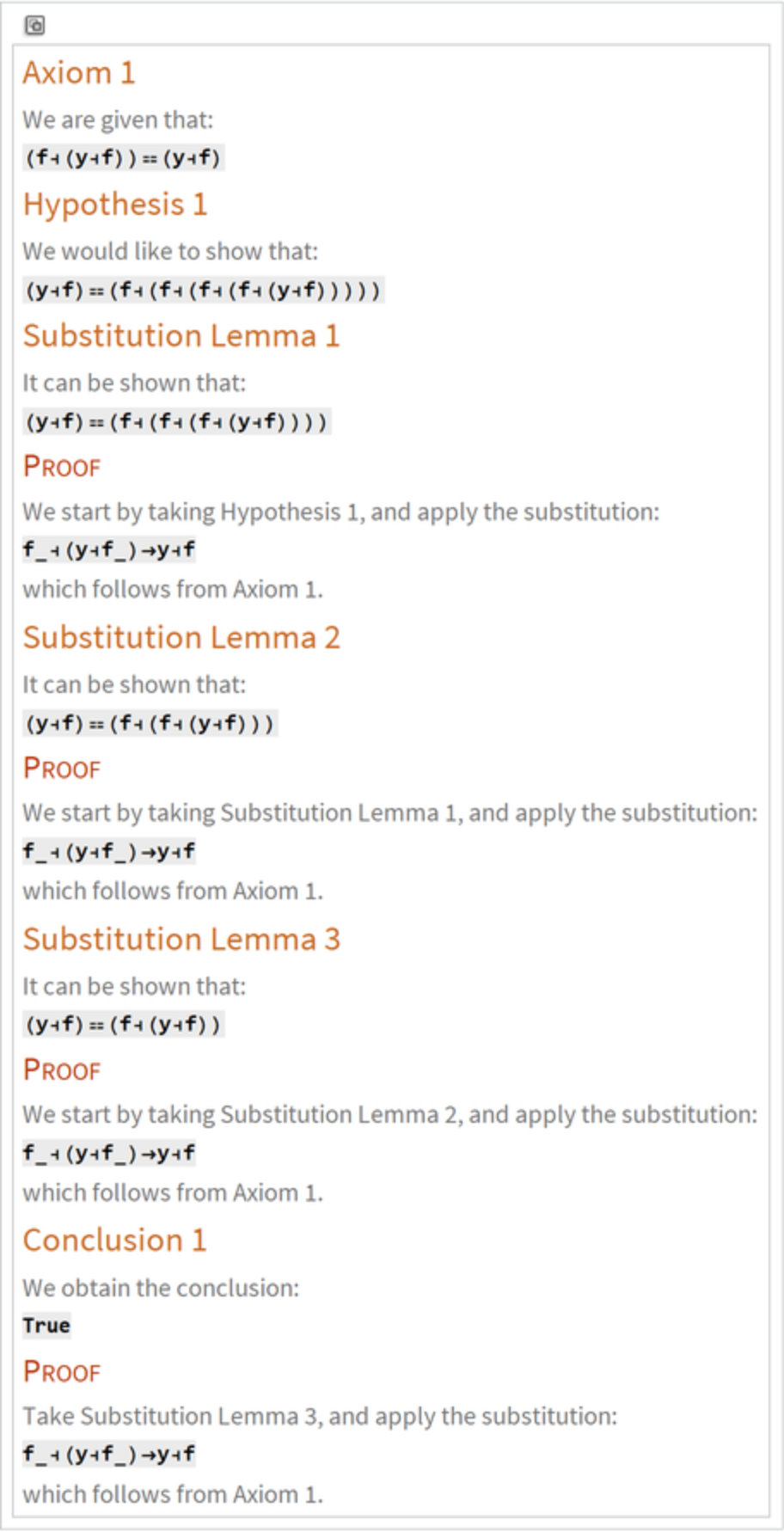
|
Prove a more sophisticated theorem involving the S-K combinatory calculus:
| In[5]:= |
![proof = ResourceFunction["FindCombinatorProof"][
s[s[s[s]]][s][s][k] == s[k[s[s][s[s[s]]][k]]][
k[k[s[s][s[s[s]]][k]]][
s[s][k[s[k][s[s[s]][k]]]][k[k[s[k][s[s[s]][k]]]]]]], <|
"Combinators" -> {s, k}, "Rules" -> {s[x][y][z] == x[z][y[z]], k[x][y] == x}|>]](https://www.wolframcloud.com/obj/resourcesystem/images/b7e/b7e9f2ca-b42c-48a0-bc14-88b3bc57ace3/520be12bd8539858.png)
|
| Out[5]= |
|
Show the abstract proof network:
| In[6]:= |
|
| Out[6]= |
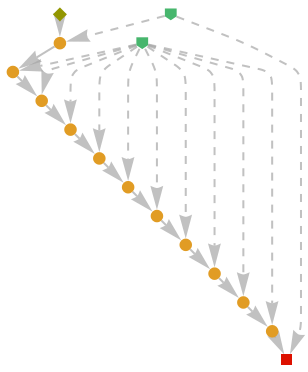
|
Prove a theorem using one of FindCombinatorProof's built-in combinatory calculi (Schönfinkel's B-C-I calculus):
| In[7]:= |
|
| Out[7]= |
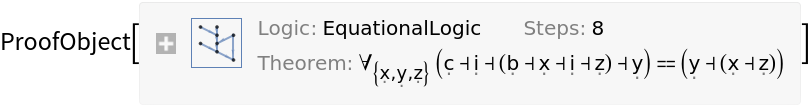
|
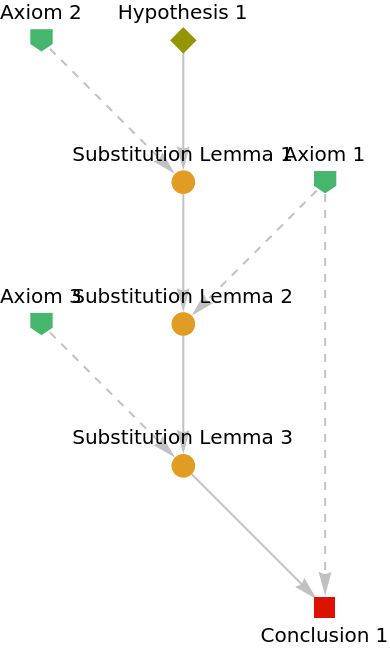
Show the abstract proof network:
| In[8]:= |
|
| Out[8]= |
|
Show that a combinator equivalence proposition cannot be derived from a given combinatory calculus:
| In[9]:= |
|
| Out[9]= |
|
FindCombinatorProof supports a variety of named combinatory calculi, including the single-variable fixed-point (y) combinator:
| In[10]:= |
|
| Out[10]= |
|
The two-variable fixed-point (y) combinator:
| In[11]:= |
|
| Out[11]= |
|
The S-K calculus:
| In[12]:= |
|
| Out[12]= |
|
The S-K-I calculus:
| In[13]:= |
|
| Out[13]= |
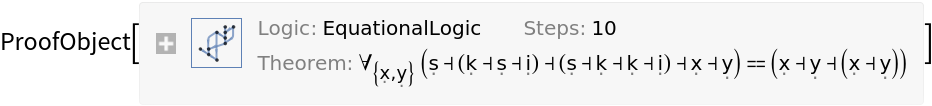
|
Schönfinkel's B and C combinators:
| In[14]:= |
|
| Out[14]= |

|
The B-C-I calculus:
| In[15]:= |
|
| Out[15]= |
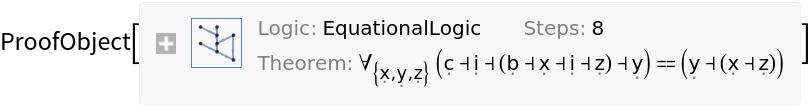
|
FindCombinatorProof accepts both individual theorems and lists of theorems:
| In[16]:= |
|
| Out[16]= |
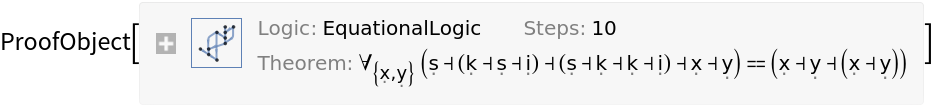
|
| In[17]:= |
![ResourceFunction[
"FindCombinatorProof"][{\[FormalS][\[FormalK][\[FormalS]][\[FormalI]]][\[FormalS][\[FormalK]][\[FormalK]][\[FormalI]]][\[FormalX]][\[FormalY]] == \[FormalX][\[FormalY]][\[FormalX][\[FormalY]]], \[FormalS][\[FormalK][\[FormalS]][\[FormalI]]][\[FormalS][\[FormalK]][\[FormalK]][\[FormalI]]][\[FormalY]][\[FormalX]] == \[FormalY][\[FormalX]][\[FormalY][\[FormalX]]]}, "SKI"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7e/b7e9f2ca-b42c-48a0-bc14-88b3bc57ace3/2316ef23a980b83a.png)
|
| Out[17]= |

|
Use TimeConstraint→t to limit the computation time to t seconds:
| In[18]:= |
![ResourceFunction[
"FindCombinatorProof"][\[FormalS][\[FormalS][\[FormalS][\[FormalS]]]][\[FormalS]][\[FormalS]][\[FormalK]] == \[FormalS][\[FormalK][\[FormalS][\[FormalS]][\[FormalS][\[FormalS][\[FormalS]]]][\[FormalK]]]][\[FormalK][\[FormalK][\[FormalS][\[FormalS]][\[FormalS][\[FormalS][\[FormalS]]]][\[FormalK]]]][\[FormalS][\[FormalS]][\[FormalK][\[FormalS][\[FormalK]][\[FormalS][\[FormalS][\[FormalS]]][\[FormalK]]]]][\[FormalK][\[FormalK][\[FormalS][\[FormalK]][\[FormalS][\[FormalS][\[FormalS]]][\[FormalK]]]]]]]], "SK", TimeConstraint -> 0.001]](https://www.wolframcloud.com/obj/resourcesystem/images/b7e/b7e9f2ca-b42c-48a0-bc14-88b3bc57ace3/5619b77273f081ff.png)
|
| Out[18]= |
|
| In[19]:= |
![ResourceFunction[
"FindCombinatorProof"][\[FormalS][\[FormalS][\[FormalS][\[FormalS]]]][\[FormalS]][\[FormalS]][\[FormalK]] == \[FormalS][\[FormalK][\[FormalS][\[FormalS]][\[FormalS][\[FormalS][\[FormalS]]]][\[FormalK]]]][\[FormalK][\[FormalK][\[FormalS][\[FormalS]][\[FormalS][\[FormalS][\[FormalS]]]][\[FormalK]]]][\[FormalS][\[FormalS]][\[FormalK][\[FormalS][\[FormalK]][\[FormalS][\[FormalS][\[FormalS]]][\[FormalK]]]]][\[FormalK][\[FormalK][\[FormalS][\[FormalK]][\[FormalS][\[FormalS][\[FormalS]]][\[FormalK]]]]]]]], "SK"] // AbsoluteTiming](https://www.wolframcloud.com/obj/resourcesystem/images/b7e/b7e9f2ca-b42c-48a0-bc14-88b3bc57ace3/2e52caae3695bf38.png)
|
| Out[19]= |

|
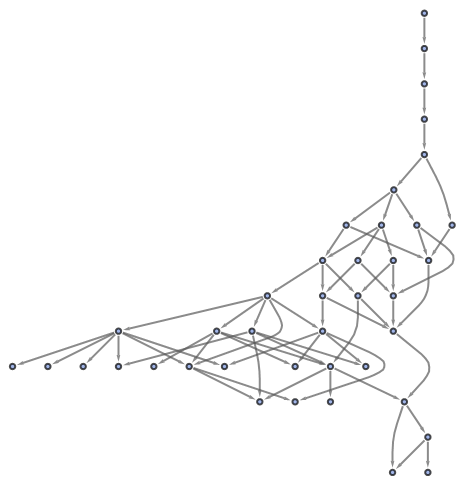
FindCombinatorProof will return a proof object for a particular theorem if and only if the associated path exists in the corresponding multiway system:
| In[20]:= |
![ResourceFunction[
"FindCombinatorProof"][\[FormalS][\[FormalS][\[FormalS][\[FormalS]]]][\[FormalS]][\[FormalS]][\[FormalK]] == \[FormalS][\[FormalK][\[FormalS][\[FormalS]][\[FormalS][\[FormalS][\[FormalS]]]][\[FormalK]]]][\[FormalK][\[FormalK][\[FormalS][\[FormalS]][\[FormalS][\[FormalS][\[FormalS]]]][\[FormalK]]]][\[FormalS][\[FormalS]][\[FormalK][\[FormalS][\[FormalK]][\[FormalS][\[FormalS][\[FormalS]]][\[FormalK]]]]][\[FormalK][\[FormalK][\[FormalS][\[FormalK]][\[FormalS][\[FormalS][\[FormalS]]][\[FormalK]]]]]]]], "SK"]](https://www.wolframcloud.com/obj/resourcesystem/images/b7e/b7e9f2ca-b42c-48a0-bc14-88b3bc57ace3/1f2b11f8cb809ee6.png)
|
| Out[20]= |
|
| In[21]:= |
|
| Out[21]= |
|
| In[22]:= |
|
| Out[22]= |
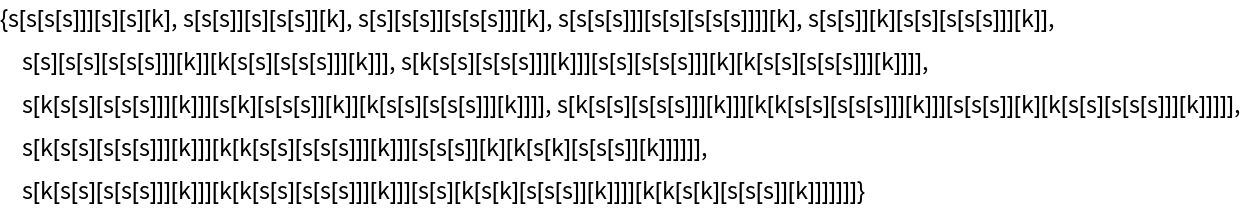
|
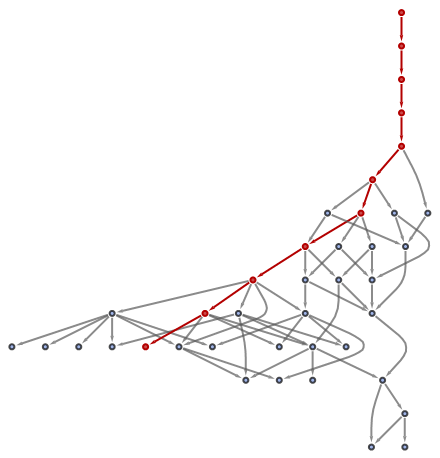
| In[23]:= |
|
| Out[23]= |
|
This work is licensed under a Creative Commons Attribution 4.0 International License