Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 FindCanonicalWolframModel

Source Notebook

Attempt to find a canonical representation for a Wolfram model

Contributed by: Ed Pegg

ResourceFunction["FindCanonicalWolframModel"][rule]

attempts to find a canonical version of the specified Wolfram model rule.

ResourceFunction["FindCanonicalWolframModel"][list]

attempts to find a canonical version of the specified list of tuples.

Details and Options

The canonicalization follows several rules:
Tuples are sorted by length with longest tuples occurring first
Tuples of the same length on the same side of a rule are considered a rule part
A rule part with three tuples of length 2 has signature 32
Rule part are ordered so that new alphabet terms are introduced with maximal frugality
ResourceFunction["FindCanonicalWolframModel"] uses a heuristic method and may not give a complete canonical form in all cases.
ResourceFunction["FindCanonicalWolframModel"] has option PerformanceGoal. Possible settings include:
"Quality"try to get a true canonicalization
"Speed"get whatever canonicalization can be obtained quickly

Examples

Basic Examples (2) 

Attempt to find a canonical representation for a given Wolfram model:

In[1]:=
ResourceFunction[ "FindCanonicalWolframModel"][{{2, 3, 3}} -> {{3, 2, 2}, {2, 1, 1}}]
Out[1]=

Rename nodes and re-sort rules to find a canonical form:

In[2]:=
ResourceFunction[ "FindCanonicalWolframModel"][{{{2, 3, 3}} -> {{3, 2, 2}, {2, 1, 1}}, {{a, e, d}, {d, c}, {c, b}, {b, a}} -> {{}}}]
Out[2]=

A slightly more complicated case:

In[3]:=
ResourceFunction[ "FindCanonicalWolframModel"][{{0, 1}, {0, 2}, {0, 3}} -> {{4, 5}, {5, 4}, {4, 6}, {6, 4}, {5, 6}, {6, 5}, {4, 1}, {5, 2}, {6, 3}, {1, 6}, {3, 4}}]
Out[3]=

Scope (2) 

FindCanonicalWolframModel can handle any names for elements:

In[4]:=
ResourceFunction[ "FindCanonicalWolframModel"][{{a, e, d}, {d, c}, {c, b}, {b, a}} -> {{}}]
Out[4]=
In[5]:=
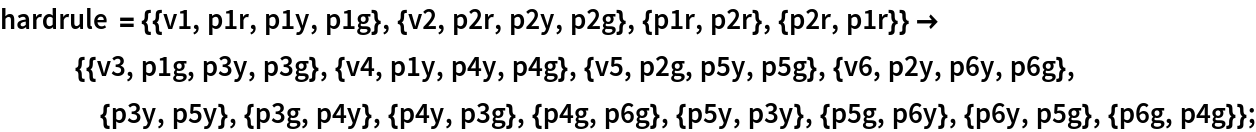hardrule = {{v1, p1r, p1y, p1g}, {v2, p2r, p2y, p2g}, {p1r, p2r}, {p2r, p1r}} -> {{v3, p1g, p3y, p3g}, {v4, p1y, p4y, p4g}, {v5, p2g, p5y, p5g}, {v6, p2y, p6y, p6g}, {p3y, p5y}, {p3g, p4y}, {p4y, p3g}, {p4g, p6g}, {p5y, p3y}, {p5g, p6y}, {p6y, p5g}, {p6g, p4g}};
In[6]:=
ResourceFunction["FindCanonicalWolframModel"][hardrule]
Out[6]=
In[7]:=
difficult = {{8, 5, 9, 5}, {4, 11, 6, 12}, {10, 6, 0, 13}, {7, 11, 1, 8}, {0, 5, 7, 7}, {13, 9, 6, 5}, {3, 1, 6, 8}, {8, 2, 5, 13}, {9, 5, 4, 4}, {9, 2, 13, 0}, {6, 10, 6, 2}, {11, 6, 1, 10}, {3, 9, 4, 4}, {7, 6, 2, 8}, {7, 8, 8, 2}} -> {{5, 9, 9, 11}, {0, 1, 6, 10}, {5, 5, 0, 0}, {3, 6, 12, 10}, {2, 9, 1, 2}, {12, 10, 1, 13}, {0, 1, 9, 0}, {2, 2, 0, 7}, {1, 11, 0, 5}, {2, 10, 5, 11}, {9, 2, 1, 0}, {4, 1, 10, 1}, {12, 10, 5, 10}, {4, 11, 2, 9}, {11, 10, 6, 7}};
In[8]:=
ResourceFunction["FindCanonicalWolframModel"][difficult]
Out[8]=

Some random lists of tuples that should have the same canonicalization:

In[9]:=
ScrambleList[list_] := Module[{alphabet = Union[Flatten[list]]}, RandomSample[list] /. Thread[alphabet -> RandomSample[alphabet]]];
In[10]:=
randomrulepart = RandomInteger[{1, 9}, {9, 3}]; scramble = Table[ScrambleList[randomrulepart], {5}]
Out[11]=

The canonical forms are all identical:

In[12]:=
ResourceFunction["FindCanonicalWolframModel"] /@ scramble
Out[12]=

Version History

  • 4.0.0 – 17 February 2020
  • 3.0.0 – 19 December 2019
  • 2.0.0 – 13 December 2019
  • 1.0.0 – 04 December 2019

Related Resources

License Information