Function Repository Resource:

FiedlerMatrix

Construct a Fiedler matrix from a vector

Contributed by: Arnoud Buzing

ResourceFunction["FiedlerMatrix"][vec]

gives the Fiedler matrix corresponding to the vector vec.

Details

Given a generating vector x, the resulting Fiedler matrix F has entries given by F〚i,j〛=Abs[x〚i〛-x〚j〛].

The Fiedler matrix is symmetric and has real eigenvalues, with one positive eigenvalue and all other eigenvalues being negative.

This matrix is not closely related to the matrix created by the resource function GeneralizedFiedlerMatrix.

Construct a Fiedler matrix:

In[1]:=

Out[1]=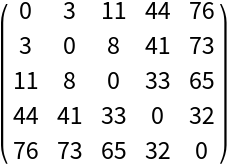

A function for the determinant of a Fiedler matrix:

In[2]:=

$fiedlerDet[v_?VectorQ] := Module[{n = Length[v]}, (-1)^(n - 1) 2^(n - 2) Apply[Times, Abs[ListCorrelate[{-1, 1}, v, 1]]]]$

Use it to compute the determinant:

In[3]:=

Out[3]=

Compare with the determinant computed using Det:

In[4]:=

Out[4]=

The inverse of a Fiedler matrix is cyclic tridiagonal (tridiagonal with extra elements in the upper right and lower left):

In[5]:=

Out[5]=