Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 FibonacciQ

Source Notebook

Check if a given number is a Fibonacci number

Contributed by: Navvye Anand

ResourceFunction["FibonacciQ"][n]

Checks if an integer n is a Fibonacci number.

Details

The Fibonacci sequence is a sequence of numbers denoted by the recurrence relation with and
Binet’s Formula provides a proof that a positive integer x is a Fibonacci number if and only if one of 5x2±4 is a perfect square.

Examples

Basic Examples (4) 

Check if F100 is a Fibonacci number:

In[1]:=
ResourceFunction["FibonacciQ"][354224848179261915075]
Out[1]=

Check if an integer of the magnitude is a Fibonacci Number:

In[2]:=
ResourceFunction["FibonacciQ"][10^7 + 9649]
Out[2]=

FibonacciQ works on negative numbers as well:

In[3]:=
ResourceFunction["FibonacciQ"][-8]
Out[3]=

Verify Fibonacci[n]:

In[4]:=
AllTrue[Table[ ResourceFunction["FibonacciQ"][Fibonacci[i]], {i, 1, 100}], TrueQ]
Out[4]=

Possible Issues (1) 

FibonacciQ only works for integers:

In[5]:=
ResourceFunction["FibonacciQ"][8.0000000000001]
Out[5]=

Neat Examples (2) 

Check the frequency of Fibonacci Numbers:

In[6]:=
ListLinePlot[ Table[Last[ First[Tally[ResourceFunction["FibonacciQ"][#] & /@ Range[n]]]]/ n, {n, 10, 10000, 10}], PlotRange -> All, PlotLabel -> "Decreasing Frequency of Fibonacci Numbers"]
Out[6]=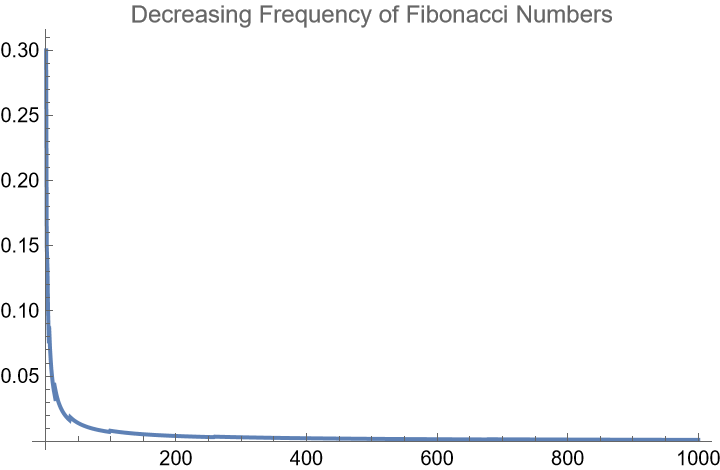

Check the first differences of number of states of a Multiway System are Fibonacci Numbers:

In[7]:=
FibonacciGrammar = {"x" -> "xA", "x" -> "yB", "y" -> "xA"}; init = "x";
In[8]:=
Table[ResourceFunction["MultiwaySystem"][FibonacciGrammar, init, n, "StatesGraph"], {n, 1, 4, 1}]
Out[8]=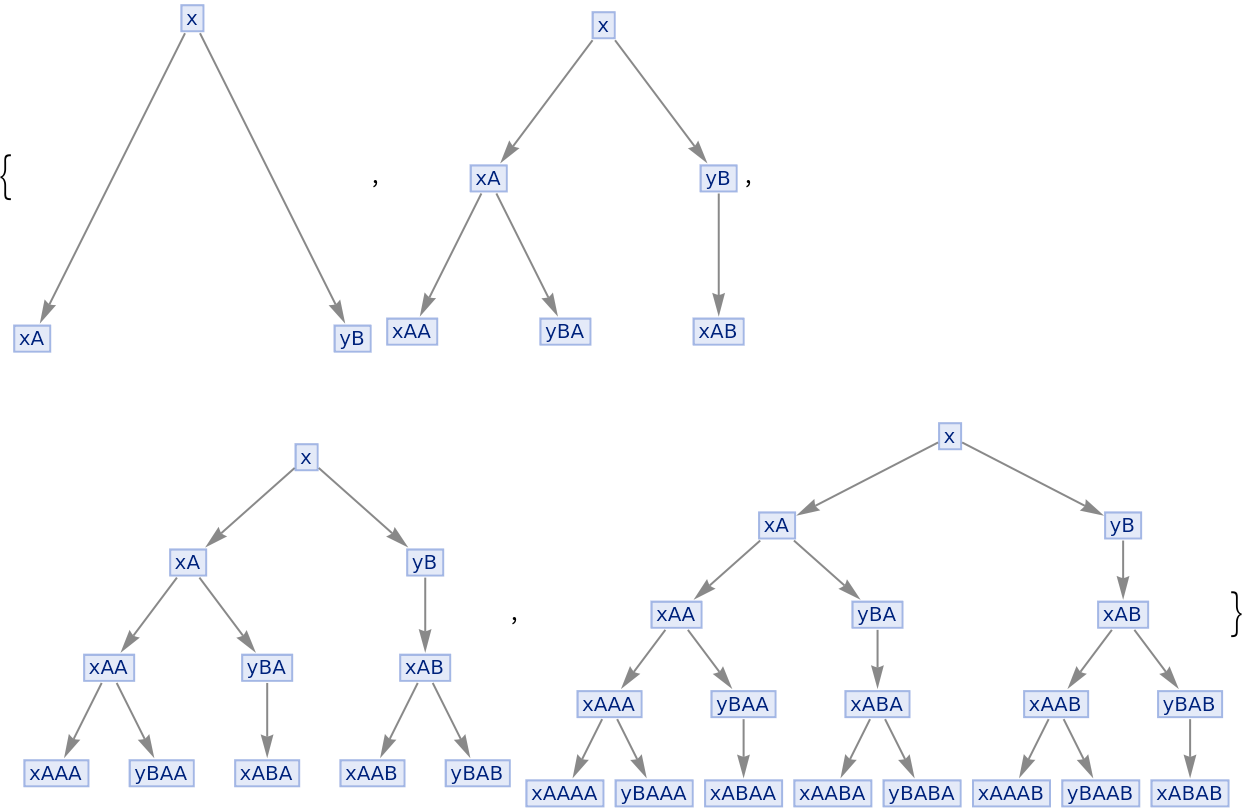
In[9]:=
data = Differences[ Table[VertexCount[ ResourceFunction["MultiwaySystem"][{"x" -> "xA", "x" -> "yB", "y" -> "xA"}, "x", n, "StatesGraph"]], {n, 1, 20, 1}]]
Out[9]=
In[10]:=
ResourceFunction["FibonacciQ"] /@ data
Out[10]=

Publisher

Navvye Anand

Requirements

Wolfram Language 13.0 (December 2021) or above

Version History

  • 1.0.0 – 06 May 2024

Source Metadata

  • Citation:
    • "Wikipedia Contributors. 'Fibonacci Sequence.' Wikipedia, The Free Encyclopedia, Wikipedia Foundation, 5 May 2024, en.wikipedia.org/wiki/Fibonacci_sequence#Recognizing_Fibonacci_numbers."

Related Resources

Author Notes

No limitations!

License Information