Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 FareySunburst

Source Notebook

Create a Farey sunburst

Contributed by: Sander Huisman

ResourceFunction["FareySunburst"][n]

creates a Farey sunburst of order n.

Details

A Farey sunburst is constructed by using the numerators and denominators of the Farey sequence and interpreting those pairs as coordinates. The point are then mirrored to create a closed polygon that looks like a star.
The order n should be a positive integer.

Examples

Basic Examples (2) 

Create a Farey sunburst of order 3:

In[1]:=
ResourceFunction["FareySunburst"][3]
Out[1]=

Visualize it:

In[2]:=
Graphics[ResourceFunction["FareySunburst"][3]]
Out[2]=

Visualize the first 5, scaled to a standard height (see the Neat Example for an overlap example):

In[3]:=
Graphics[ResourceFunction["FareySunburst"][#]] & /@ Range[5] // Row
Out[3]=

Properties and Relations (2) 

Compute the areas of the first few Farey sunbursts:

In[4]:=
Table[Area[ResourceFunction["FareySunburst"][k]], {k, 9}]
Out[4]=

Compare with an explicit formula:

In[5]:=
Table[4 Sum[EulerPhi[j], {j, k}], {k, 9}]
Out[5]=

Neat Examples (3) 

Create a complicated pattern:

In[6]:=
Graphics[ Translate[ResourceFunction["FareySunburst"][20], Catenate@Table[20 {i, j}, {i, -2, 2}, {j, -2, 2}]]]
Out[6]=

Overlap the first ten Farey sunbursts:

In[7]:=
colors = ColorData["Rainbow"] /@ Subdivide[10 - 1]; Graphics[ Reverse@Table[{colors[[n]], ResourceFunction["FareySunburst"][n]}, {n, 10}]]
Out[8]=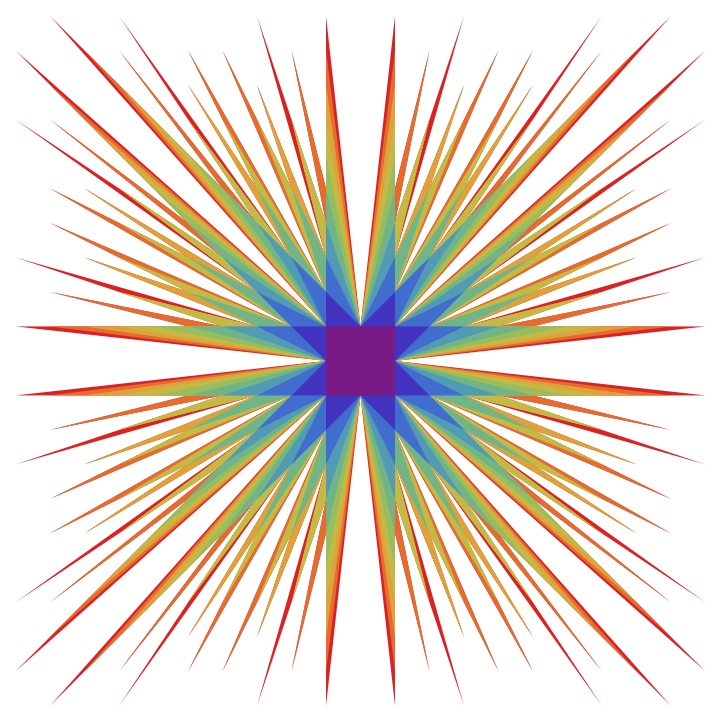

Arrange Farey sunbursts in a Sierpiński carpet:

In[9]:=
With[{r = 3, n = 4}, MeshPrimitives[MengerMesh[r], 2] /. p_Polygon :> With[{pts = First[p]}, Polygon[RescalingTransform[{{-n, n}, {-n, n}}, MinMax /@ Transpose[pts]][ First@ResourceFunction["FareySunburst"][n]]]]] // Graphics
Out[9]=

Publisher

SHuisman

Requirements

Wolfram Language 12.3 (May 2021) or above

Version History

  • 1.0.0 – 20 December 2023

Related Resources

License Information