Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 FaddeevaW

Source Notebook

Evaluate the Faddeeva function

Contributed by: Jan Mangaldan

ResourceFunction["FaddeevaW"][z]

gives the Faddeeva function w(z).

Details

Mathematical function, suitable for both symbolic and numerical manipulation.
ResourceFunction["FaddeevaW"][z] is given by w(z)=exp(-z2)erfc(-i​z).
For certain special arguments, ResourceFunction["FaddeevaW"] automatically evaluates to exact values.
ResourceFunction["FaddeevaW"] can be evaluated to arbitrary numerical precision.
ResourceFunction["FaddeevaW"] automatically threads over lists.

Examples

Basic Examples (4) 

Evaluate the Faddeeva function numerically:

In[1]:=
ResourceFunction["FaddeevaW"][0.95]
Out[1]=

Plot the real and imaginary parts over a subset of the reals:

In[2]:=
ReImPlot[ResourceFunction["FaddeevaW"][z], {z, -5, 5}, PlotLegends -> "ReIm"]
Out[2]=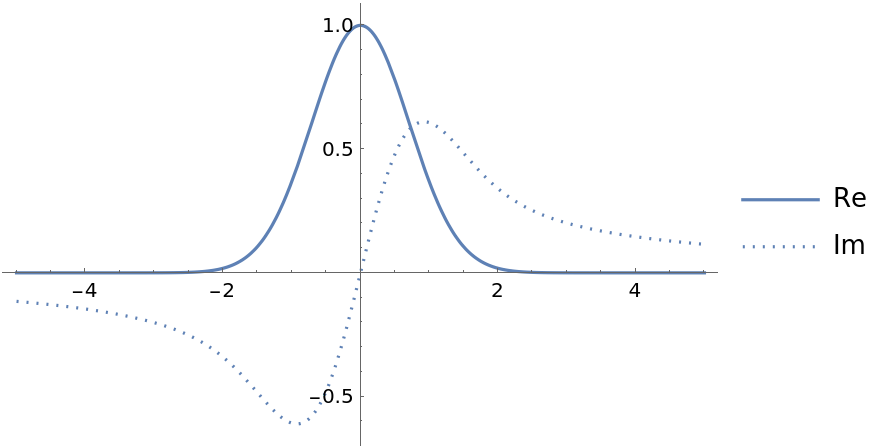

Plot over a subset of the complexes:

In[3]:=
ComplexPlot3D[ ResourceFunction["FaddeevaW"][z], {z, -2 - 2 I, 2 + 2 I}, PlotLegends -> Automatic]
Out[3]=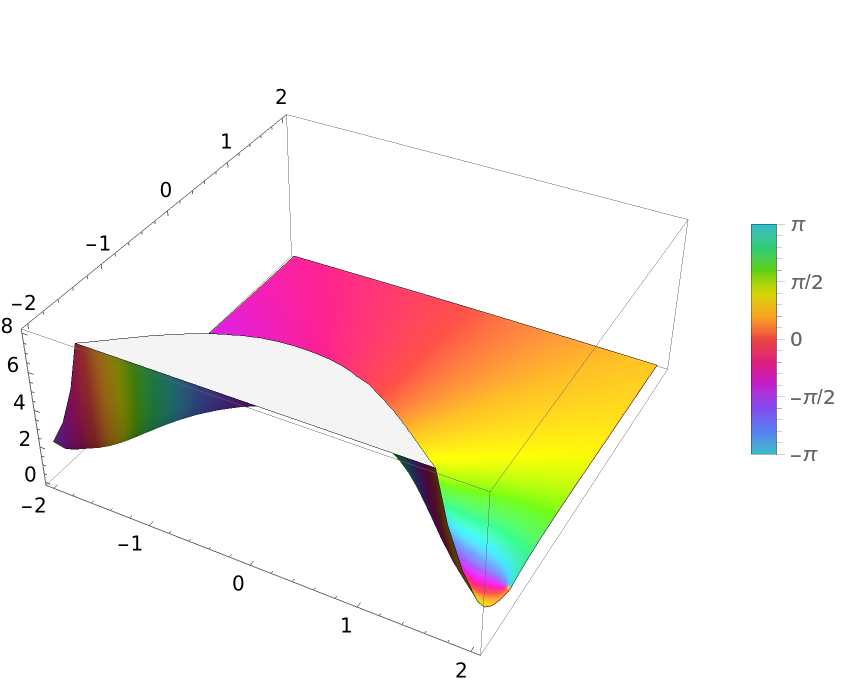

Series expansion at the origin:

In[4]:=
Series[ResourceFunction["FaddeevaW"][z], {z, 0, 10}]
Out[4]=

Scope (4) 

Evaluate for complex arguments:

In[5]:=
ResourceFunction["FaddeevaW"][1.5 - I]
Out[5]=

Evaluate to high precision:

In[6]:=
N[ResourceFunction["FaddeevaW"][3/2], 30]
Out[6]=

The precision of the output tracks the precision of the input:

In[7]:=
ResourceFunction["FaddeevaW"][1.5000000000000000000000000000]
Out[7]=

FaddeevaW threads elementwise over lists:

In[8]:=
ResourceFunction["FaddeevaW"][{0.5, 1.0, 1.5}]
Out[8]=

Simple exact values are generated automatically:

In[9]:=
ResourceFunction["FaddeevaW"][0]
Out[9]=

Applications (1) 

Visualize the altitude chart for w(z):

In[10]:=
Show[ContourPlot[ Abs[ResourceFunction["FaddeevaW"][x + I y]], {x, 0, 3 + 1/5}, {y, -3, 3}, Sequence[Contours -> Join[ Subdivide[10], {2, 3, 4, 5, 10, 100}], ContourShading -> None, ContourStyle -> ColorData[97, 1], PlotPoints -> 55]], ContourPlot[ Arg[ResourceFunction["FaddeevaW"][x + I y]], {x, 0, 3 + 1/5}, {y, -3, 3}, Sequence[Contours -> Pi Union[ Subdivide[-1, 1, 6], Range[9]/18], ContourShading -> None, ContourStyle -> ColorData[97, 2], PlotPoints -> 55]], AspectRatio -> Automatic]
Out[10]=

Properties and Relations (6) 

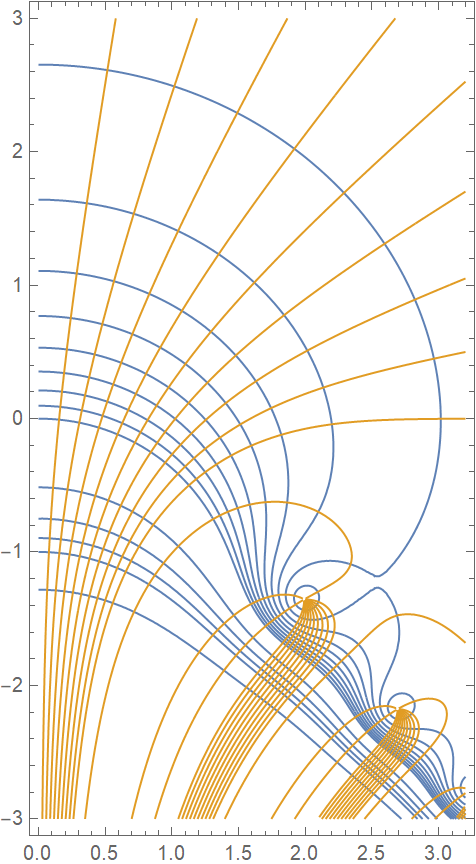Compare FaddeevaW with its integral representation:

In[11]:=
With[{x = 2}, N[{ResourceFunction["FaddeevaW"][x], E^-x^2 (1 + (2 I)/Sqrt[\[Pi]] \!\( \*SubsuperscriptBox[\(\[Integral]\), \(0\), \(x\)]\( \*SuperscriptBox[\(E\), SuperscriptBox[\(u\), \(2\)]] \[DifferentialD]u\)\))}]]
Out[11]=

Verify reflection properties of FaddeevaW:

In[12]:=
With[{z = 2 + 3 I}, N[{ResourceFunction["FaddeevaW"][-z], 2 E^-z^2 - ResourceFunction["FaddeevaW"][z]}]]
Out[12]=
In[13]:=
With[{z = 2 + 3 I}, N[{ResourceFunction["FaddeevaW"][Conjugate[z]], Conjugate[ResourceFunction["FaddeevaW"][-z]]}]]
Out[13]=

Derivatives of FaddeevaW can be expressed in terms of FaddeevaW:

In[14]:=
D[ResourceFunction["FaddeevaW"][z], {z, 5}] // Simplify
Out[14]=

DawsonF can be expressed in terms of FaddeevaW:

In[15]:=
With[{x = 5}, N[{DawsonF[x], (I Sqrt[\[Pi]])/ 2 (E^-x^2 - ResourceFunction["FaddeevaW"][x])}] // Chop]
Out[15]=

FresnelF and FresnelG can be expressed in terms of FaddeevaW:

In[16]:=
With[{x = 5}, N[{FresnelG[x] + I FresnelF[x], (1 + I)/ 2 ResourceFunction["FaddeevaW"][Sqrt[\[Pi]]/2 (1 + I) x]}]]
Out[16]=

The PDF of VoigtDistribution can be expressed in terms of FaddeevaW:

In[17]:=
With[{\[Delta] = 3/4, \[Sigma] = 8/5, x = 2}, N[{PDF[VoigtDistribution[\[Delta], \[Sigma]], x], Re[1/(\[Sigma] Sqrt[2 \[Pi]]) ResourceFunction["FaddeevaW"][(x + I \[Delta])/( Sqrt[2] \[Sigma])]]}] // Chop]
Out[17]=

Possible Issues (1) 

Very large arguments can fail to produce results:

In[18]:=
ResourceFunction["FaddeevaW"][-10.^100 I]
Out[18]=

Neat Examples (1) 

Plot a Cornu spiral:

In[19]:=
ParametricPlot[ ReIm[Exp[I t^2] ResourceFunction["FaddeevaW"][ t Exp[I \[Pi]/4]]], {t, -7, 7}, Axes -> None, Frame -> True]
Out[19]=

Version History

  • 1.0.0 – 15 January 2021

Source Metadata

  • Citation:
    • Abrarov S.M., Quine B.M., "A rational approximation of the Dawson's integral for efficient computation of the complex error function." Applied Mathematics and Computation, vol. 321, 526-543, 2018. DOI: 10.1016/j.amc.2017.10.032

Related Resources

License Information