Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 FactorialSeriesExpansion

Source Notebook

Expand a function into a factorial series

Contributed by: Jan Mangaldan

ResourceFunction["FactorialSeriesExpansion"][expr,z,n]

gives the nth-order factorial series expansion of expr in z.

Details

A factorial series is also known as an inverse factorial series.
The factorial series expansion of a function is expressed in the form , where is Pochhammer[z,k].
The factorial series expansion can be constructed for any function that can be expanded about the point z=∞.

Examples

Basic Examples (1) 

Find the 3rd-order factorial series of e1/x:

In[1]:=
ResourceFunction["FactorialSeriesExpansion"][E^(1/x), x, 3]
Out[1]=
In[2]:=
Plot[%, {x, 1, 5}]
Out[2]=

Scope (3) 

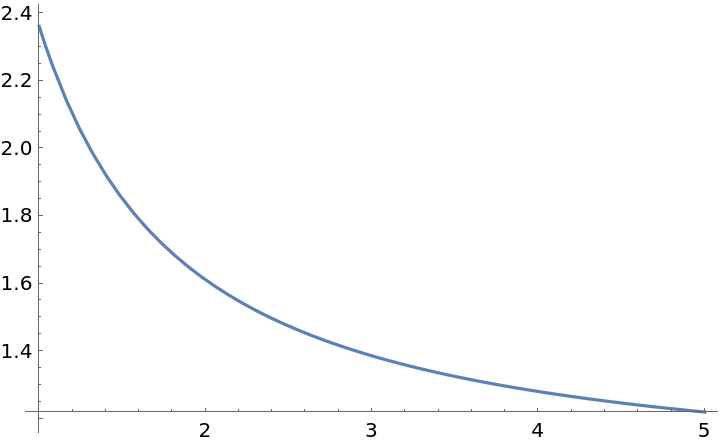Find the 5th-order factorial series of the arctangent:

In[3]:=
ResourceFunction["FactorialSeriesExpansion"][ArcTan[z], z, 5]
Out[3]=

Find the 3rd-order factorial series of :

In[4]:=
ResourceFunction["FactorialSeriesExpansion"][LogGamma[z], z, 3]
Out[4]=

Factorial series for a special case of MeijerG:

In[5]:=
ResourceFunction["FactorialSeriesExpansion"][ MeijerG[{{0}, {}}, {{0, 0, 0}, {}}, z], z, 7]
Out[5]=

Applications (1) 

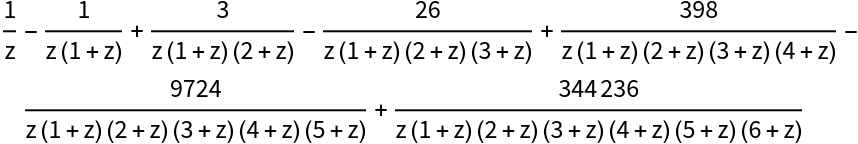The factorial series expansion of a function usually has better numerical properties than the corresponding asymptotic series:

In[6]:=
asympSer[z_] = Normal[Series[Exp[z] ExpIntegralE[1, z], {z, \[Infinity], 12}]]; facSer[z_] = ResourceFunction["FactorialSeriesExpansion"][ Exp[z] ExpIntegralE[1, z], z, 12];
In[7]:=
{asympSer[z], facSer[z], Exp[z] ExpIntegralE[1, z]} /. z -> 5.2
Out[7]=
In[8]:=
Plot[{Exp[z] ExpIntegralE[1, z], asympSer[z], facSer[z]}, {z, 1, 12}, PlotLegends -> {"original", "asymptotic series", "factorial series"}, PlotStyle -> {Thick, Dashed, Dashed}]
Out[8]=

Properties and Relations (1) 

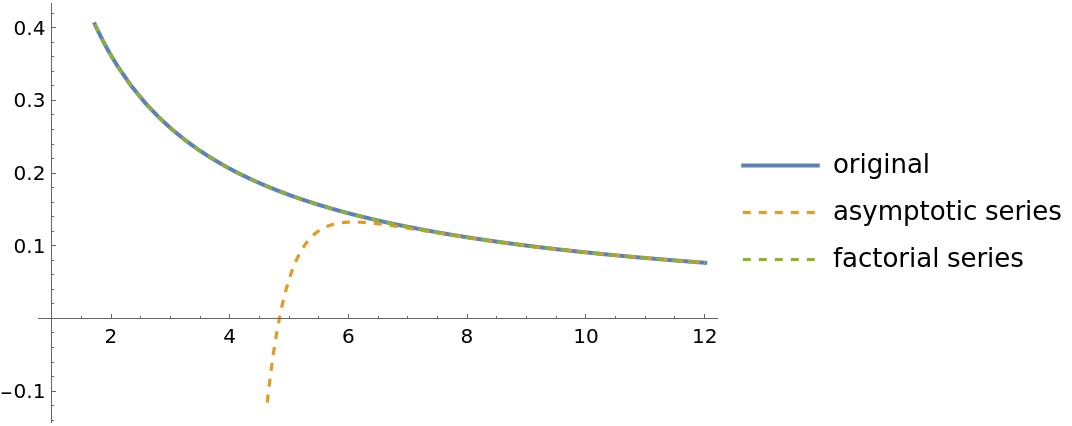The factorial series of is the function itself:

In[9]:=
ResourceFunction["FactorialSeriesExpansion"][1/Pochhammer[z, 4], z, 5]
Out[9]=

Version History

  • 1.0.0 – 22 March 2021

Source Metadata

  • Citation:
    • Watson G.N., "The transformation of an asymptotic series into a convergent series of inverse factorials." Rendiconti del Circolo Matematico di Palermo, vol. 34, 41-88, 1912. DOI: 10.1007/BF03015008
    • Weniger E.J., "Summation of divergent power series by means of factorial series." Applied Numerical Mathematics, vol. 60, no. 12, 1429-1441, 2010. DOI: 10.1016/j.apnum.2010.04.003

Related Resources

License Information