Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Evaluate the Fabius function
ResourceFunction["FabiusF"][x] computes the Fabius function. |
Plot the Fabius function:
| In[1]:= |
| Out[1]= |  |
Evaluate at an integer:
| In[2]:= |
| Out[2]= |
Evaluate at a dyadic rational (a rational number whose denominator is a power of two):
| In[3]:= |
| Out[3]= |
FabiusF does not automatically evaluate for arguments that are not a dyadic rational number:
| In[4]:= |
| Out[4]= |
Evaluate numerically:
| In[5]:= |
| Out[5]= |
Evaluate to arbitrary precision:
| In[6]:= |
| Out[6]= |
The precision of the output tracks the precision of the input:
| In[7]:= |
| Out[7]= |
FabiusF threads over lists:
| In[8]:= |
| Out[8]= |
The Fabius function for odd integer arguments can be expressed in terms of ThueMorse:
| In[9]:= |
| Out[9]= |
Functional differential equation for the Fabius function:
| In[10]:= |
| Out[10]= |
Higher derivatives of the Fabius function can be expressed in terms of the function itself:
| In[11]:= |
| Out[11]= |
FabiusF is undefined for complex numbers:
| In[12]:= |
| Out[12]= |
Plot a parametric function defined in terms of FabiusF:
| In[13]:= |
| Out[13]= | 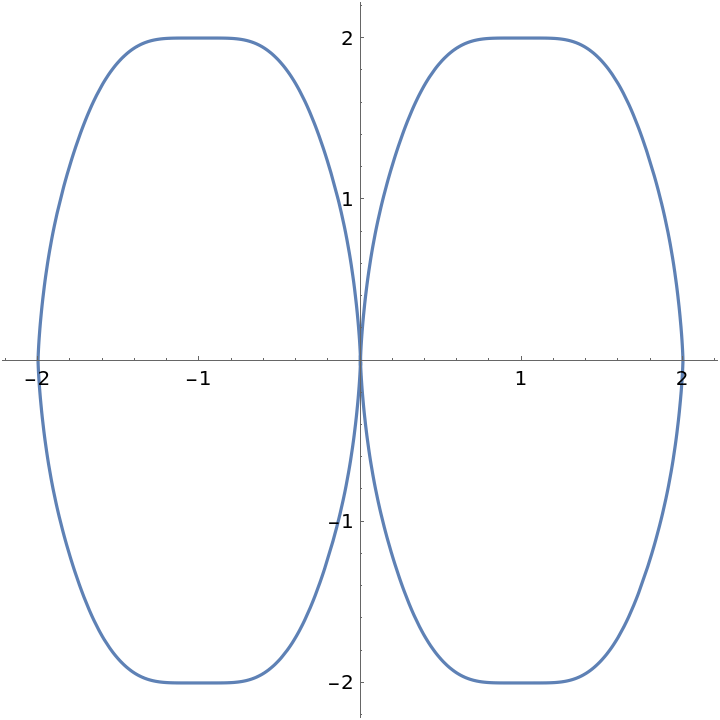 |
This work is licensed under a Creative Commons Attribution 4.0 International License