Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Produce random spatial graphs by sprinkling points into a Riemannian manifold with an arbitrary extrinsic curvature
ResourceFunction["ExtrinsicCurvedManifoldToGraph"][cond,{x1,…,xm},n] produces a random sprinkling of n points into a Riemannian manifold with extrinsic curvature satisfying the conditions cond, assuming a discreteness scale of 1. | |
ResourceFunction["ExtrinsicCurvedManifoldToGraph"][cond,{x1,…,xm},disc,n] produces a random sprinkling of n points with discreteness scale disc into a Riemannian manifold with extrinsic curvature satisfying the conditions cond. | |
ResourceFunction["ExtrinsicCurvedManifoldToGraph"][cond,{x1,…,xm},{{xmin,xmax},…},n] produces a random sprinkling of n points into a Riemannian manifold with extrinsic curvature satisfying the conditions cond restricted to the bounds {xmin,xmax}×…, assuming a discreteness scale of 1. | |
ResourceFunction["ExtrinsicCurvedManifoldToGraph"][cond,{x1,…,xm},{{xmin,xmax},…},disc,n] uses discreteness scale disc. | |
ResourceFunction["ExtrinsicCurvedManifoldToGraph"][…,"prop"] gives the property "prop" for the Riemannian manifold sprinkling with the specified extrinsic curvature. |
| "SpatialGraph" | spatial graph with vertex coordinates given by the underlying manifold coordinates |
| "Points" | plot of the sprinkled points only (without spatial edges) |
| "PointsList" | list of the manifold coordinates of all sprinkled points |
| "DiscretenessScale" | discreteness scale of the sprinkling |
| "PointsCount" | number of sprinkled points |
| "Dimensions" | number of dimensions in the continuum manifold approximation |
| "EdgeCount" | total number of spatial edges |
| "PureSpatialGraph" | spatial graph with vertex coordinate information removed |
| "Properties" | list of properties |
Produce a random sprinkling of 100 points into a 2-dimensional Riemannian manifold with a hyperbolic extrinsic curvature condition, with discreteness scale 0.8:
| In[1]:= |
|
| Out[1]= |

|
Show the spatial graph:
| In[2]:= |
|
| Out[2]= |
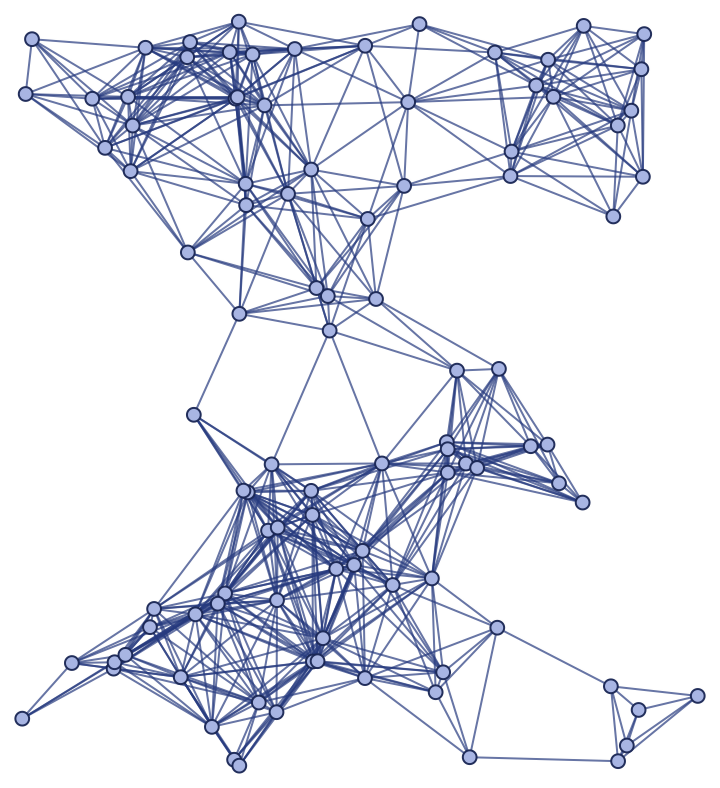
|
Show the pure spatial graph (with vertex coordinate information removed):
| In[3]:= |
|
| Out[3]= |
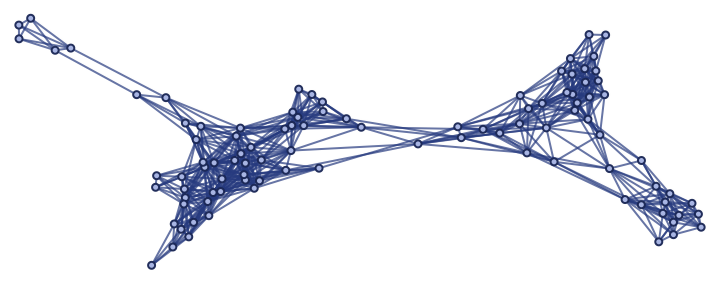
|
Produce a random sprinkling of 200 points into a 3-dimensional Riemannian manifold with a hyperboloidal extrinsic curvature condition, with discreteness scale 1.2:
| In[4]:= |
|
| Out[4]= |

|
Show the spatial graph:
| In[5]:= |
|
| Out[5]= |

|
Show the pure spatial graph (with vertex coordinate information removed):
| In[6]:= |
|
| Out[6]= |
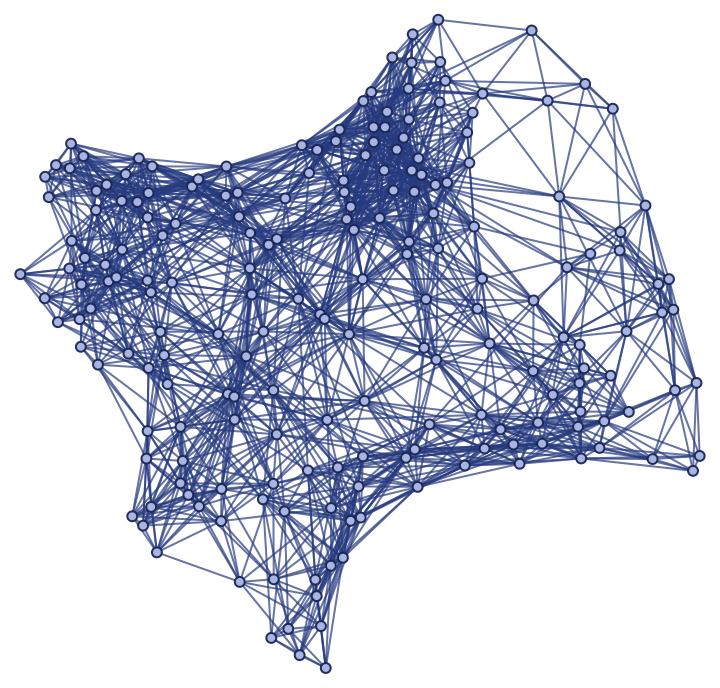
|
Plot the positions of the sprinkled points only (without spatial edges):
| In[7]:= |
|
| Out[7]= |

|
Produce a random sprinkling of 200 points into a 3-dimensional Riemannian manifold with a paraboloidal extrinsic curvature condition based on Flamm's paraboloid (related to the Schwarzschild geometry), with discreteness scale 0.3:
| In[8]:= |
|
| Out[8]= |

|
Plot the positions of the sprinkled points only (without spatial edges):
| In[9]:= |
|
| Out[9]= |

|
Show the spatial graph:
| In[10]:= |
|
| Out[10]= |
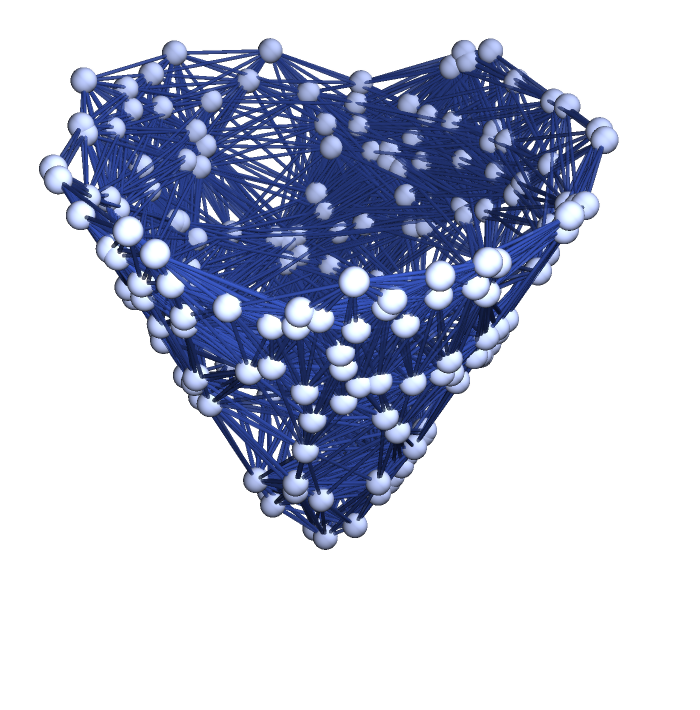
|
Show the pure spatial graph (with vertex coordinate information removed):
| In[11]:= |
|
| Out[11]= |

|
By default, the discreteness scale is assumed to be equal to 1:
| In[12]:= |
|
| Out[12]= |

|
Show the spatial graph:
| In[13]:= |
|
| Out[13]= |

|
By default, the manifold region is restricted to the bounds {{-1,1},…}:
| In[14]:= |
|
| Out[14]= |

|
Show the spatial graph:
| In[15]:= |
|
| Out[15]= |

|
Sprinklings can be produced in 1-dimensional Riemannian manifolds:
| In[16]:= |
|
| Out[16]= |

|
Show the spatial graph:
| In[17]:= |
|
| Out[17]= |
|
Produce a sprinkling in a 2-dimensional Riemannian manifold:
| In[18]:= |
|
| Out[18]= |

|
Show the spatial graph:
| In[19]:= |
|
| Out[19]= |
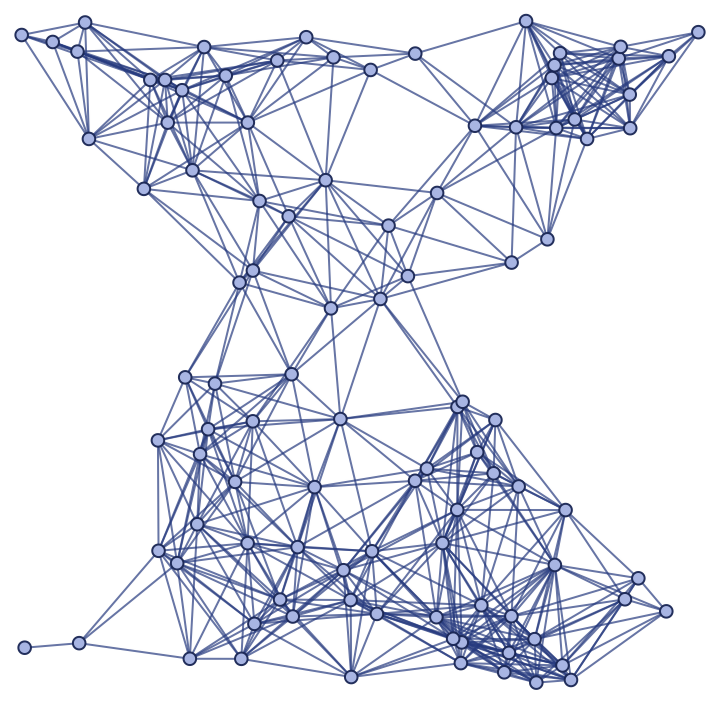
|
Produce a sprinkling in a 3-dimensional Riemannian manifold:
| In[20]:= |
|
| Out[20]= |

|
Show the spatial graph. Note that, unlike the resource function FlatManifoldToGraph, ExtrinsicCurvedManifoldToGraph does not support higher-dimensional sprinklings:
| In[21]:= |
|
| Out[21]= |

|
Properties can be requested directly from ExtrinsicCurvedManifoldToGraph:
| In[22]:= |
|
| Out[22]= |

|
Produce a random sprinkling of 200 points into a 2-dimensional Riemannian manifold with hyperboloidal extrinsic curvature condition, with discreteness scale 1.2:
| In[23]:= |
|
| Out[23]= |

|
Show the complete list of properties:
| In[24]:= |
|
| Out[24]= |
|
Show the spatial graph:
| In[25]:= |
|
| Out[25]= |

|
Plot the positions of the sprinkled points only (without spatial edges):
| In[26]:= |
|
| Out[26]= |

|
Show a complete list of manifold coordinates for the sprinkled points:
| In[27]:= |
|
| Out[27]= |

|
Show the discreteness scale:
| In[28]:= |
|
| Out[28]= |
|
Show the number of dimensions in the background manifold:
| In[29]:= |
|
| Out[29]= |
|
Show the total number of spatial edges:
| In[30]:= |
|
| Out[30]= |
|
Show the pure spatial graph (with vertex coordinate information removed):
| In[31]:= |
|
| Out[31]= |
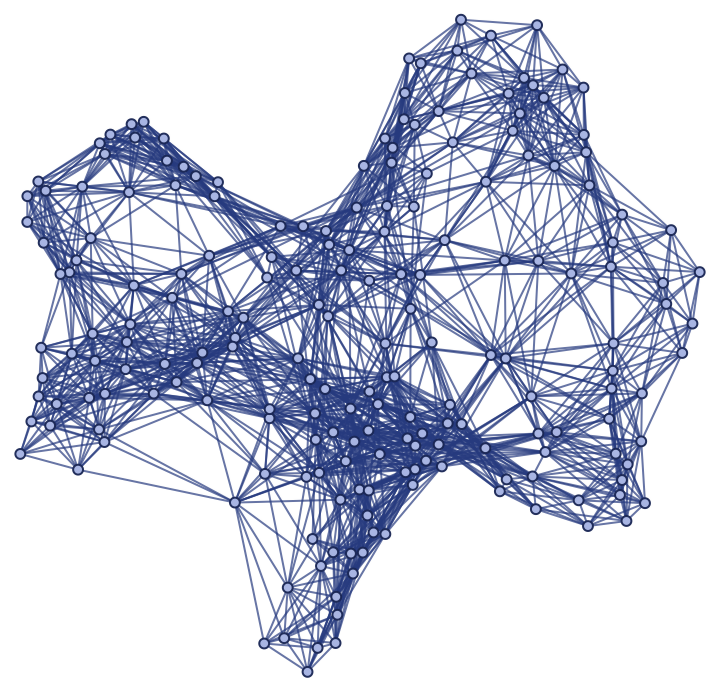
|
This work is licensed under a Creative Commons Attribution 4.0 International License