Basic Examples (5) 

Create a set of polynomials:

In[1]:=

First compute its Groebner basis:

In[2]:=

Out[2]=

Compute the extended Groebner basis:

In[3]:=

Out[3]=

Check that the bases agree up to a constant factor:

In[4]:=

Out[4]=

Check the conversion matrix identity:

In[5]:=

Out[5]=

Scope (3) 

Here is a larger example:

In[6]:=

Out[7]=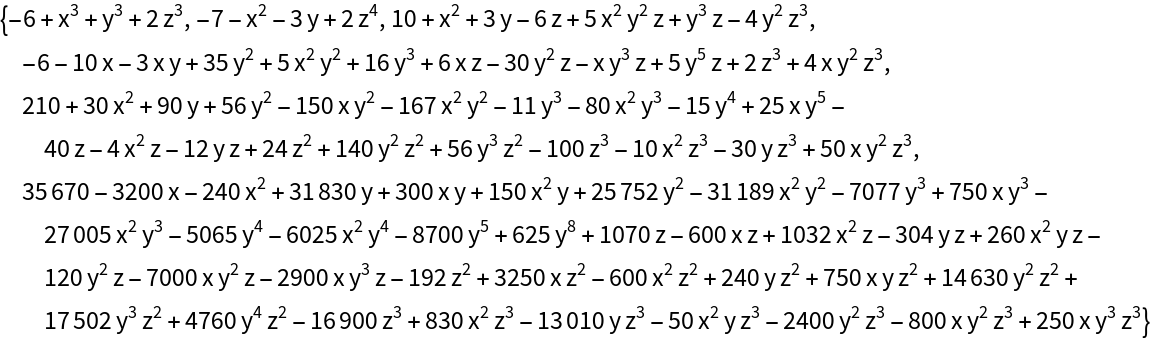

In[8]:=

Out[8]=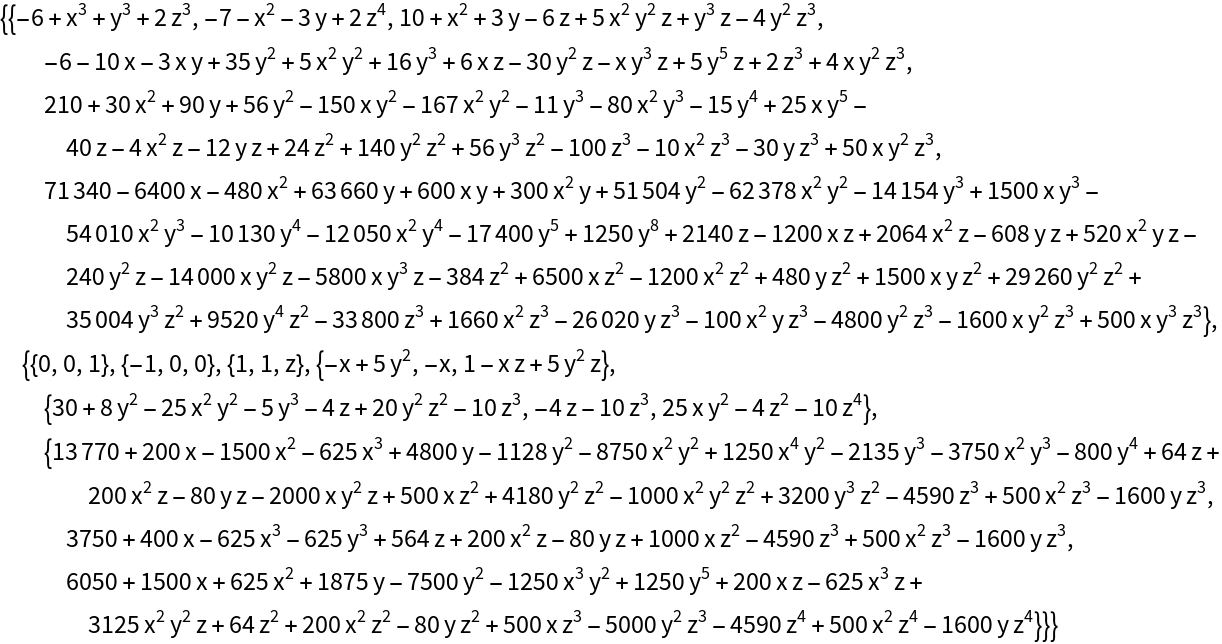

Check that the bases agree up to constant factors (they are not identical in this instance):

In[9]:=

Out[9]=

Check the conversion matrix identity:

In[10]:=

Out[10]=

Properties and Relations (7) 

The Groebner basis of a pair of univariate polynomials is their greatest common divisor, and similarly the extended Groebner basis gives the extended GCD. Create a pair of polynomials with a known common divisor poly1:

In[11]:=

Compute the extended GCD:

In[12]:=

Out[12]=

Check that the single polynomial in the Groebner basis is a GCD (a constant multiple of poly1):

In[13]:=

Out[13]=

Check the Bezout relation for the extended GCD:

In[14]:=

Out[14]=

Compare to PolynomialExtendedGCD:

In[15]:=

Out[15]=

Again check the Bezout relation:

In[16]:=

Out[16]=

Now check that these two computations agree up to a constant factor:

In[17]:=

Out[17]=

Possible Issues (1) 

ExtendedGroebnerBasis can be much slower that GroebnerBasis for the same input:

In[18]:=

Out[18]=

In[19]:=

Out[19]=