Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 ExtendedApart

Source Notebook

A partial fraction decomposition with the Extension option

Contributed by: Wolfram Staff (part of original concept by Dan McDonald)

ResourceFunction["ExtendedApart"][exp,var]

rewrites a rational expression as a sum of terms with minimal degree denominators in the complex domain, treating all variables other than var as constants.

ResourceFunction["ExtendedApart"][exp,var,Extension→{a1,a2,…}]

allows coefficients that are rational combinations of the algebraic numbers ai.

Details and Options

Similar to Apart, ResourceFunction["ExtendedApart"] gives the partial fraction decomposition of a rational expression.
ResourceFunction["ExtendedApart"] essentially adds the standard Extension option to Apart, with the default value Extension→All.
The possible values of the Extension option are the same as in Factor.
ResourceFunction["ExtendedApart"] automatically threads over lists.

Examples

Basic Examples (2) 

Decompose a rational expression into partial fractions:

In[1]:=
ResourceFunction["ExtendedApart"][1/(x^2 + 1), x]
Out[1]=

Compare with Apart:

In[2]:=
Apart[1/(x^2 + 1), x]
Out[2]=

Scope (5) 

Factor the denominator into linear factors:

In[3]:=
ResourceFunction["ExtendedApart"][1/(x^2 - 2), x]
Out[3]=

Decompose allowing complex coefficients:

In[4]:=
ResourceFunction["ExtendedApart"][1/(x^2 + a^2), x]
Out[4]=
In[5]:=
ResourceFunction["ExtendedApart"][1/(x^3 + 1), x]
Out[5]=
In[6]:=
ResourceFunction["ExtendedApart"][1/(x^4 + a^4), x]
Out[6]=
In[7]:=
Simplify /@ (ResourceFunction["ExtendedApart"][1/(1 + x + x^3), x] // ToRadicals) // TraditionalForm
Out[7]=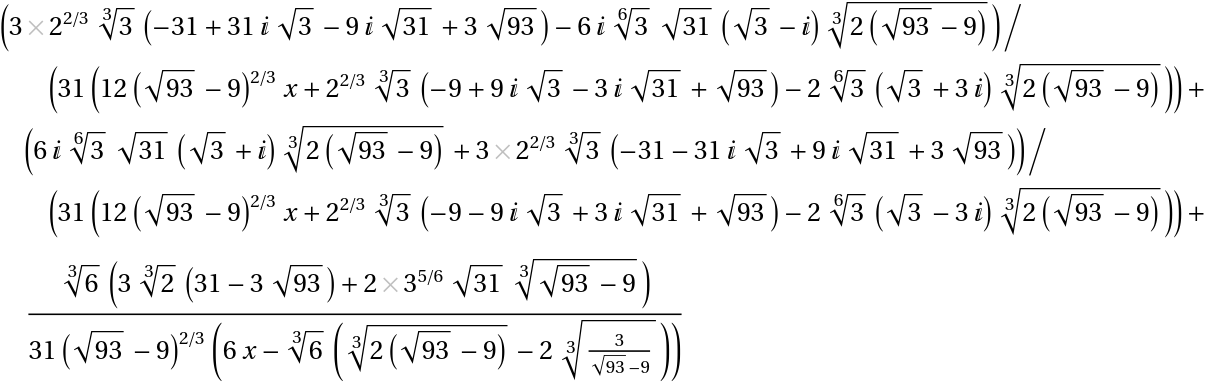

Allow the rationals extended by the algebraic number coefficients:

In[8]:=
ResourceFunction["ExtendedApart"][(1 + x)/(x^2 + 2 Sqrt[2] x + 2), x, Extension -> Automatic]
Out[8]=

Allow a finite algebraic extension of rationals:

In[9]:=
ResourceFunction["ExtendedApart"][1/(x^3 - 2), x, Extension -> 2^(1/3)]
Out[9]=

ExtendedApart threads over lists:

In[10]:=
ResourceFunction["ExtendedApart"][{1/(x^2 - 1), 1/(x^2 + 1)}, x]
Out[10]=

Properties and Relations (2) 

For some expressions, ExtendedApart gives results similar to Apart[Factor[exp]], with a proper Extension option for Factor:

In[11]:=
Factor[1/(x^2 + 1), Extension -> All] // Apart
Out[11]=
In[12]:=
ResourceFunction["ExtendedApart"][1/(x^2 + 1), x]
Out[12]=

Extension→I does not necessary uses the smallest denominators:

In[13]:=
ResourceFunction["ExtendedApart"][1/(x^4 + a^4), x, Extension -> I]
Out[13]=

Compare:

In[14]:=
ResourceFunction["ExtendedApart"][1/(x^4 + a^4), x, Extension -> All]
Out[14]=

Version History

  • 1.0.0 – 20 November 2020

Related Resources

License Information