Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Find the exspheres of a triangle or tetrahedron
ResourceFunction["Exspheres"][{p1,p2,p3}] constructs the excircles of the triangle defined by vertices p1,p2, and p3. | |
ResourceFunction["Exspheres"][{p1,p2,p3,p4}] constructs the exspheres of the tetrahedron defined by vertices p1,p2,p3 and p4. |
Find the excircles for a triangle:
| In[1]:= |
| Out[2]= |
Show the excircles, incircle and infinite lines:
| In[3]:= | ![Legended[
Graphics[{{ColorData[97, 1], InfiniteLine /@ Subsets[triangle, {2}]}, {ColorData[97, 4], circs}, {ColorData[97, 3], Insphere[triangle]}}], SwatchLegend[
ColorData[97] /@ {1, 3, 4}, {"triangle", "incircle", "excircles"}]]](https://www.wolframcloud.com/obj/resourcesystem/images/31f/31f8d6bc-f7d5-4254-965f-3f02fe648a84/0ba3438107370f5c.png) |
| Out[3]= | 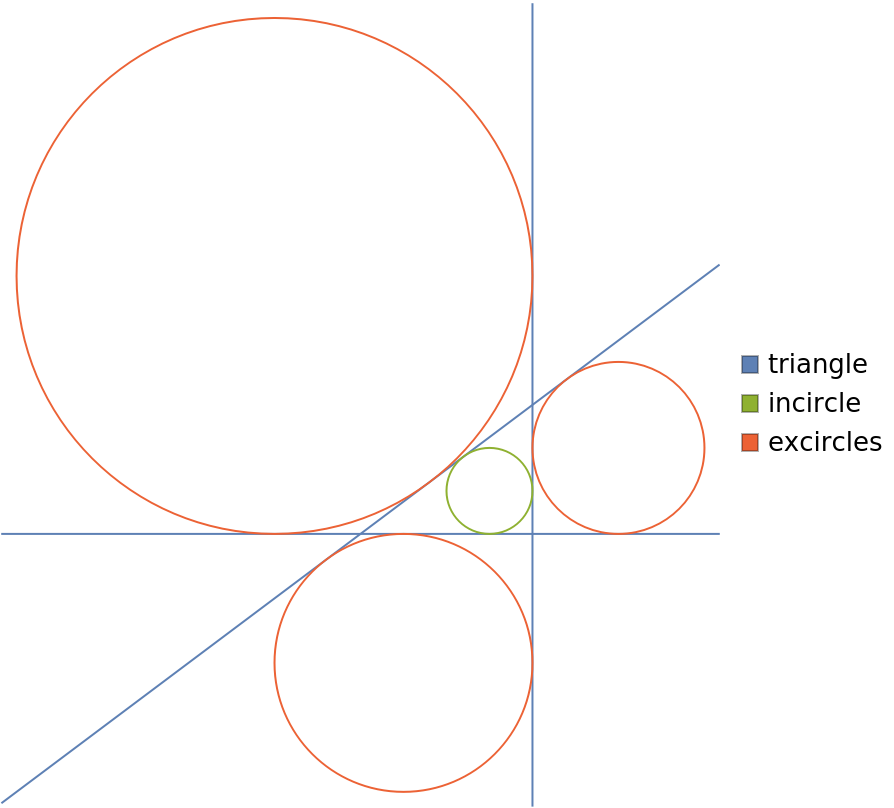 |
A triangle:
| In[4]:= |
| Out[4]= |  |
Show the triangle along with its excircles:
| In[5]:= | ![Graphics[{{FaceForm[ColorData[97, 1]], tri}, {Directive[AbsoluteThickness[5], ColorData[97, 1]], InfiniteLine /@ Partition[First[tri], 2, 1, 1]}, {Directive[
AbsoluteThickness[3], ColorData[97, 4]], ResourceFunction["Exspheres"][tri]}}]](https://www.wolframcloud.com/obj/resourcesystem/images/31f/31f8d6bc-f7d5-4254-965f-3f02fe648a84/5a1a521a515e3e7a.png) |
| Out[5]= |  |
Show a tetrahedron along with its exspheres:
| In[6]:= | ![BlockRandom[SeedRandom["tangencies", Method -> "ExtendedCA"];
tet = Tetrahedron[RandomPoint[Sphere[], 4]];
Graphics3D[{{Opacity[1/2], ColorData[97, 4], InfinitePlane /@ Subsets[PolyhedronCoordinates[tet], {3}]}, {FaceForm[], EdgeForm[AbsoluteThickness[4]], tet}, {Opacity[2/3], ColorData[97, 1], ResourceFunction["Exspheres"][tet]}}]]](https://www.wolframcloud.com/obj/resourcesystem/images/31f/31f8d6bc-f7d5-4254-965f-3f02fe648a84/6ec28d752557ce35.png) |
| Out[6]= | 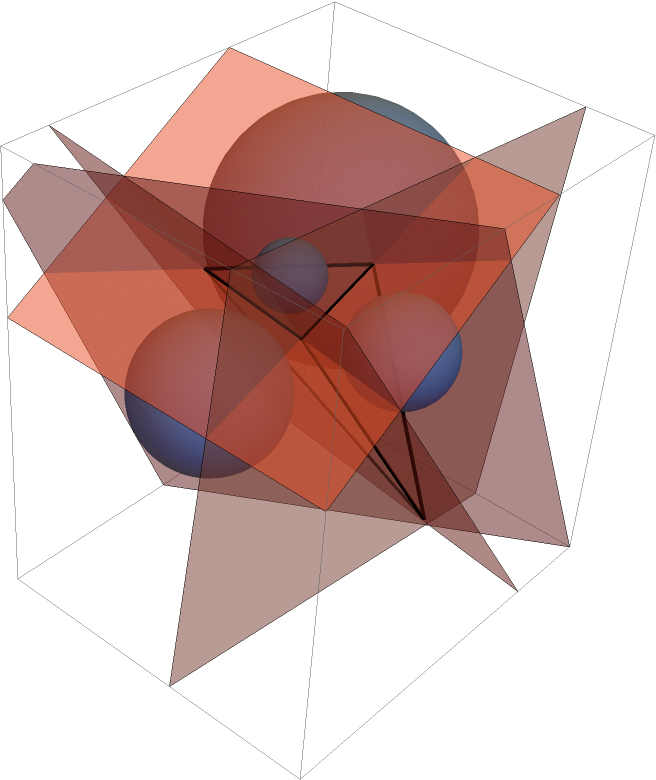 |
Show the insphere and exspheres of a regular tetrahedron:
| In[7]:= | ![With[{tet = Tetrahedron[]},
Graphics3D[{{ColorData[97, 1], Insphere[tet]}, {Opacity[2/3], ColorData[97, 3], ResourceFunction["Exspheres"][tet]}}, Boxed -> False]]](https://www.wolframcloud.com/obj/resourcesystem/images/31f/31f8d6bc-f7d5-4254-965f-3f02fe648a84/54eb8478552ae000.png) |
| Out[7]= | 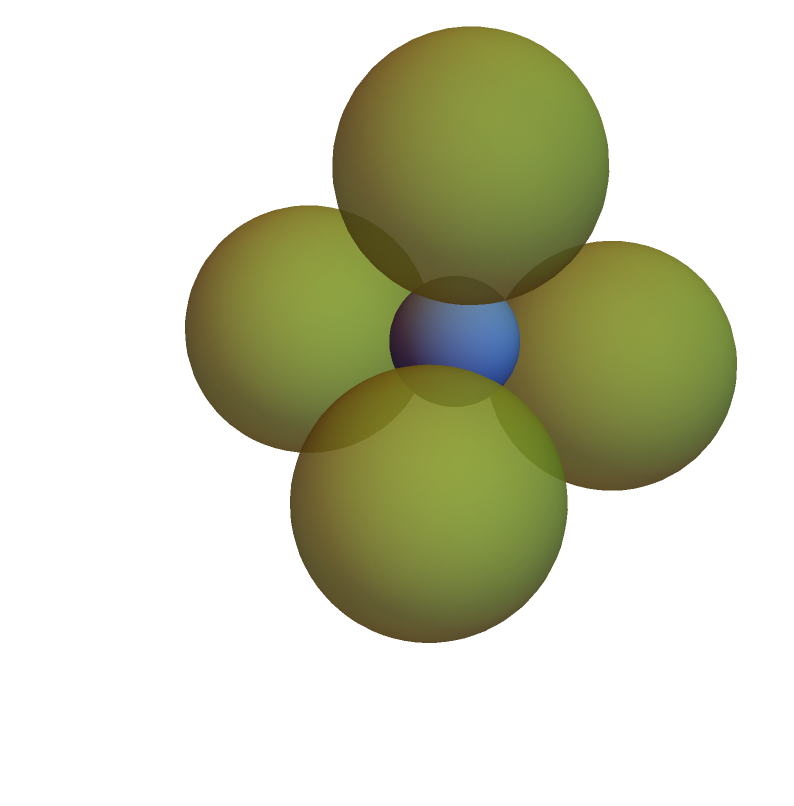 |
Show the excircles of an arbitrary triangle:
| In[8]:= | ![Manipulate[
Graphics[{EdgeForm[Blue], InfiniteLine /@ Subsets[{AA, BB, CC}, {2}],
Lighter[Brown], Triangle[{AA, BB, CC}], Green, ResourceFunction["Exspheres"][Triangle[{AA, BB, CC}]]}, PlotRange -> 6],
{{AA, {1, 3}}, {-4, -4}, {4, 4}, Locator}, {{BB, {-3, -1}}, {-4, -4}, {4, 4}, Locator}, {{CC, {2, -1}}, {-4, -4}, {4, 4}, Locator}, SaveDefinitions -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/31f/31f8d6bc-f7d5-4254-965f-3f02fe648a84/58064266d747e429.png) |
| Out[8]= | 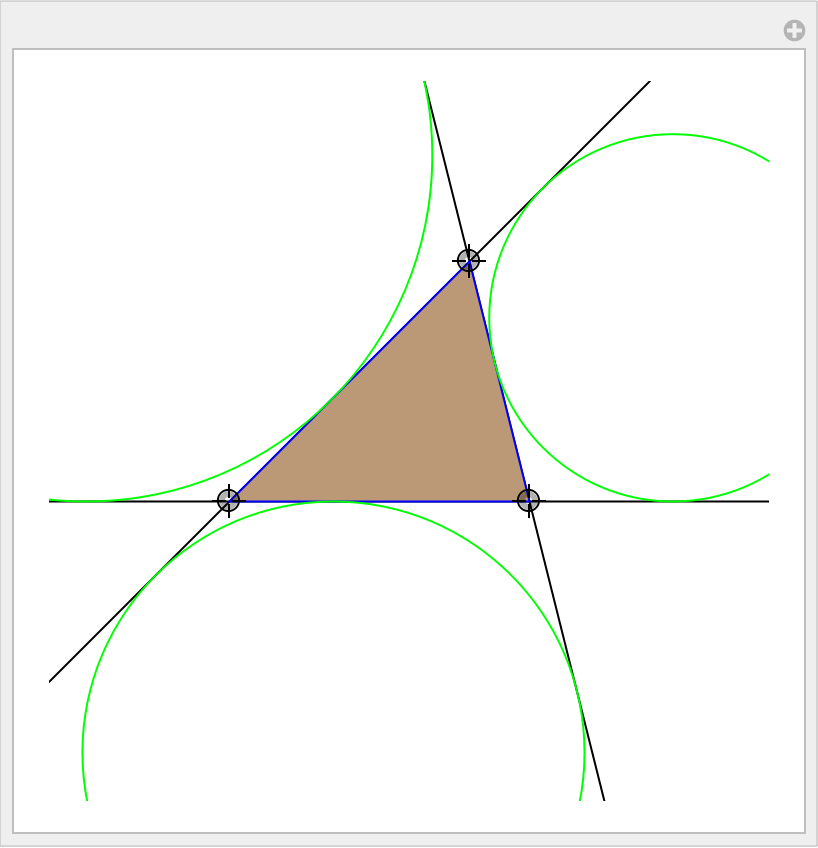 |
A triangle and its excircles:
| In[9]:= |
| Out[10]= |
Compute the center and the radius of the radical circle of the excircles:
| In[11]:= | ![sl = MapApply[EuclideanDistance, Partition[tri, 2, 1, 1]];
cent = Mean[
Map[First, MapApply[RegionIntersection, Partition[
MapApply[ResourceFunction["RadicalHyperplane"], Subsets[circs, {2}]], 2, 1, 1]]]];
rad = Sqrt[
SymmetricPolynomial[2, sl] - 2 SymmetricPolynomial[3, sl]/SymmetricPolynomial[1, sl]]/2;](https://www.wolframcloud.com/obj/resourcesystem/images/31f/31f8d6bc-f7d5-4254-965f-3f02fe648a84/40878f4186021816.png) |
Show the triangle, its excircles and the radical circle altogether:
| In[12]:= |
| Out[12]= | 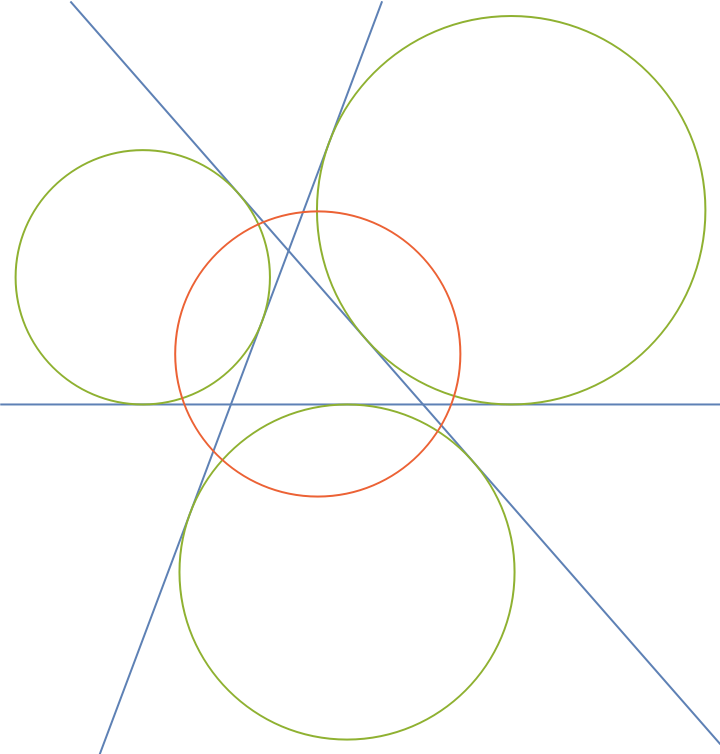 |
This work is licensed under a Creative Commons Attribution 4.0 International License