Basic Examples (6) 

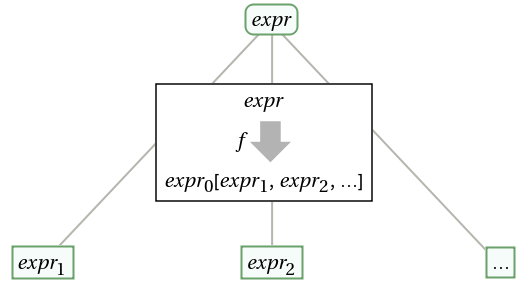
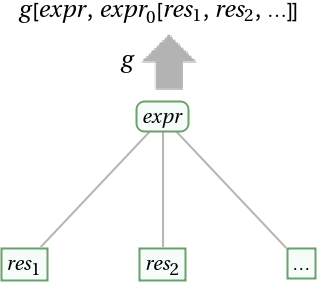
Nest a descending and an ascending operator twice:

In[1]:=

Out[1]=

Apply a descending and an ascending operator at successive levels:

In[2]:=

Out[2]=

Apply an ascending operator at the last level:

In[3]:=

Out[3]=

Construct and visualize a tree as subscripted data with highlighted leaves, adding frames around inner subtrees:

In[4]:=

Out[4]=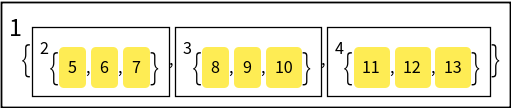

Apply descending operators to the values of an association:

In[5]:=

Out[5]=

Apply descending operators to the arguments of an arbitrary expression:

In[6]:=

Out[6]=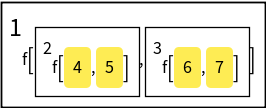

Apply successive operators at successive levels:

In[7]:=

In[8]:=

Out[8]=

In[9]:=

Out[9]=

In[10]:=

Out[10]=

Apply a descending operator f at level 1 of an array:

In[11]:=

Out[11]=

Apply Total afterward as an ascending operator at level 0:

In[12]:=

Out[12]=

Apply Total first as a descending operator at level 0 instead:

In[13]:=

Out[13]=

Scope (5) 

Apply a descending operator:

In[14]:=

Out[14]=

Apply an ascending operator:

In[15]:=

Out[15]=

Apply operators at multiple levels:

In[16]:=

Out[16]=

Apply an ascending operator at the last level:

In[17]:=

Out[17]=

Apply successive operators at successive levels:

In[18]:=

Out[18]=

Apply ascending operators to a property of the expression:

In[19]:=

Out[19]=

Atomic expressions:

In[20]:=

Out[20]=

Normal expressions:

In[21]:=

Out[21]=

In[22]:=

Out[22]=

Specify the number of additional levels:

In[23]:=

Out[23]=

Repeatedly apply descending operators until no more levels are added:

In[24]:=

Out[24]=

Apply operators without evaluating intermediate results:

In[25]:=

Out[25]=

Apply subsequent operators to the values of an association:

In[26]:=

Out[26]=

Options (2) 

Heads (2) 

By default, the operators are not applied to the heads:

In[27]:=

Out[27]=

In[28]:=

Out[28]=

In[29]:=

Out[29]=

With the option setting Heads→True, ExpressionTransform includes heads of expressions and their parts:

In[30]:=

Out[30]=

In[31]:=

Out[31]=

In[32]:=

Out[32]=

Applications (2) 

Count the number of subtrees at each level of a tree:

In[33]:=

In[34]:=

In[35]:=

Out[35]=

Create a tree of terms in a linear recurrence:

In[36]:=

Out[36]=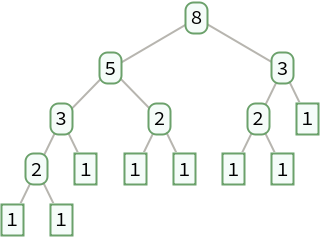

Properties and Relations (17) 

NestList gives a list of the results of successive applications of an operator f to an expression:

In[37]:=

Out[37]=

ExpressionTransform successively applies descending operators f to an expression before subsequent operators are applied at deeper levels:

In[38]:=

Out[38]=

ExpressionTransform applies subsequent operators to each part of an expression:

In[39]:=

Out[39]=

Fold gives the result of successively applying a binary operator g to the elements of a list:

In[40]:=

Out[40]=

ExpressionTransform successively applies ascending binary operators g to an expression and the result after all subsequent operators have been applied at deeper levels:

In[41]:=

Out[41]=

ExpressionTransform applies subsequent operators to each part of an expression:

In[42]:=

Out[42]=

ExpressionTransform applies subsequent operators to each part of an expression:

In[43]:=

Out[43]=

In[44]:=

Out[44]=

NestList constructs a list by successively applying an operation f to an expression:

In[45]:=

Out[45]=

Fold successively applies a binary operation g to the elements of a list:

In[46]:=

Out[46]=

ExpressionTransform constructs an expression from the top-down by successively applying descending operators f and applying ascending binary operators g to subexpressions from the bottom-up in a single traversal:

In[47]:=

Out[47]=

TreeFold[g,NestTree[f,Tree[expr,None],n,h]] is generally equivalent to ExpressionTransform[expr,f,g,n,h]:

In[48]:=

Out[48]=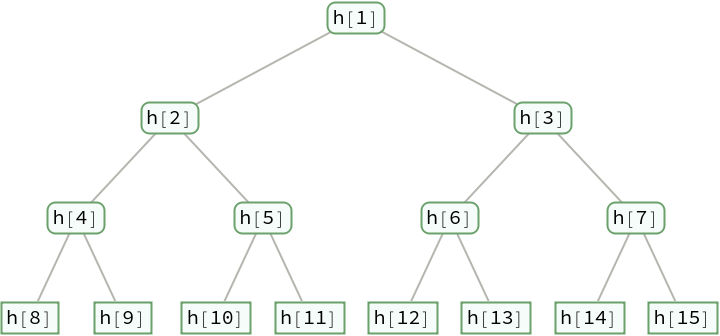

In[49]:=

Out[49]=

In[50]:=

Out[50]=

MapAll[g,expr] is generally equivalent to ExpressionTransform[expr,{},g[#2]&,g},Infinity]:

In[51]:=

Out[51]=

In[52]:=

Out[52]=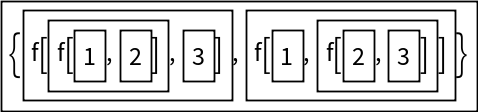

In[53]:=

Out[53]=

In ExpressionTransform, the ascending operator g takes the original expression as an argument for inner levels:

In[54]:=

Out[54]=

Apply Total as a descending operator:

In[55]:=

Out[55]=

Apply Total as an ascending operator:

In[56]:=

Out[56]=

Query applies either a descending operator or an ascending operator at each level:

In[57]:=

In[58]:=

Out[58]=

This can also be done with ExpressionTransform:

In[59]:=

Out[59]=

ExpressionTransform applies both a descending and an ascending operator at each level:

In[60]:=

Out[60]=

ExpressionTransform[expr,f,g,0] gives expr:

In[61]:=

Out[61]=

ExpressionTransform[expr,f,{…,g_-1},0] applies the operator g_-1 to expr instead:

In[62]:=

Out[62]=

ExpressionTransform[expr,f,g] gives expr if f[expr] gives an atomic expression:

In[63]:=

Out[63]=

ExpressionTransform[expr,f,{…,g_-1}] applies the operator g_-1 to expr instead:

In[64]:=

Out[64]=

ExpressionTransform[expr,f,g] applies the operator g if f[expr] gives a normal expression:

In[65]:=

Out[65]=

This is true even if f[expr] gives an expression with no arguments:

In[66]:=

Out[66]=

ExpressionTransform successively applies a descending operator f until the maximum level is reached or f returns an expression with no arguments:

In[67]:=

Out[67]=

ExpressionTransform[expr,f,g,n,h] gives the result of applying g to both h[expr] and expr₀[res₁,res₂,…], where f[expr] gives expr₀[expr₁,expr₂,…] and ExpressionTransform[expr_i,f,g,n-1,h] gives res_i:

In[68]:=

In[69]:=

Out[69]=

In[70]:=

Out[70]=

ExpressionTransform[expr,{f₀,f₁,…},{g₀,g₁,…,g_-1},n,h] gives the result of applying g₀ to both h[expr] and expr₀[res₁,res₂,…], where f₀[expr] gives expr₀[expr₁,expr₂,…] and ExpressionTransform[expr_i,{f₁,…},{g₁,…,g_-1},n-1,h] gives res_i:

In[71]:=

Out[71]=

In[72]:=

Out[72]=

ExpressionTransform[expr,{f},g,n,h] is equivalent to ExpressionTransform[expr,f,g,n,h]:

In[73]:=

Out[73]=

In[74]:=

Out[74]=

ExpressionTransform[expr,{},g,n,h] is equivalent to ExpressionTransform[Identity,g,n,h]:

In[75]:=

Out[75]=

In[76]:=

Out[76]=

ExpressionTransform[expr,f,g,n,h] is equivalent to ExpressionTransform[expr,f,{g,Identity},n,h]:

In[77]:=

Out[77]=

In[78]:=

Out[78]=

ExpressionTransform[expr,f,{g},n,h] is equivalent to ExpressionTransform[expr,f,{#2&,g},n,h]:

In[79]:=

Out[79]=

In[80]:=

Out[80]=

ExpressionTransform[expr,f,{},n,h] is equivalent to ExpressionTransform[expr,f,{#2&,Identity},n,h]:

In[81]:=

Out[81]=

In[82]:=

Out[82]=

ExpressionTransform[expr,{},{},Infinity] is generally equivalent to expr:

In[83]:=

Out[83]=

Neat Examples (5) 

Construct the 3^rd-step Sierpiński triangle:

In[84]:=

Out[84]=

Construct the 3^rd-step Cantor set:

In[85]:=

Out[85]=

Define functions to compute branches of a fractal:

In[86]:=

In[87]:=

In[88]:=

Construct a graphical image of the lines connecting the constructed points in the 0^th- through 7^th steps:

In[89]:=

Out[89]=

In[90]:=

Out[90]=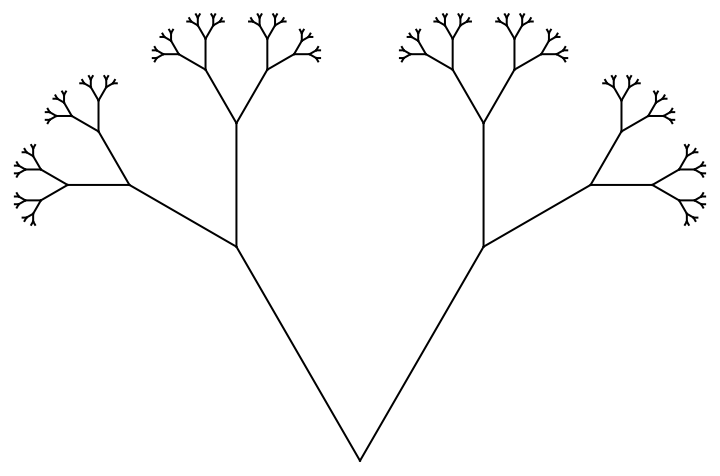

Define a function that divides a list with two or more elements into a left half and a right half:

In[91]:=

Define a function that merges two sorted lists giving a sorted list:

In[92]:=

In[93]:=

Perform a merge sort on a random list:

In[94]:=

Out[94]=

In[95]:=

Out[95]=

Define a function that divides a non-empty list into the list of elements less than or equal to a pivot element and the list of elements greater than the pivot element:

In[96]:=

In[97]:=

Define a function that merges the results of sorting these lists:

In[98]:=

Perform a quick sort on a random list:

In[99]:=

Out[99]=

In[100]:=

Out[100]=