Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Convert an expression to a pure function by specifying which symbols should be used as input arguments
ResourceFunction["ExpressionToFunction"][expr,var1,var2,…] returns Function[{var1,var2,…},expr]. | |
ResourceFunction["ExpressionToFunction"][expr,…,{vari,1,vari,2,…},…] bundles {vari,1,vari,2,…} together in one function slot as a vector argument. | |
ResourceFunction["ExpressionToFunction"][expr,varspec1→index1,varspec2→index2,…] binds variables specified by varspeci to Slot[indexi]. |
| Attributes | None | attributes that the pure function should have |
| Evaluated | False | whether to evaluate the function body |
Create a function from a simple polynomial:
| In[1]:= |
| Out[1]= |
Evaluate the polynomial at a given value:
| In[2]:= |
| Out[2]= |
Convert a multivariate PDF to a function:
| In[3]:= |
| Out[3]= | 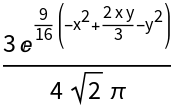 |
| In[4]:= |
| Out[4]= | 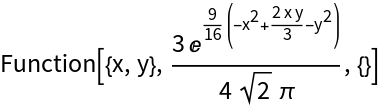 |
| In[5]:= |
| Out[5]= |
Bind x and y to the first slot of the function as a vector:
| In[6]:= |
| Out[6]= | 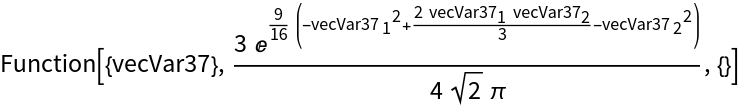 |
| In[7]:= |
| Out[7]= |
Bind arguments to keys in an Association:
| In[8]:= |
| Out[8]= |
| In[9]:= |
| Out[9]= |
Bind multiple symbols to a single slot:
| In[10]:= |
| Out[10]= |
| In[11]:= |
| Out[11]= |
| In[12]:= |
| Out[12]= |
Combine named slots with positional slots:
| In[13]:= |
| Out[13]= |
| In[14]:= |
| Out[14]= |
Use the Attributes option to return a function that holds its arguments:
| In[15]:= |
| Out[15]= |
| In[16]:= |
| Out[16]= |
| In[17]:= |
| Out[17]= |
| In[18]:= |
| Out[18]= |
By default, the function body remains unevaluated:
| In[19]:= |
| Out[19]= |
Use Evaluated → True to evaluate the PDF:
| In[20]:= |
| Out[20]= | 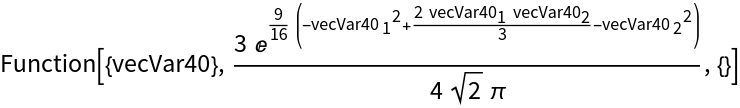 |
When x has a value, using Evaluate directly on the first argument gives the wrong result:
| In[21]:= |
| Out[21]= |
Use Evaluated → True to Block x while the body is being evaluated:
| In[22]:= |
| Out[22]= | 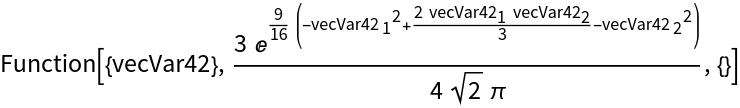 |
Group x and y together as a vector argument and map over a list of points:
| In[23]:= | ![pdfVectorFun = ResourceFunction["ExpressionToFunction"][
PDF[BinormalDistribution[1/3], {x, y}], {x, y}, Evaluated -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/bd7/bd773914-a5be-4cf8-9e22-197b7b8abdd4/524e092d85fdc1f5.png) |
| Out[23]= | 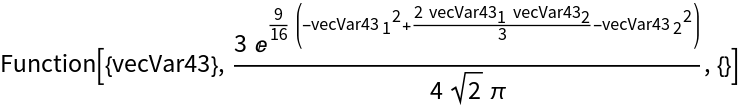 |
| In[24]:= |
| In[25]:= |
| In[26]:= |
| Out[26]= | 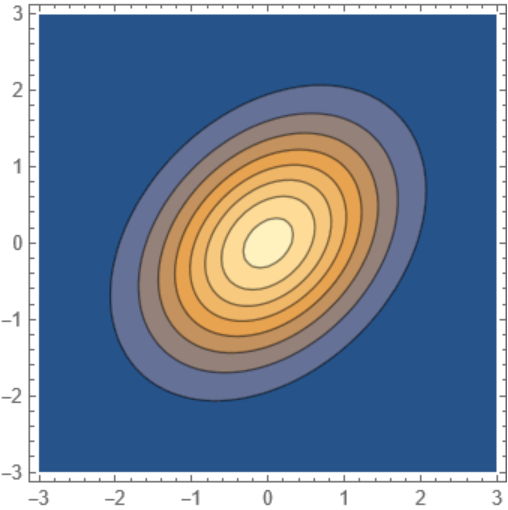 |
Add a parameter of the PDF as an argument:
| In[27]:= | ![parameterizedPDF = ResourceFunction["ExpressionToFunction"][
PDF[BinormalDistribution[\[Rho]], {x, y}],
{x, y},
\[Rho],
Evaluated -> True
]](https://www.wolframcloud.com/obj/resourcesystem/images/bd7/bd773914-a5be-4cf8-9e22-197b7b8abdd4/40e56be4f255c8b8.png) |
| Out[27]= |  |
| In[28]:= |
| Out[28]= |
Convert the solution of a differential equation to a function:
| In[29]:= |
| Out[29]= |
| In[30]:= |
| Out[30]= |
| In[31]:= |
| Out[31]= |
Represent the function at parameter value a=10 with OperatorApplied, then map over a range of x values:
| In[32]:= | ![AssociationMap[
OperatorApplied[dSolveFun][10],
Range[0, 10, 0.1]
] // ListPlot](https://www.wolframcloud.com/obj/resourcesystem/images/bd7/bd773914-a5be-4cf8-9e22-197b7b8abdd4/2f4989e8e9c005f1.png) |
| Out[32]= | 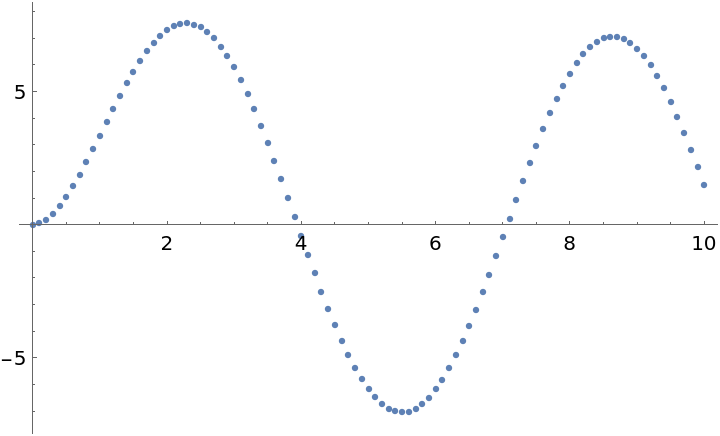 |
The resource function ExpressionToFunctionOperator is the operator form of ExpressionToFunction:
| In[33]:= |
| Out[33]= |
| In[34]:= |
| Out[34]= |
Note, in particular, that both functions hold the expression that's being transformed into a function unless Evaluated→True is used:
| In[35]:= |
| Out[35]= |
| In[36]:= |
| Out[36]= |
With evaluation of the expression:
| In[37]:= |
| Out[37]= | 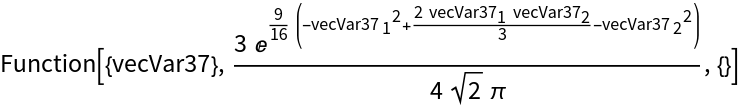 |
| In[38]:= |
| Out[38]= | 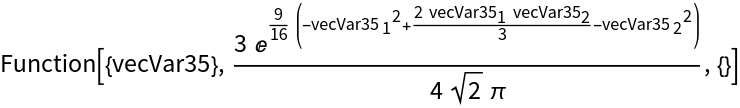 |
ExpressionToFunction is meant for expressions that do not already contain functions and may malfunction for such expressions if the replacement variables exist inside such functions:
| In[39]:= |
| Out[39]= |
| In[40]:= |
| Out[40]= |
The correct result would be:
| In[41]:= | ![ReleaseHold[
Hold[Function[#1 + x]@y] /. {x -> x0, y -> y0}
]](https://www.wolframcloud.com/obj/resourcesystem/images/bd7/bd773914-a5be-4cf8-9e22-197b7b8abdd4/033b21fd914cf93a.png) |
| Out[41]= |
The problem can sometimes be avoided by evaluating the inner function away:
| In[42]:= |
| Out[42]= |
Wolfram Language 11.3 (March 2018) or above
This work is licensed under a Creative Commons Attribution 4.0 International License