Basic Examples (3)
Find the marks for a sparse ruler of length 9:
Check that all differences are covered:
Find the marks for a sparse ruler of length 57:
Check that the ruler is complete, i.e. that all differences are covered:
Show the intervals between marks in the full form of a length-396 ruler:
Split the differences:
Make a series of lists from the compact form of a length-396 ruler:
Show the compact form:
Verify that the compact form from the previous result has length 396:
Show the full form for a length-396 ruler:
Scope (6)
Show the marks for the first 51 rulers:
Show the excess values for the first 51 rulers:
Count the number of marks for a length-58 ruler in full form or compact form:
The excess of a ruler with length L and M marks is  :
:
An excess-01 ruler has an excess of 0 or 1:
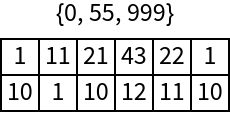
A list of some rulers with a single mark less than those generated by this function:
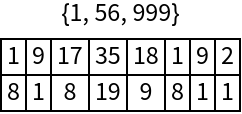
Show the length-999 ruler with one less mark:
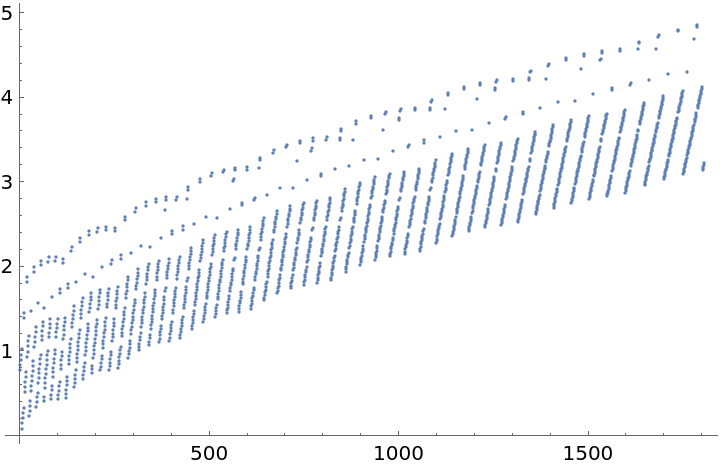
Show how the Leech upper bound for the number of marks in a complete ruler compares to the number of marks in function-generated rulers:
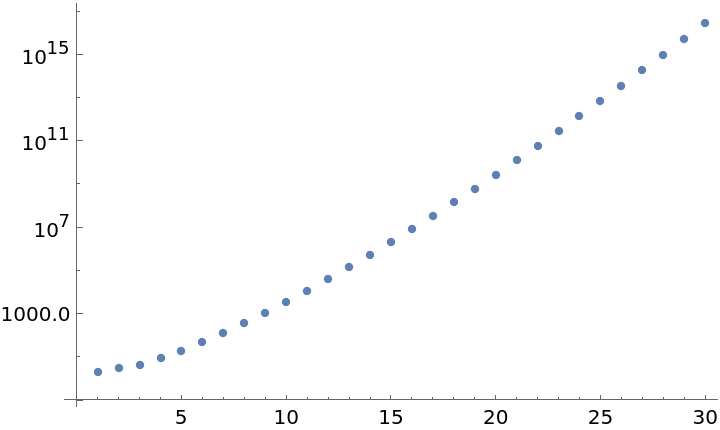
Generate rulers of length n! and plot the number of marks:
Possible Issues (2)
Show the default shortened form for a length-googol ruler:
Show the number of marks in a length-googol ruler:
Showing the full form of a googol-length ruler is not recommended.
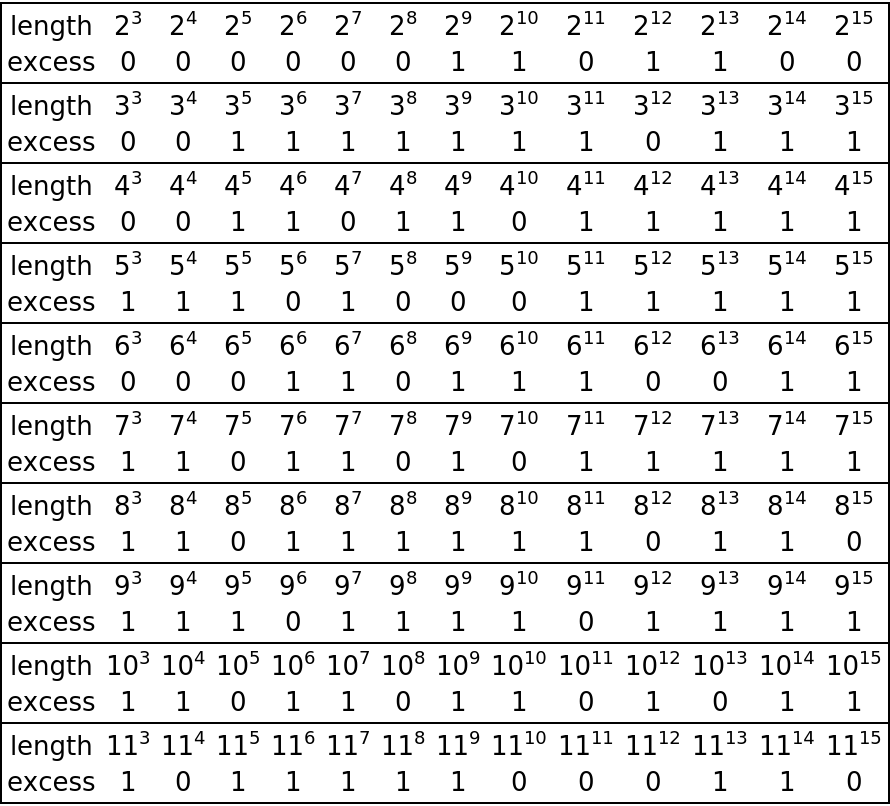
Neat Examples (3)
Generate reasonable rulers for various integer powers and calculate their excess:
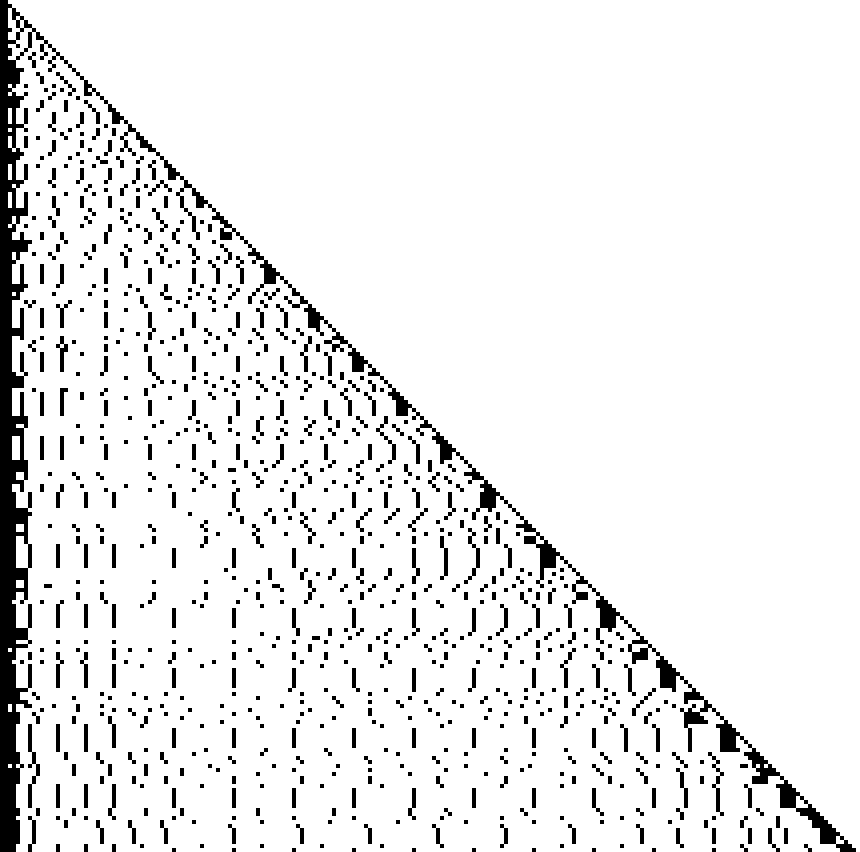
All rulers to length 213 are minimal. Show a pixel representation of these sparse rulers:
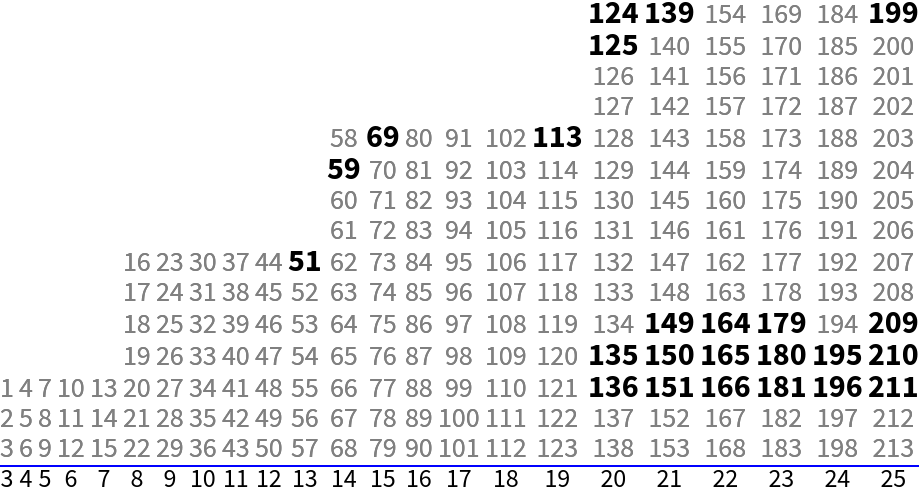
The maximal length for a given number of marks is usually a Wichmann value:
Arrange lengths in columns ending in Wichmann values and bold the lengths with excess 1:

![]() :
:![length = 999;
ruler = ResourceFunction["Excess01Ruler"][length];
marks = Total[Last[ruler]] + 1;
excess = marks - Round[Sqrt[3 length + 9/4]];
Column[{{excess, marks, length}, Grid[ruler, Frame -> All]}, Alignment -> Center]](https://www.wolframcloud.com/obj/resourcesystem/images/55c/55c596a2-013c-4c19-b932-dc72c394ab98/48d6262acdd1cd75.png)
![ruler = betterRulers[[208]];
length = Dot @@ ruler;
marks = Total[Last[ruler]] + 1;
excess = marks - Round[Sqrt[3 length + 9/4]];
Column[{{excess, marks, length}, Grid[ruler, Frame -> All]}, Alignment -> Center]](https://www.wolframcloud.com/obj/resourcesystem/images/55c/55c596a2-013c-4c19-b932-dc72c394ab98/72def79bac4455b7.png)

![Text@Grid[Flatten[Table[Transpose[Prepend[
Table[{base^ToString[n], Total[ResourceFunction["Excess01Ruler"][base^n][[2]]] + 1 - Round[Sqrt[3 base^n + 9/4]]}, {n, 3, 15}], {"length", "excess"}]],
{base, 2, 11}], 1], Dividers -> {True, {{True, False}}}]](https://www.wolframcloud.com/obj/resourcesystem/images/55c/55c596a2-013c-4c19-b932-dc72c394ab98/6418d9c1433157c6.png)
![ArrayPlot[Table[PadRight[ReplacePart[Table[0, {n + 1}],
({# + 1} & /@ ResourceFunction["Excess01Ruler"][n, "Full"]) -> 1],
215], {n, 1, 213}], PixelConstrained -> 2, Frame -> False]](https://www.wolframcloud.com/obj/resourcesystem/images/55c/55c596a2-013c-4c19-b932-dc72c394ab98/585bf9dbbe2f41a8.png)
![Grid[Append[
Transpose[
Table[PadLeft[
Take[Style[
If[Length[ResourceFunction["Excess01Ruler"][#, "Full"]] - Round[Sqrt[3 # + 9/4]] == 1, Style[#, Black, Bold, 16], Style[#, Gray, 14]]] & /@ Range[213],
{WichmannValues[[n]] + 1, WichmannValues[[n + 1]]}], 15, ""], {n, 24 - 1}]], Range[3, 25]], Spacings -> {.2, .2}, Dividers -> {False, -2 -> Blue}]](https://www.wolframcloud.com/obj/resourcesystem/images/55c/55c596a2-013c-4c19-b932-dc72c394ab98/4288d541aef5ed8b.png)