Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Compute the evolutoid of a curve
ResourceFunction["EvolutoidCurve"][c,θ,t] computes the evolutoid with angle θ of the curve c defined with respect to the variable t. |
Parametric equations for an ellipse:
| In[1]:= |
Compute the evolutoid of an ellipse with angle equal to GoldenAngle:
| In[2]:= |
| Out[2]= |  |
Plot the ellipse and its evolutoid:
| In[3]:= | ![\[Alpha] = ellipse[Sqrt[2], 1, t];
\[Epsilon] = ResourceFunction["EvolutoidCurve"][\[Alpha], GoldenAngle, t];
ParametricPlot[Evaluate[{\[Alpha], \[Epsilon]}], {t, 0, 2 \[Pi]}]](https://www.wolframcloud.com/obj/resourcesystem/images/573/57332975-4012-424c-a1b1-e9e1dc4c1e52/44ecfdd0db8afc5b.png) |
| Out[3]= | 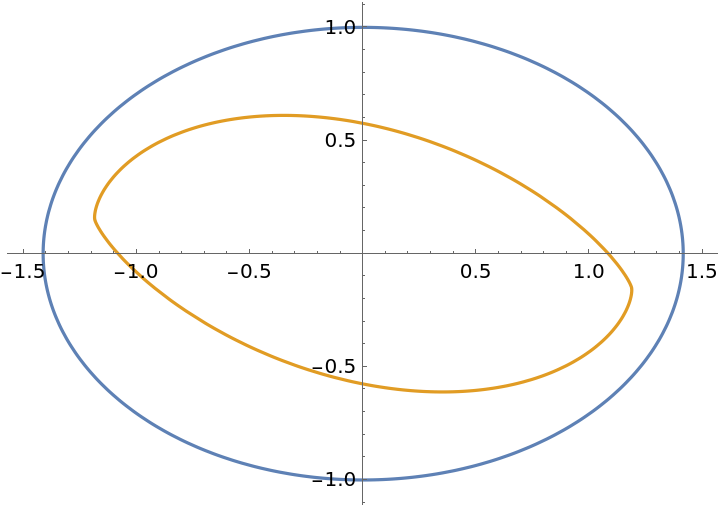 |
When ![]() , EvolutoidCurve is the same as the resource function EvoluteCurve:
, EvolutoidCurve is the same as the resource function EvoluteCurve:
| In[4]:= |
| Out[4]= |
| In[5]:= |
| Out[5]= |
Demonstrate the effect of changing θ in EvolutoidCurve:
| In[6]:= | ![Manipulate[
ParametricPlot[
Evaluate[{cc[t], ResourceFunction["EvolutoidCurve"][cc[t], \[Theta], t]}], {t, 0, 2 \[Pi]}], {{\[Theta], \[Pi]/2}, 0, \[Pi]}, SaveDefinitions -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/573/57332975-4012-424c-a1b1-e9e1dc4c1e52/7040396668210f00.png) |
| Out[6]= | 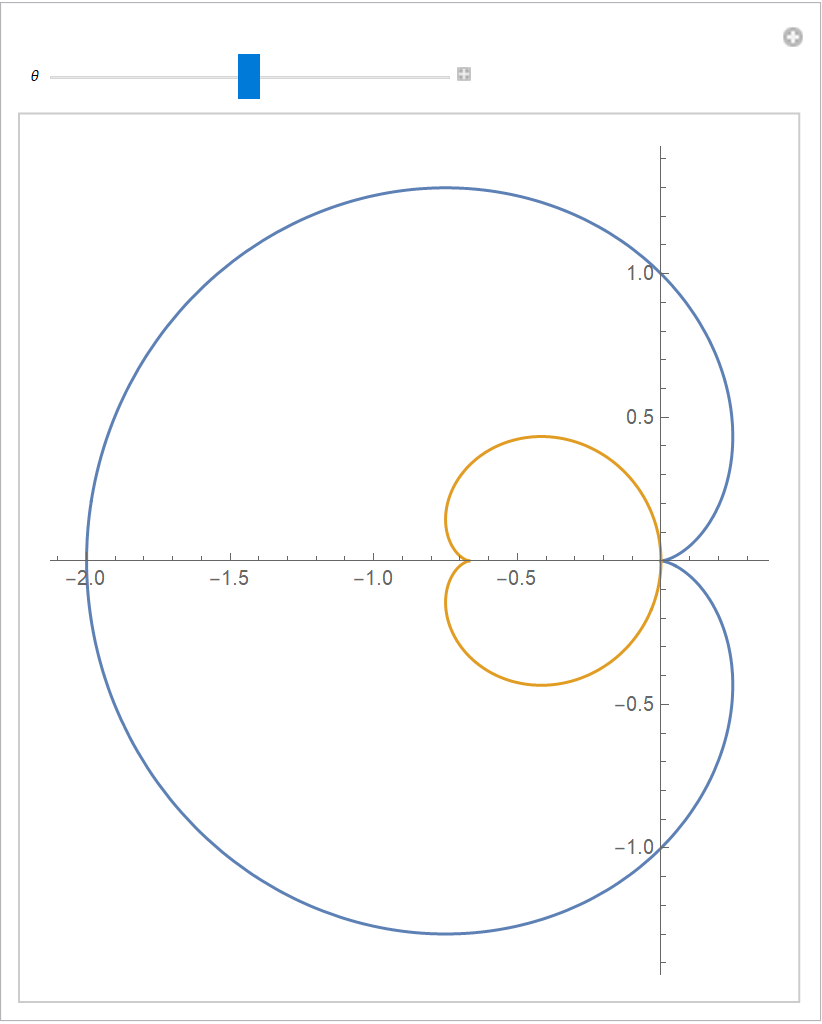 |
This work is licensed under a Creative Commons Attribution 4.0 International License