Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Get even permutations of a list
ResourceFunction["EvenPermutations"][list] returns the even permutations of list. | |
ResourceFunction["EvenPermutations"][list,count] returns count even permutations of list. |
The even permutations of {1,2,3,4}:
| In[1]:= |
| Out[1]= |
The even permutations of {2,1,3,4}:
| In[2]:= |
| Out[2]= |
The even permutations of an odd permutation have signature -1:
| In[3]:= |
| Out[3]= |
Ten even permutations of {1,…,15}:
| In[4]:= |
| Out[4]= |  |
For a list of 12 items, rather than returning 12!/2 = 239500800 items, a sampling of even permutations is given:
| In[5]:= |
| Out[5]= |  |
Use even permutations to embed an icosahedron within a tetrahedron:
| In[6]:= | ![p = {0, 1/2, 1/4 (3 - Sqrt[5]), 1/4 (-1 + Sqrt[5])};
tet = {{-1, 1, 1}, {1, -1, 1}, {1, 1, -1}, {-1, -1, -1}};
ico = RootReduce[
ResourceFunction["Areal"][tet, #] & /@ ResourceFunction["EvenPermutations"][p]];
edge1 = ResourceFunction["FindExtraordinaryLines"][Join[ico, tet]];
edge2 = Select[Subsets[Range[12], {2}], Quiet@RootReduce[EuclideanDistance @@ ico[[#]]] == 3 - Sqrt[5] &];
Graphics3D[{Tube[Join[ico, tet][[#]], .06] & /@ Join[edge1, edge2], Opacity[.5], Simplex[tet]}, Boxed -> False, SphericalRegion -> True]](https://www.wolframcloud.com/obj/resourcesystem/images/351/351a706a-23d2-47ad-bbcc-7e96f1713b05/7c5d0a611f9b5c67.png) |
| Out[6]= | 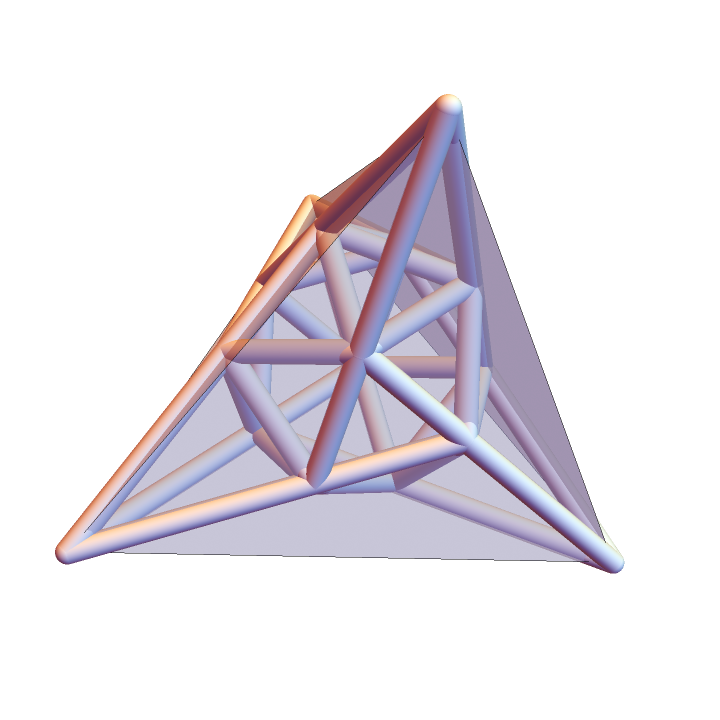 |
This work is licensed under a Creative Commons Attribution 4.0 International License