Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Add edges to a graph to make it Eulerian
ResourceFunction["EulerizeGraph"][graph] adds edges to a connected graph to make it Eulerian. |
Create the bridges of Königsberg graph:
| In[1]:= | ![islands = {\[ScriptCapitalT], \[ScriptCapitalL], \[ScriptCapitalM], \[ScriptCapitalR]};
bridges = {\[ScriptCapitalL] \[UndirectedEdge] \[ScriptCapitalM], \[ScriptCapitalL] \[UndirectedEdge] \[ScriptCapitalM], \[ScriptCapitalT] \[UndirectedEdge] \[ScriptCapitalM], \[ScriptCapitalT] \[UndirectedEdge] \[ScriptCapitalM], \[ScriptCapitalM] \[UndirectedEdge] \[ScriptCapitalR], \[ScriptCapitalR] \[UndirectedEdge] \[ScriptCapitalT], \[ScriptCapitalR] \[UndirectedEdge] \[ScriptCapitalL]};
bridgesOfKonigsbergSystem = Graph[islands, bridges, VertexLabels -> "Name"]](https://www.wolframcloud.com/obj/resourcesystem/images/ab0/ab0af3c7-e965-45ba-a8b7-1a6d07f595ce/139f48dceceead5c.png) |
| Out[3]= | 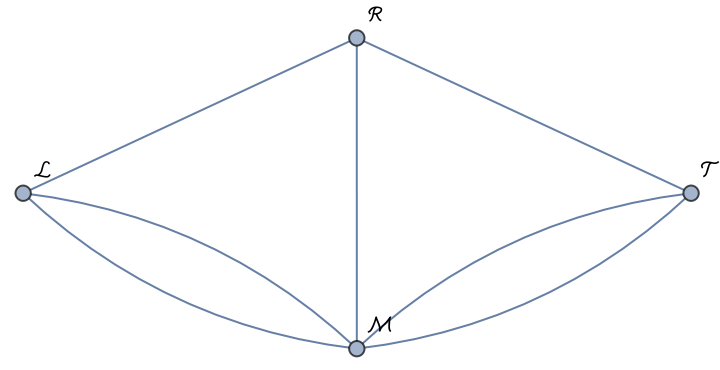 |
Eulerize the Königsberg graph:
| In[4]:= |
| Out[4]= |  |
Eulerize the graph corresponding to the modern-day bridges of Königsberg (some of the original bridges are no longer present):
| In[5]:= | ![Konigsburg2022 = Graph[islands, {\[ScriptCapitalL] \[UndirectedEdge] \[ScriptCapitalR], \[ScriptCapitalR] \[UndirectedEdge] \[ScriptCapitalM], \[ScriptCapitalT] \[UndirectedEdge] \[ScriptCapitalM], \[ScriptCapitalM] \[UndirectedEdge] \[ScriptCapitalL], \[ScriptCapitalR] \[UndirectedEdge] \[ScriptCapitalT]}, VertexLabels -> "Name"];
Row[{Konigsburg2022, ResourceFunction["EulerizeGraph"][Konigsburg2022]}]](https://www.wolframcloud.com/obj/resourcesystem/images/ab0/ab0af3c7-e965-45ba-a8b7-1a6d07f595ce/29f4f64005e0940e.png) |
| Out[6]= | 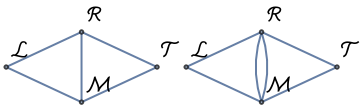 |
Show the Pappus graph and its Eulerized counterpart:
| In[7]:= |
| Out[8]= | 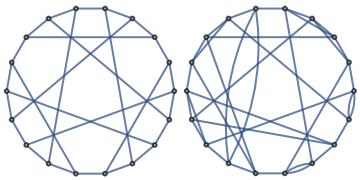 |
If a graph is already Eulerian, the graph remains unchanged:
| In[9]:= |
| Out[9]= |  |
Check that it is Eulerian:
| In[10]:= |
| Out[10]= |
Check that the original and Eulerized graphs are identical:
| In[11]:= |
| Out[11]= |
This work is licensed under a Creative Commons Attribution 4.0 International License