Wolfram Function Repository
Instant-use add-on functions for the Wolfram Language
Function Repository Resource:
Construct a Pascal-like triangular graph representing Eulerian numbers
ResourceFunction["EulerianNumberTriangle"][n] constructs a triangle that encodes the Eulerian numbers arranged in n+1 layers with edge weights. |
Generate an Eulerian number triangle with 6 levels:
| In[1]:= |
| Out[1]= | 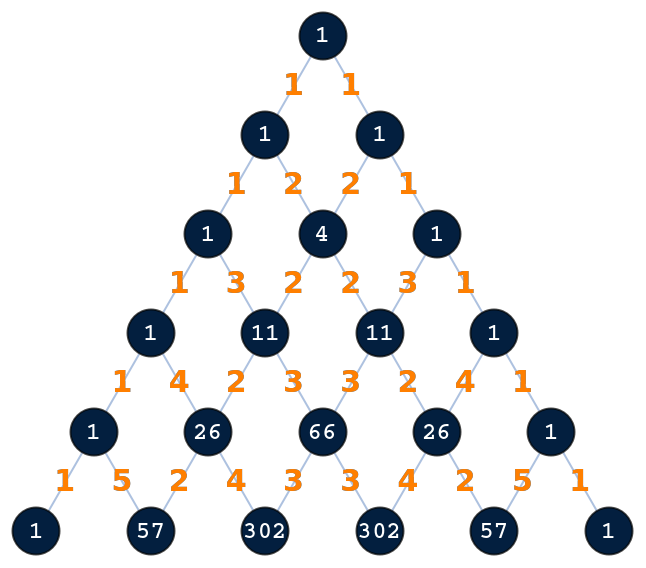 |
Mouse over to display Eulerian numbers larger than 1000:
| In[2]:= |
| Out[2]= | 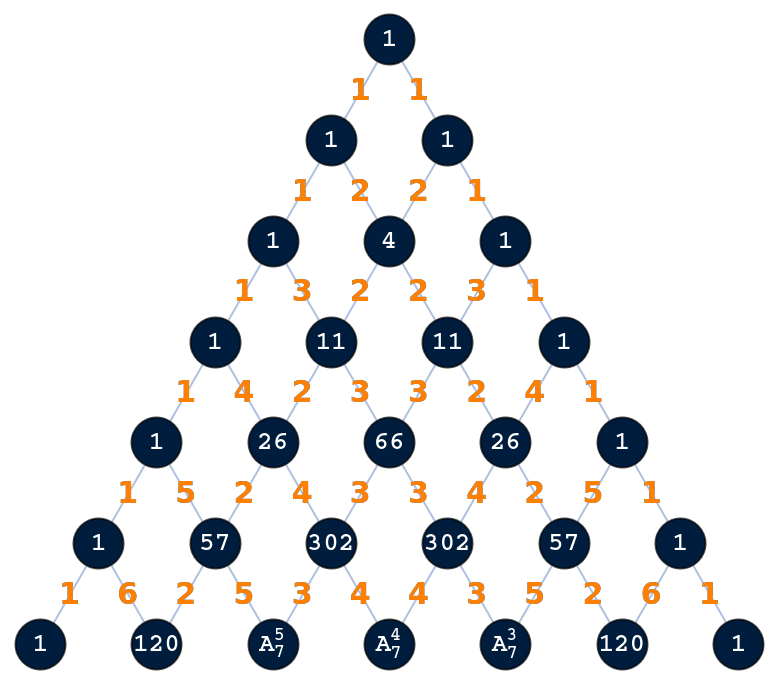 |
EulerianNumberTriangle returns a weighed Graph object:
| In[3]:= |
| Out[4]= |
Each value in the node is the weighted sum of the parent items, for example, 26 = 4·1+11·2:
| In[5]:= |
| Out[5]= | 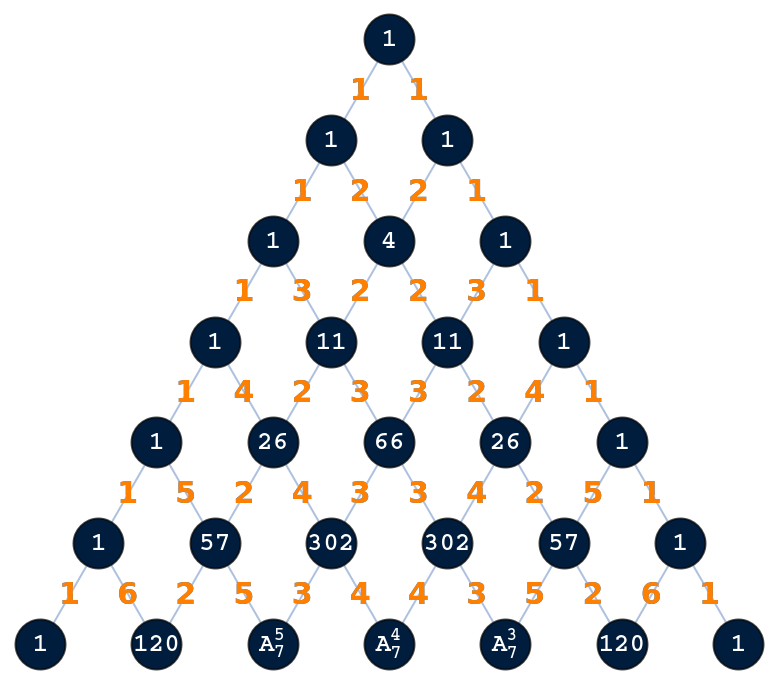 |
The sum of all elements in the n th row is Factorial[n], for example the 6th row:
| In[6]:= |
| Out[6]= |
Or the 7th row:
| In[7]:= |
| Out[7]= |
Retrieve all numerical values from the graph nodes:
| In[8]:= | ![n = 12;
g = ResourceFunction["EulerianNumberTriangle"][n];
With[{vtx = ResourceFunction["EulerianNumber"] @@@ VertexList[g]}, Take[vtx, Binomial[#, 2] + {1, #}] & /@ Range[n]] // Column](https://www.wolframcloud.com/obj/resourcesystem/images/8ec/8ec9e39b-c21d-422a-b97c-47ba824f7370/72559b7e85bd75f0.png) |
| Out[9]= |  |
Maximum visualization depth is 41 layers with n=40. For larger value the function returns unevaluated:
| In[10]:= |
| Out[10]= |
The ArrayPlot of the adjacency matrix for an Eulerian number triangle:
| In[11]:= |
| In[12]:= |
| Out[12]= |  |
All eigenvalues are real because of the matrix itself is real and symmetric:
| In[13]:= |
| Out[13]= |  |
This work is licensed under a Creative Commons Attribution 4.0 International License