Basic Examples (2) 

Find all integers m such that ϕ(m)=1000:

In[1]:=

Out[1]=

Check:

In[2]:=

Out[2]=

Scope (2) 

Find all 6535 integers m such that ϕ(m)=10²⁰:

In[3]:=

Out[3]=

In[4]:=

Out[4]=

In[5]:=

Out[5]=

Verify that these are the correct solutions:

In[6]:=

Out[6]=

It takes only a fraction of second to find all solution for the numbers below on a modern computer:

In[7]:=

Out[7]=

In[8]:=

Out[8]=

Properties and Relations (2) 

EulerPhiInverse returns an empty list for all odd integer except 1:

In[9]:=

Out[9]=

List non-totients:

In[10]:=

Out[10]=

Show that non-totients have no preimage under Euler's totient function:

In[11]:=

Out[11]=

Possible Issues (2) 

EulerPhiInverse only handles positive integers. Otherwise, it returns unevaluated:

In[12]:=

Out[12]=

The number of solutions may grow rapidly for those inputs with prime factors p such that p-1 is highly composite:

In[13]:=

Out[13]=

Increase the second argument to get all solutions for x such that EulerPhi[x]=10²⁸:

In[14]:=

Out[14]=

Neat Examples (3) 

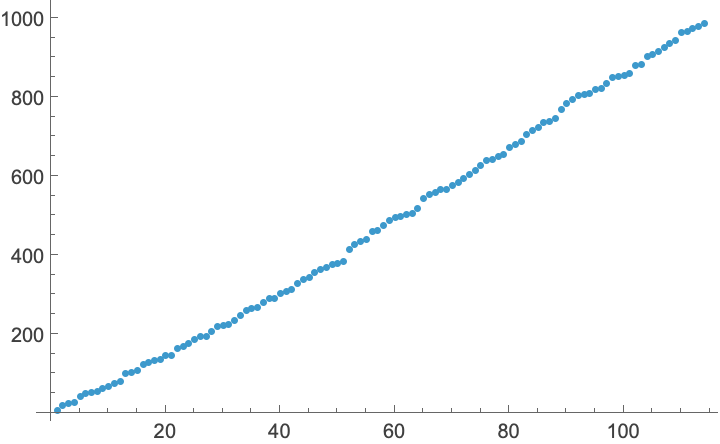
Numbers k such that EulerPhi[x]=k has exactly 2 solutions (OEIS A007366):

In[15]:=

Out[16]=

In[17]:=

Out[17]=

Visualize the data:

In[18]:=

Out[18]=

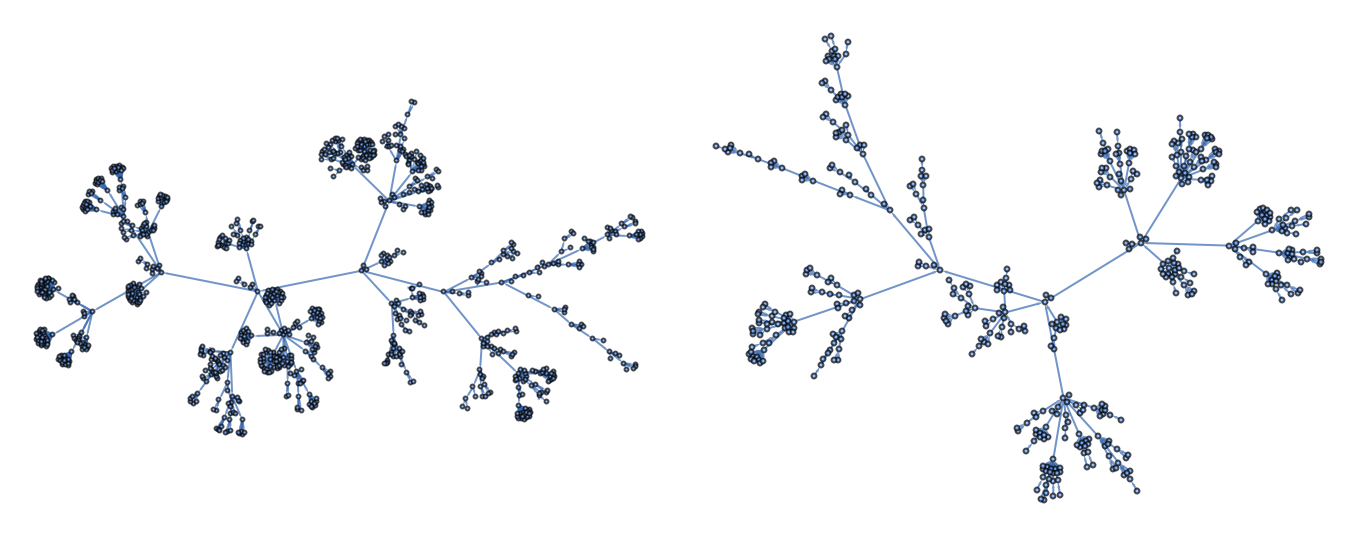
A pair of dual graph: two integers m and n are connected if ϕ(m)=n on the left and ϕ^-1(m)=n on the right:

In[19]:=

Out[20]=

The graph on the left hand side seems denser than the right because the inverse of ϕ is a multivalued function:

In[21]:=

Out[21]=

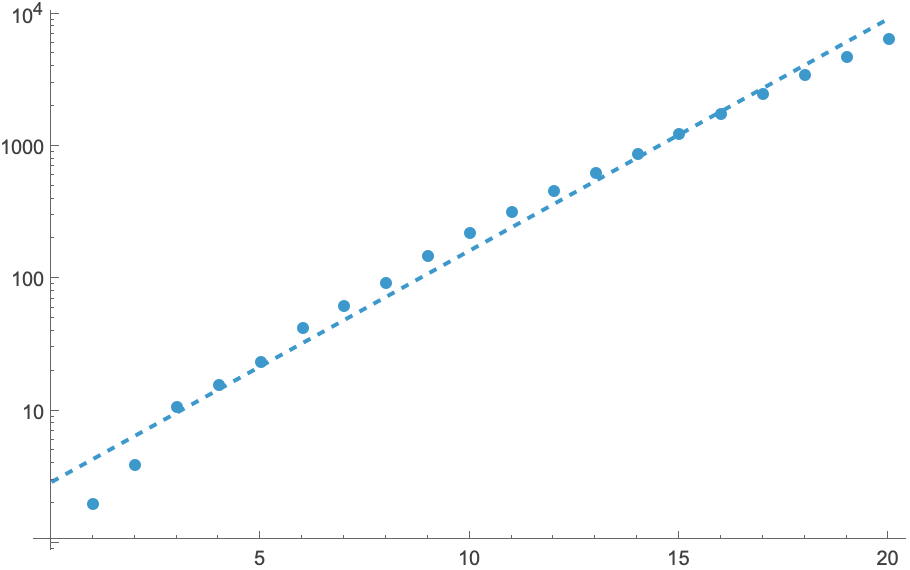
Number of integers k such that EulerPhi[k]=n (OEIS A072074):

In[22]:=

Out[23]=

In[24]:=

Out[24]=

Plot the data and its logarithm approximation:

In[25]:=

In[26]:=

Out[26]=